跳转至

TENET - A Framework for Modeling Tensor Dataflow Based on Relation-centric Notation

Info

Link: arxiv

摘要&结论

目的：建立精确性能模型，评估不同数据流性能

动机：基于计算(compute-centric)和基于数据(data-centric)的数据流表达能力差，导致优化机会受限，性能模型不准确

内容：使用基于关系(relation-centric)的记号形式化表达张量计算中的数据流；使用关系刻画硬件数据流、PE互联、数据分配

优势：

  1. 具有更强的表现力：使用复杂的反射变换
    • 可识别更复杂的硬件数据流，具有更大的数据流设计空间和更多张量基准
  2. 支持更精确的性能估计：数据重用、延迟、能耗
    • 方法：使用整数集结构和运算对关系计数

引言

空间架构(spatial architectures)：

  • 概念：并行计算架构，使用多个处理单元在空间分布上同时处理多个任务
  • 构成：计算单元(PE)阵列 + 片上缓存(scratchpad memory) + PE片上互联
  • 性质：存在大量硬件数据流变体

硬件数据流(hardware dataflow)：

  • 张量操作表示：循环嵌套
  • 硬件数据流表示：
    1. 循环实例在PE阵列上的分配
    2. 循环实例在PE上的执行顺序
  • 硬件数据流决定PE利用率、数据访存模式和片上带宽需求
  • 问题：缺乏形式化表达
    • 理想的形式化表达应满足：
      1. 系统地覆盖完整的数据流设计空间
      2. 促进简单而准确的性能建模
    • 现有形式化表达方案：基于计算，基于数据
      • 问题：
        1. 表达能力差，只能表达硬件数据流的一个子集
          • 无法表达倾斜循环/张量数据流（需仿射变换以进行循环实例到空间架构的映射）
        2. 无法支持精确地性能分析
          • 基于计算的模型未对数据迁移重用直接建模
          • 基于数据的模型在张量维度未显式指定时无法精确计算指标（基于数据的模型通过计算关于参数的多项式对指标进行建模）

TENET：对空间架构上张量应用程序的数据流进行建模的框架

  • 核心：基于关系的表示(relation-centric notation)
  • 关系：可表为pair的集合，使用整数集合运算进行计算
    1. 循环实例与执行计算的PE之间的关系（循环实例在哪里执行 where）
    2. 循环实例与其在PE中的执行顺序的关系（循环实例何时执行 when）
    3. PE和对应分配的张量元素的关系（张量元素在何时何地被访问 where & when）
    4. PE和互联网络的关系（张量元素如何遍历PE，如脉动阵列 how）
  • 优势：
    1. 仅使用关系刻画复杂硬件数据流
    2. 完整的数据流设计空间
      • 数据流 + 数据分配 + 内部连接的关系表示 => 完整硬件数据流设计空间
    3. 支持对各种重要性能指标进行简单而准确的建模
      • 基本量：总体数据量、重用数据量以及需要在 PE 和片上缓存之间传输的最小数据量
      • 使用基本量推导其余硬件指标
  • 作用：可评估多种硬件指标：数据重用、延迟、PE通信带宽和片上内存带宽

背景

空间架构

空间架构：

  • 概念：具有一系列PE、PE间互联和内存层级的一类架构
    • PE：具有ALU用于执行特定计算，寄存器堆用于数据存储
    • PE间互联：增加数据重用机会，降低带宽要求
      • 数据重用：时间重用，空间重用
        • 时间重用：同一数据在不同周期使用（数据 -> CC1,...,n）
        • 空间重用：同一数据在不同PE使用（数据 -> PE1,...,n）
    • 内存层级：3层
      1. PE寄存器级
      2. 片上缓存器级
      3. 片外存储器级
  • 模型假设：
    1. ALU具有执行1次乘积累加(MAC)操作的能力
    2. 相邻PE通过片上互联进行的数据传输需要1周期

硬件数据流：

  • 概念：特定张量应用在某个空间架构上的实现
    • 张量应用通常使用循环嵌套表示
  • 表示：
    1. 循环实例在哪个PE上执行
    2. 循环实例在PE上的执行顺序

循环 编译优化记号

循环下标\(\vec n=(i,j,\cdots)\)

计算实例\(S[\vec n]\)：某个具体循环下标下所执行计算语句

循环迭代空间\(D_S=\set{S[\vec n]|\vec n=(i,j,\cdots)}\)：所有计算实例的集合

张量空间\(D_F=\set{F[\vec{n'}]}\)：\(|\vec n'|\)阶张量张成的空间

张量映射函数（访问函数）\(A_{S,F}=\set{S[\vec n]\to F[\vec f]}\)：循环迭代空间到张量空间的映射，表示一个计算实例的执行具体需要用到哪些张量

例：矩阵乘法

计算实例\(S[\vec n]:Y[i,j]+=A[i,k]\times B[k,j],\vec n=(i,j,k)\)

张量空间：\(D_A=\set{A[\vec{n'}]|\vec{n'}=(i,k)}\)，\(D_B=\set{B[\vec{n''}]|\vec{n''}=(k,j)}\)

映射函数：\(A_{D_S\to(D_A,D_B)}=\set{S[i,j,k]\to(A[i,k],B[k,j])}\)

现有数据流记号的局限性

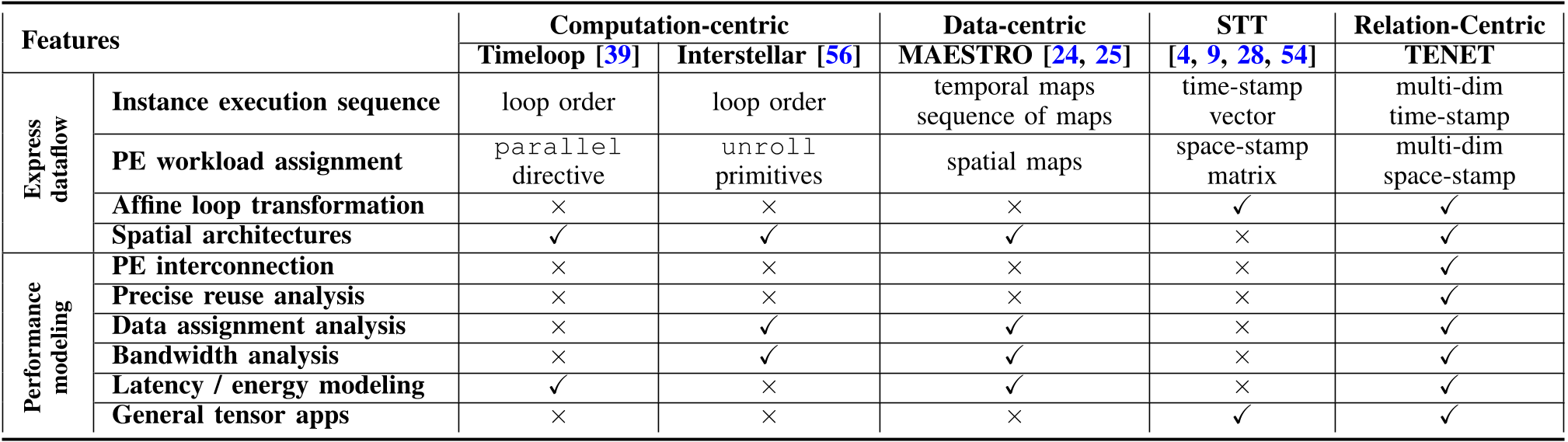
image.png

数据流表示：

  • 基于计算：
    • 循环转移指令：重排、阻塞、并行
    • 表示：
      • 执行顺序：循环顺序
      • 负载分配：需额外的parallel指令
    • 优势：以命令式风格灵活地描述计算的执行过程
  • 基于数据：
    • 数据映射指令：时间 / 空间映射、数据移动顺序
    • 表示：
      • 执行顺序：Temporal Map指令描述数据在某一维度上跨时间戳移动（同一PE）
      • 负载分配：Spatial Map指令 （不同PE）
    • 优势：易于计算数据重用
    • 问题：需手写指令，复杂数据流难处理
  • 时空变换(STT)：
    • 将循环映射到脉动阵列上
    • 问题：
      • 不具备性能模型
      • 不支持非脉动阵列架构

局限性：表达能力 & 性能建模能力

  1. 无法包含完整的数据流设计空间：
    • 仅能表达矩形数据流，斜数据流需要做仿射变换
    • 斜数据流须手动对原有张量应用进行转化，导致性能分析困难
  2. 仅粗粒度的对数据重用进行分析：
    • 仅使用简单多项式计算数据流动
    • 本质：仅能对部分张量的数据流进行建模

模型架构

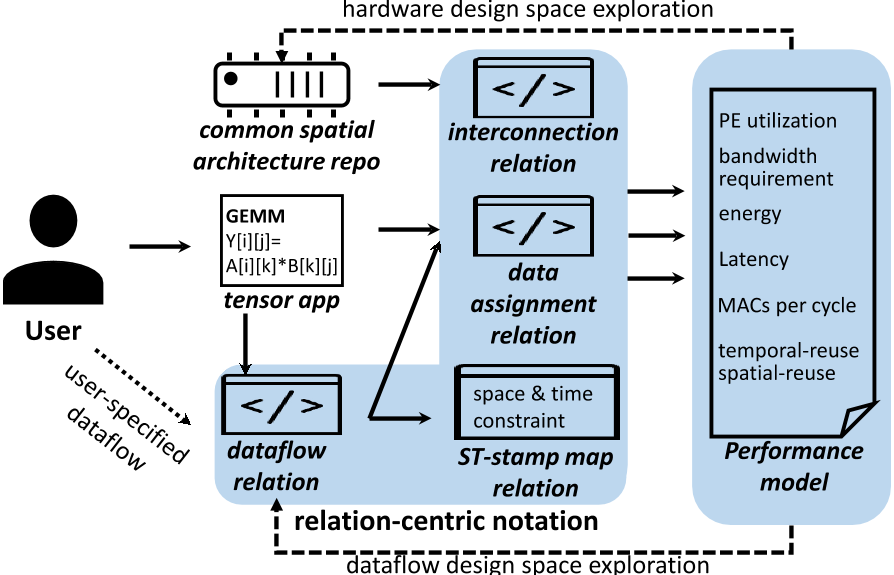
image.png

  1. 输入C语言编写的张量操作，硬件描述
  2. 生成基于关系的表示：数据流、数据分配、互联、时空戳映射关系
    • 数据流关系：将每个循环实例与PE相关联
      • 方法：设计空间自动探索(DSE), 手动指定
    • 数据分配关系：结合张量操作的访问函数和数据流关系得到
    • 互联关系：描述PE间连接方式，从架构中推出
    • 时空戳关系：针对特定的数据流，计算多钟时空戳映射关系，用于性能估计
  3. 计算关键性能指标
  4. 提供常用空间架构仓库

基于关系的记号

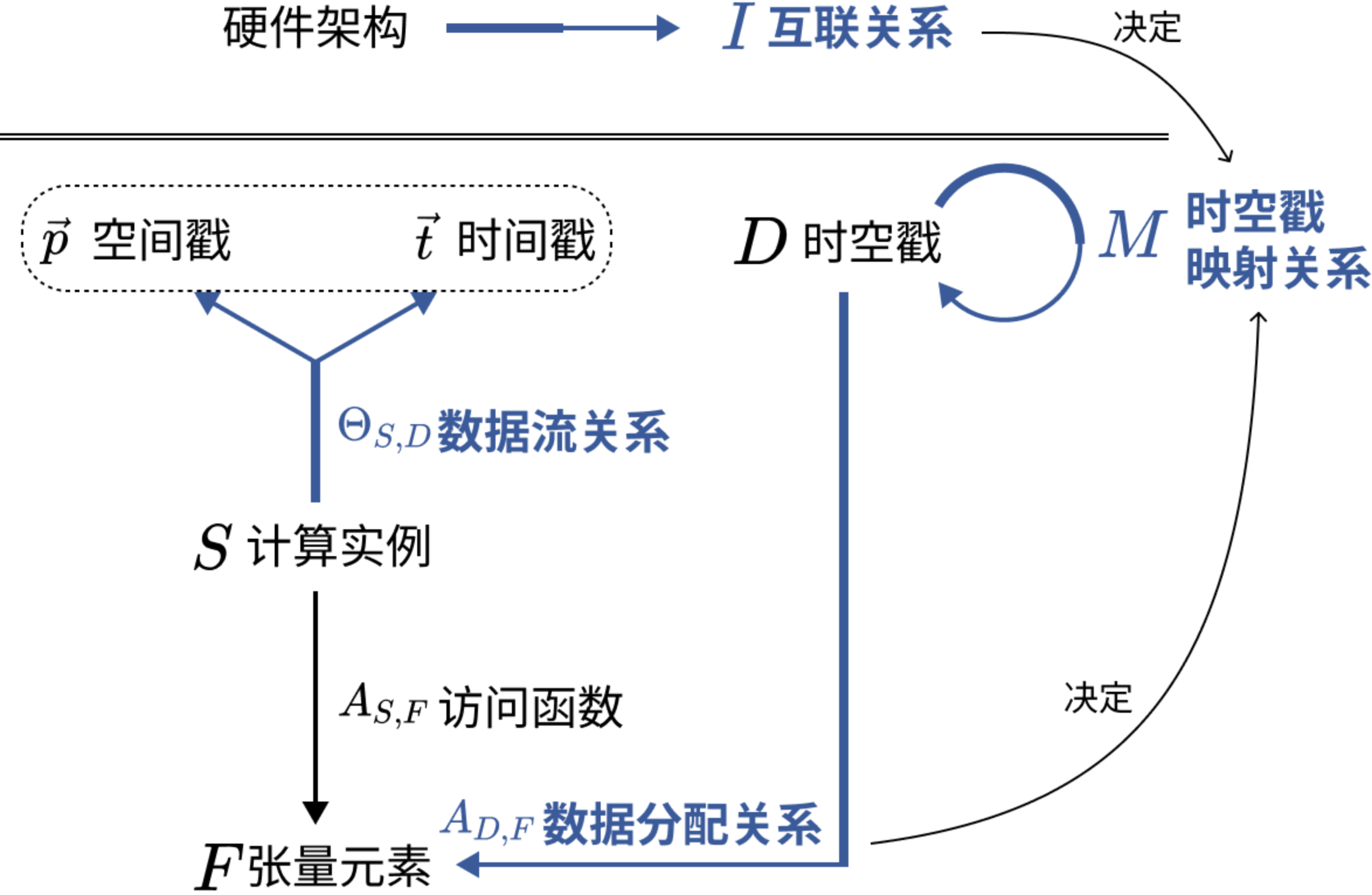
image.png

4类关系：

  1. 数据流关系：计算实例 -> 时空戳
    • 戳：由于排序、放置的依据
      • 空间戳：执行循环实例的PE的坐标
      • 时间戳：决定PE内循环实例的执行顺序
        • 循环实例的执行顺序由时间戳的字典序决定
    • 表示：\(\Theta_{S,D}=\set{S[\vec n]\to(PE[\vec p]\ |\ T[\vec t])},S[\vec n]\in D_S\)
      • 时空戳\(\vec p,\vec t\)为循环下标\(\vec n\)的仿射变换（线性映射）
        • 空间戳维度与PE阵列拓扑一致
        • 当迭代空间大于PE阵列时，时间戳为多维
          • 准仿射变换，引入除法、取模运算
        • 时空戳的每一维都是循环下标的线性组合
      • 具体计算过程表示：带入具体的时空约束，解得循环实例的时空分配
    • 数据流设计空间：
      • 假设：
        1. PE只有一个MAC单元
        2. PE阵列为2D
        3. 数据顺序流动
          • 基于数据的记号size = offset = 1
          • 基于关系的记号变换系数为1
      • 基于数据：\(O(n!C_n^2)\)
        • \(n\)条原语全排列，由于PE阵列为2D，有两条SpatialMap
      • 基于关系：\(O(2^{n^2})\)
        • n维到n维线性映射，表示为\(n\times n\)矩阵，由于系数为1，故\(a_{ij}\in\set{0,1}\)，共\(2^{n^2}\)种矩阵
  2. 数据分配关系：时空戳 -> 张量
    • 定义：\(A_{D,F}=\Theta_{S,D}^{-1}A_{S,F}=\set{(PE[\vec p]\ |\ T[\vec t])\to F[\vec f]}\)
    • 作用：发现时空重用机会
  3. 互联关系：PE1 -> PE2
    • 表示：\(I_{PE_1,PE_2}=\set{PE[\vec{p_1}]\to PE[\vec{p_2}]}:c_1,\cdots,c_k\)
      • \(\vec p\)：拓扑坐标，\(c_i\)：拓扑约束
    • 作用：描述可能的数据流动方式
      • 互联：数据重用
      • 不互联：通过片上缓存读取
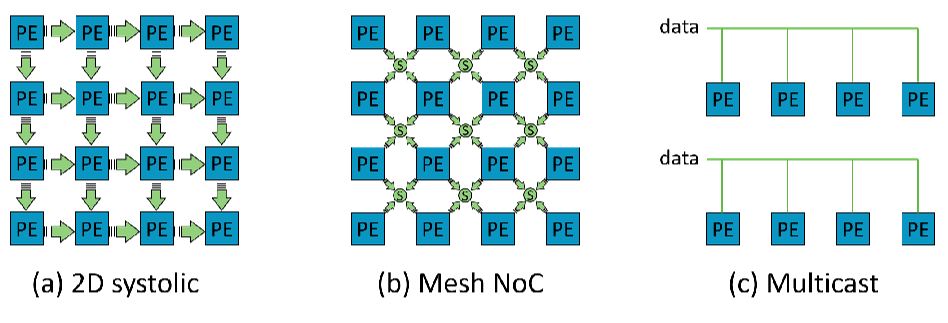
    • 常见片连拓扑：记\(I=\set{PE[i,j]\to PE[i',j']}\) image.png
      • 2D脉动阵列：\(i'=i,j'=j+1\lor i'=i+1,j'=j\)
      • 片上网络：\(|i'-i|\leqslant1\land |j-j'|\leqslant1\)
      • 1D多广播：\(|i'-i|\leqslant k\)
  4. 时空映射关系：由数据分配、互联关系决定，通过关联不同时空戳，对连续时空戳空间的硬件行为进行建模
    • 表示：\(M_{D,D'}=\set{(PE[\vec{p_1}]\ |\ T[\vec{t_1}])\to(PE[\vec{p_2}]\ |\ T[\vec{t_2}])}\)
    • 作用：计算性能指标
      • 例：识别数据重用
        • 令PE不变：时间重用
        • 令PE相邻：空间重用

例：矩阵乘法 (GEMM算子)

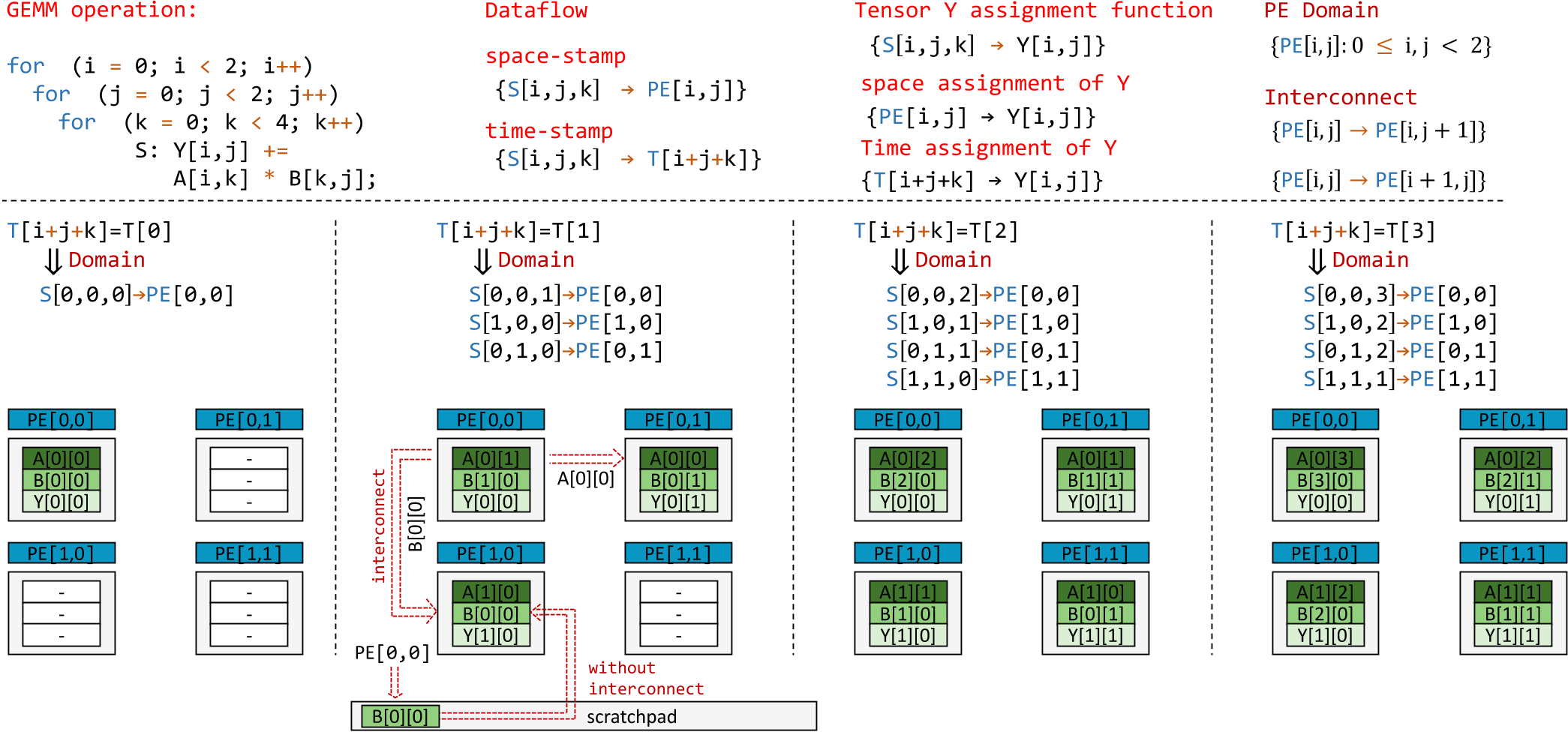
image.png

  • 数据流关系：\(\Theta_{S,D}=\set{S[i,j,k]\to(PE[i,j]\ |\ T[i+j+k])}\)
    • \(t=1\)时数据分布：即\(T[1]\)，令\(i+j+k=1\)，s.t. \(0\leqslant i,j<2,0\leqslant k<4\)，解得\([i,j,k]=[0,0,1],[1,0,0],[0,1,0]\)
    • 当循环迭代空间大于PE阵列(\(n\times n\))时，表示为\(\Theta_{S,D}=\set{S[i,j,k]\to(PE[i\bmod n,j\bmod n])\ |\ T[i/n,j/n,(i\bmod n+j\bmod n+k)]}\)
  • 数据到张量\(Y\)的分配关系：\(A_{D,F_Y}=\set{(PE[i,j]\ |\ T[i+j+k])\to Y[i,j]}\)
  • 互联关系：\(\set{PE[i,j]\to PE[i,j+1]},\set{PE[i,j]\to PE[i+1,j]}\)
  • 时空戳映射：
    • \((PE[0,0]\ |\ T[0])\to(PE[0,0]\ |\ T[1])\)
      • \((PE[0,0]\ |\ T[0])\to Y[0,0],(PE[0,0]\ |\ T[1])\to Y[0,0]\)
      • \(Y[0,0]\)在\(PE[0,0]\)

性能模型

性能指标：数据传输量，数据重用，延迟，能量(?)

数据量

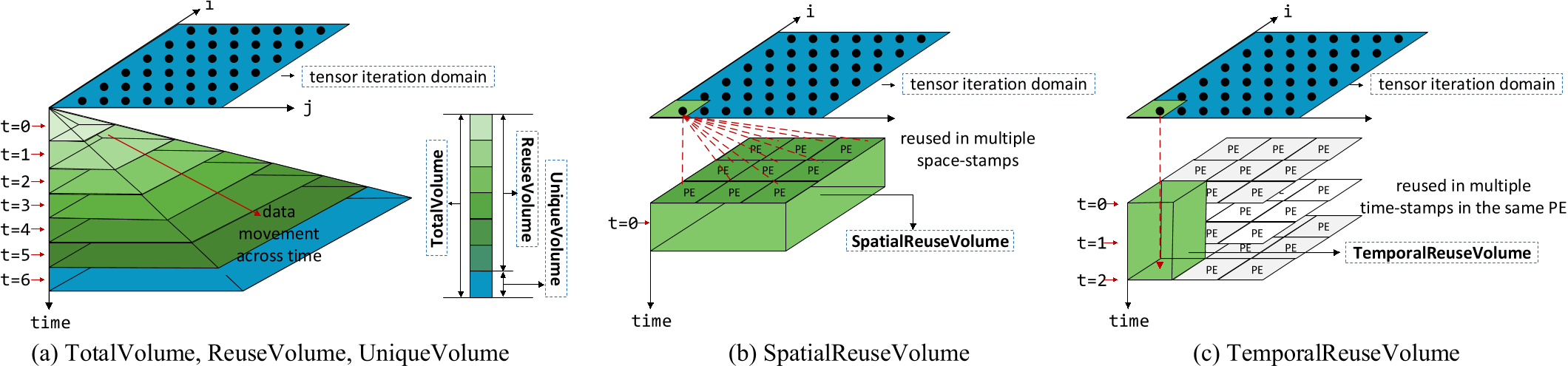
image.png

  • 表示：sum(·) 集合基数
  • 4种数据量：
    1. 总数据量：所有时空戳对某张量访问的总次数
      • 计算：\(\text{TotalVolumn}=\text{sum}(A_{D,F})\)
      • 性质：PE与片上缓存间所需传输的最大数据量
    2. 重用数据量：跨多个时空戳的重用数据量，即相邻时空戳的重叠数据量（第一次出现不算重用）
      • 计算：\(\text{ReuseVolumn}=\text{sum}(A_{D,F}\cup A_{D',F})=\text{sum}(A_{D,F}\cup M_{D,D'}^{-1}A_{D,F})\)
      • \(M_{D,D'}\)：相邻时空戳
        • 空间重用量：跨不同空间戳数据重用量
          • \(M_{D,D'}\)由片联拓扑限制（仅满足片联拓扑约束的PE对空间重用量有贡献）
        • 时间重用量：同一PE内跨不同时间戳数据重用量（限制同一PE避免与空间重用量重叠）
          • 同一PE，\(M_{D,D'}\)由时间间隔限制（在某一时间间隔内的数据可被重用）
            • 脉动阵列：假设时间间隔为1的数据可重用（PE间传输需要一个时钟周期），设时间间隔为1
            • 多广播：设时间间隔为0（数据通过wire进行重用）
        • 关系：\(\text{ReuseVolumn}=\text{SpatialReuseVolumn}+\text{TemporalReuseVolumn}\)
    3. 唯一数据量：访问不同张量数据的数量（不能从相邻时空戳中获得的数据），即新加入的数据总量
      • 计算：\(\text{UniqueVolumn}=\text{TotalVolumn}-\text{ReuseVolumn}\)
      • 性质：PE与片上缓存间所需传输的最小数据量
    4. 重用因子：一个数据平均重用次数
      • 计算：\(\text{ReuseFactor}=\text{TotalVolumn}/\text{UniqueVolumn}\)

例：矩阵乘法中的张量A

时空戳 PE[0,0] PE[0,1] PE[1,0] PE[1,1]
t=0 A[0][0]
t=1 A[0][1] A[0][0] A[1][0]
t=2 A[0][2] A[0][1] A[1][1] A[1][0]
t=3 A[0][3] A[0][2] A[1][2] A[1][1]
  • 总数据量：\(1+3+4+4=12\)
  • 重用数据量：\(1+2+2=5\)
  • 唯一数据量：\(1+2+2+2=7\)
  • 重用因子：\(12/7=1.714\)

延迟与带宽模型

模型假设：数据流延迟 = \(\max\{\)通信延迟，计算延迟\(\}\)

  • 通信延迟：片上缓存和PE寄存器间数据传输引起（当PE可从自身或相邻PE获取数据时，无需从片上缓存获取数据）
    • 估计：\(\text{Delay}_\text{read}=\dfrac{\text{UniqueVolumn(Input)}}{\text{bandwidth}},\text{Delay}_\text{write}=\dfrac{\text{UniqueVolumn(Ouput)}}{\text{bandwidth}}\)
      • 其中带宽为片上缓存带宽（每秒能传输的数据量）
  • 计算延迟：计算实例的总量和可用PE数之比（一个计算实例即一次MAC运算）
    • 估计：\(\text{Delay}_{\text{compute}}=\dfrac{\text{sum}(D_S)}{\text{Util}_{\text{PE}}\times\text{PE size}}\)
      • 其中\(\text{Util}_{PE}\)为PE平均利用率
  • 带宽要求：数据传输速度需与计算速度相匹配，在计算所需的时间内数据需传输到位
    • PE间带宽：\(IBW=\dfrac{\text{SpatialReuseVolumn}}{\text{Delay}_{\text{compute}}}\)
      • PE间传输的为空间重用数据
    • PE、片上缓存间带宽：\(SBW=\dfrac{\text{UniqueVolumn}}{\text{Delay}_\text{compute}}\)
      • 唯一数据量代表PE、片上缓存间传输的数据总量

实验

Benchmark：

  • 2D-CONV：\(Y(k,ox,oy)\text{+=}A(c,ox+rx,oy+ry)B(k,c,rx,ry)\)
  • GEMM：\(Y(i,j)\text{+=}A(i,k)B(k,j)\)
  • MTTKRP：\(Y(i,j)\text{+=}A(i,k,l)B(k,j)C(l,j)\)
  • MMc：\(Y(i,j)\text{+=}A(i,k)B(k,l)C(l,j)\)
  • Jacobi-2D：\(Y(i,j)\text{+=}(A(i,j)+A(i-1,j)+A(i,j-1)+A(i+1,j)+A(i,j+1))/5\)
  • 现实应用：
    • GoogLeNet
    • MobileNet
    • ALS
    • Transformer

数据流记号：(空间戳 - P | 时间戳 - T)

  • 仿射变换：将所有维度名放在一起
  • 特殊符号：fl(·) 下取整 % 取模

数据流比较

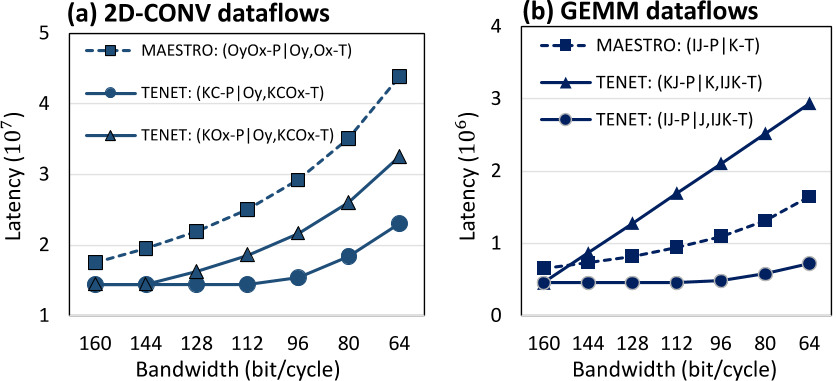
image.png

结论：

  • 基于关系的表示法表达能力比基于数据的表示法强
  • 从而基于关系的表示法为寻找更优数据流提供了机会（TENET能建模比基于数据的MAESTRO得到的最优数据流更优的数据流）
    • 原因：基于关系的表示法识别到了更加复杂的数据流

建模速度比较

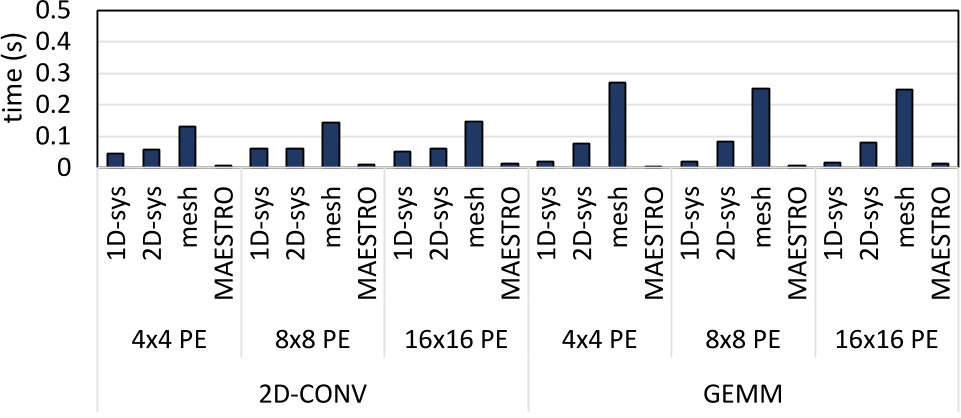
image.png

结论：

  • TENET将数据流建模视作线性规划问题，考虑更多架构细节
  • MAESTRO仅使用简单多项式进行性能计算，快而不准
  • PE连接方式越复杂，建模时间越长；对PE大小不敏感

设计空间探索：由于TENET表达能力强，相应的设计空间更大

  • 通过限制数据空间流动、分配关系对设计空间进行剪枝
    • 性质：在仿射变换下，数据流动始终沿直线
    • 操作：
      1. 根据PE互联枚举数据移动方式
      2. 枚举边界上PE的可能数据分配

性能指标评估

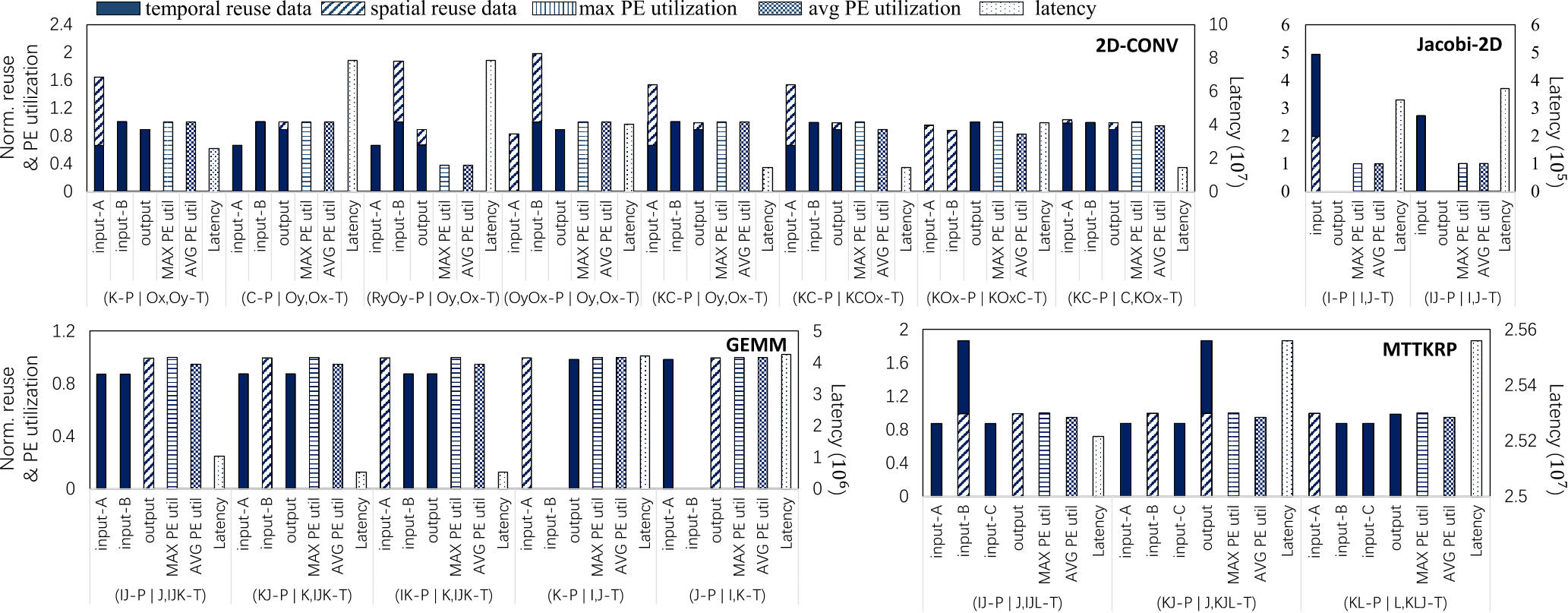
image.png

结论：好的数据流应同时具有高PE利用率和数据重用

  • 高数据重用不是低延迟的必要条件
    • \((R_YO_Y-P\ |\ O_Y,O_X-T)\)数据流由于\(R_Y\)维度与PE阵列大小不匹配，导致PE利用率低，导致高延迟
    • \((C-P\ |\ O_Y,O_X-T)\)数据流由于输入\(A\)具有低重用，导致载入数据具有高延迟
  • 2D空间戳可展现更多重用机会
  • TENET可分别捕获时空重用

带宽分析

互联建模：同一周期多广播

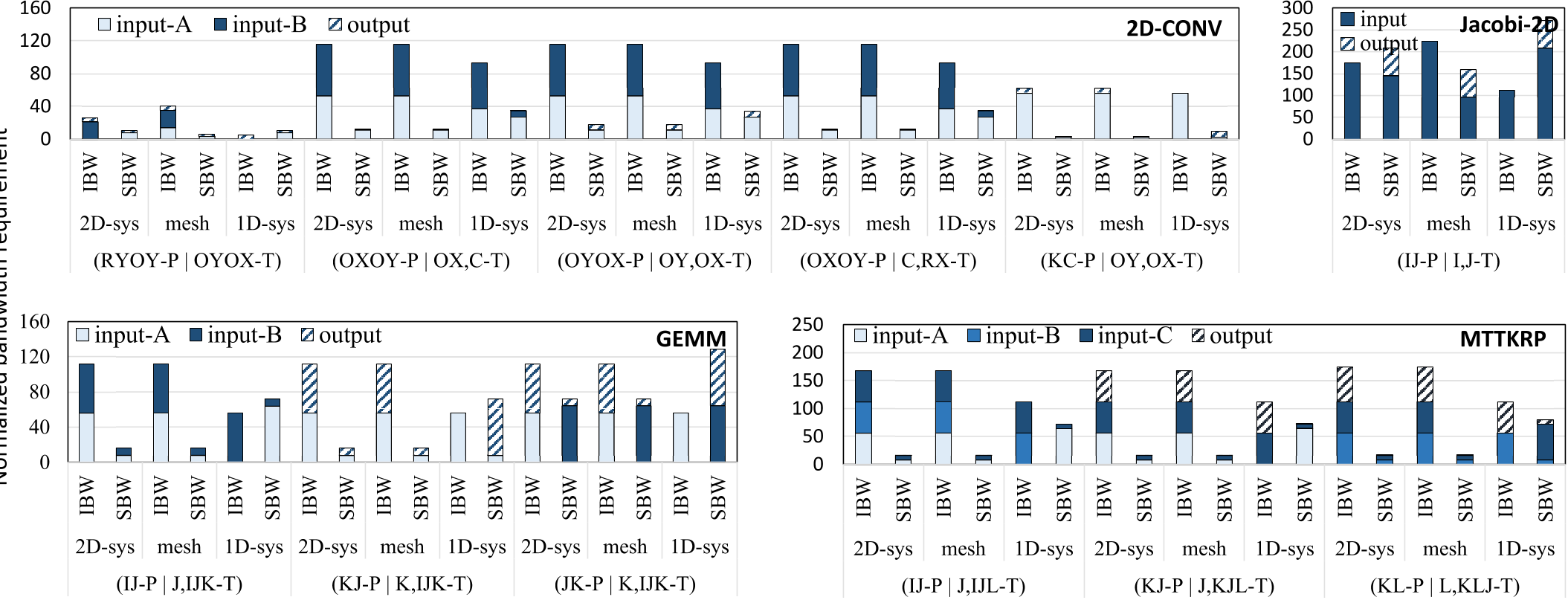
image.png

结论：增加互联PE数量不是降低片上缓存带宽需求的必要条件

  • 不同架构对同一数据流带宽要求类似
    • 张量应用通常具有规则的计算和数据访问，鲜少有长距离跨PE通信
  • 当数据流变化时，带宽需求来自不同的张量
  • 数据重用需和硬件架构相匹配
    • \((R_YO_Y-P\ |\ O_Y,O_X-T)\) 2D-CONV, Jacobi-2D数据流，mesh拓扑IBW大于其它架构，SBW小于其它架构，该数据流发掘了对角数据重用，而脉动阵列不支持
    • \((R_YO_Y-P\ |\ O_Y,O_X-T)\) 2D-CONV数据流，1D脉动阵列的IBW低于2D脉动阵列的IBW，而SBW类似，IBW之差由张量B静止导致的时间重用引起

性能建模比较

PE利用率估计：\(\dfrac{\text{MACNum}}{\text{PENum}\times{\text{Latency}}}\)，延迟时间内PE进行的总MAC运算次数比上PE总数（假设每个PE每CC可进行一次MAC运算）

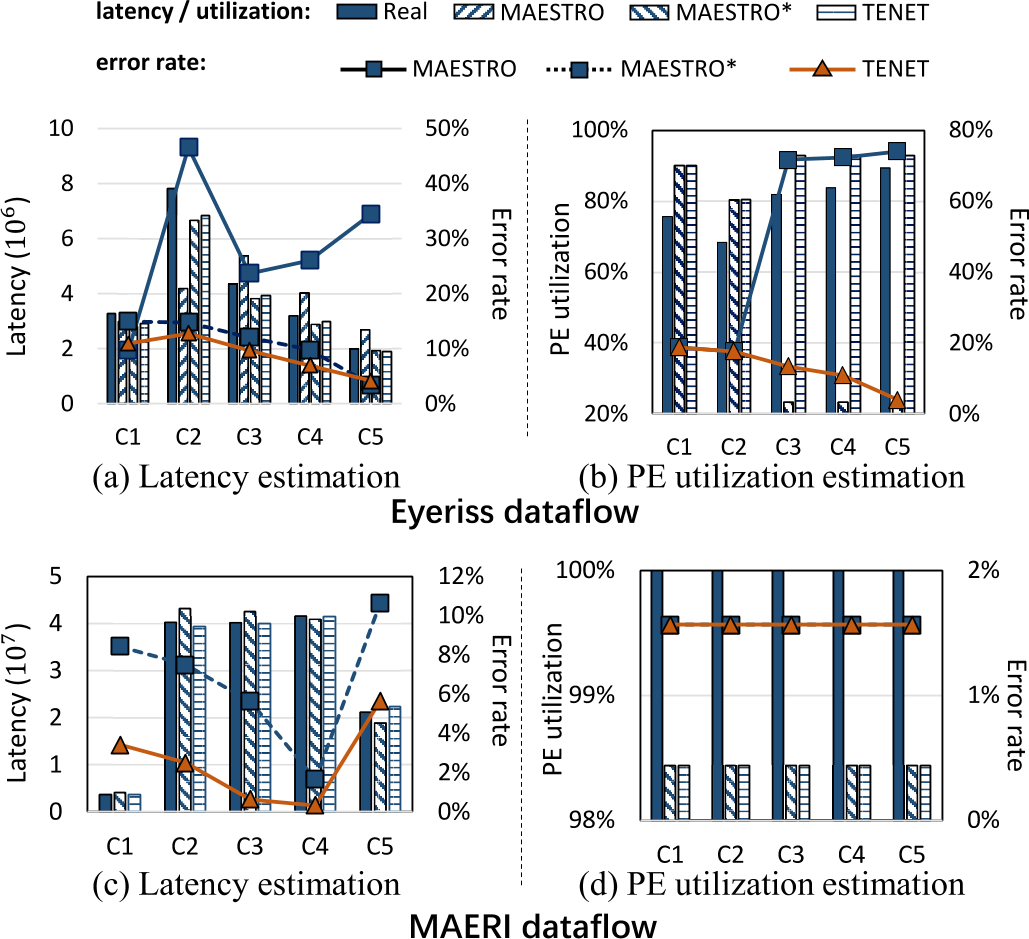
image.png

结论：TENET提高了性能估计准确率

  • TENET通过仿射变换，具有建模复杂数据流的能力
  • TENET通过遍历整个时空戳判断PE是否被分配，而不是使用简单的多项式进行PE利用率估计
  • MAESTRO缺陷：
    • MAESTRO需要所有数据维度被显式指定，故无法计算输出重用
    • MAESTRO只分析最内层的时空重用
    • MAESTRO不支持将多个数据维度映射到单个PE维度上