跳转至

Rubick： A Synthesis Framework for Spatial Architectures via Dataflow Decomposition

Info

Link: IEEE

摘要&结论

动机：基于符号的分析无法同时提供高效的硬件设计空间探索(DSE)与架构优化

  • 原因：符号和硬件底层细节存在语义鸿沟
    • 基于符号的分析无法捕获不同数据流间详细的架构特征

方法：将数据流分解为两个低级中间表示(IR)，即访问入口与数据布局，可提供空间架构的实现细节

  • 访问入口：数据如何从内存进入PE
  • 数据布局：数据如何排列、访存

优势：

  • 高效DSE
  • 生成优化后的硬件
    • 对于特定硬件平台可进行各种底层实现优化
  • 提供完整的数据流设计空间
    • 方法：分别形成2种IR的子空间

引言

高级记号存在的问题：空间架构包括PE和片上缓存，二者底层架构不同，无法从高级记号中推导出数据访存模式和数据排列方式

TENET缺陷：

  • 缺乏高效DSE方法
  • 由于TENET忽略了硬件实现细节，无法针对具体硬件限制（如扇入扇出）做数据流优化

贡献：

  • 提出访问入口、数据布局的IR以弥合数据流和硬件的差异
  • 根据新IR构建完整设计空间
    • 对每个IR构建设计子空间，通过在子空间消除非法和低效设计，整体降低整个设计空间大小，提升DSE效率
  • 展现端到端空间架构综合流程

背景

image.png

记号：

  • 迭代域和循环实例：\(D_S=\set{S(\vec n)\ |\ \vec n=(i,j,\cdots)}\)
  • 张量域：\(D_A=\set{A(\vec{n'})}\)
  • 访问函数：\(A_{D_S\to(D_A,D_B,\cdots)}=\set{S(\vec n)\to(A(\vec{n_A'}),B(\vec{n_B'}),\cdots)}\)
  • 空间数据流：\(\Theta_{D_S\to D_{st}}=\set{S(\vec n')\to(PE(\vec p)\ |\ T(\vec t))}\)
    • 数据流时空域：\(D_{st}\)
    • \(\vec t=(t_1,t_2,\cdots)\)：\(t_1\)为最内层循环
  • 张量移动：\(M_{D_{st}\to D_A}=\set{(PE(\vec p)\ |\ T(\vec t))\to A(\vec{n'})}\)

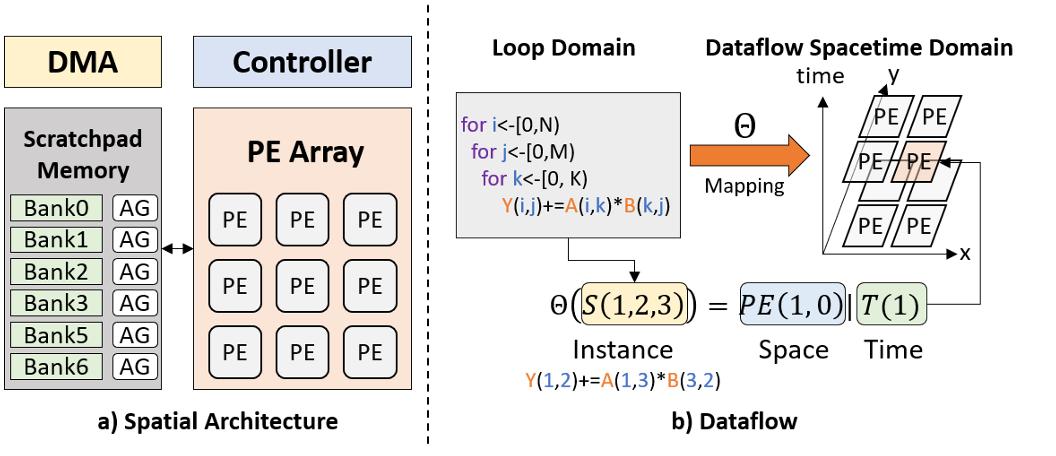
空间架构：

  • 假设：PE阵列为2D
  • 空间戳：\(PE(\vec p),\vec p=(x,y)\)
  • 时间戳：\(T(\vec t),\vec t=(t_1,t_2,\cdots)\)
  • 片上缓存：为了支持PE的并行访问，划分为库(bank)，通过地址生成器(AG)从库中选取数据

数据流分解

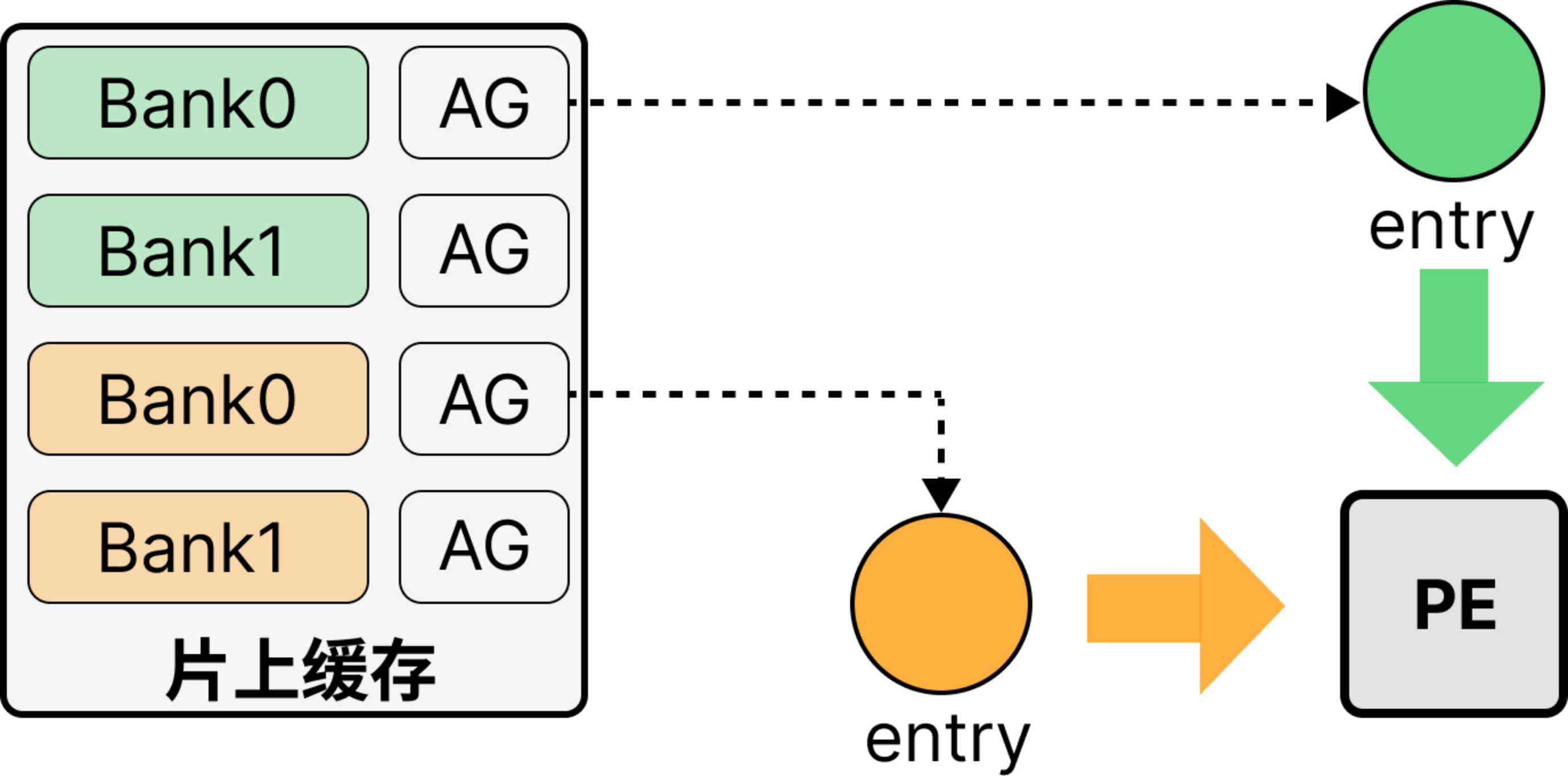
image.png

image.png

  • 核心思想：
    • 依据：空间架构 -> PE + 片上缓存
      • 二者通过入口(entry) 进行连接（片上缓存的数据通过entry输出，PE数据通过entry输入），利用entry作为二者自然分离点
    • 核心：数据流 -> 访问入口 + 数据布局
  • 概念：
    • 入口时空域\(E_{st}=\set{(E(\vec{p_e})\ |\ T(\vec{t_e}))}\)：入口时空戳构成的集合
      • 入口：负责从内存中加载数据，并发送至PE阵列
    • 访问入口：PE时空戳 -> 入口时空戳，即\(D_{st}\)使用的张量数据从哪一个入口在哪一个时间戳传出
      • 定义：\(\Omega_{D_{st}\to E_{st}}=\set{(PE(\vec{p_d})\ |\ T(\vec{t_d}))\to(E(\vec{p_e})\ |\ T(\vec{t_e}))}\)
      • 作用：
        • 指导片上缓存设计： \(\vec{p_e}\)决定内存库维度
        • 指导PE互联方式设计：通过\(\vec{t_e}\)识别数据移动方式，从而决定PE互联方式
      • 访问入口仅揭示入口到PE的数据访问及其访问方向，并不包含具体张量数据
    • 数据布局：入口时空戳 -> 张量数据，显示指定哪一个张量元素会被该入口传出（描述张量数据的空间排列及张量数据进出入口的顺序）
      • 定义：\(L_{E_{st}\to D_A}=\set{(E(\vec{p_e})\ |\ T(\vec{t_e}))\to A(\vec{n'})}\)
      • 作用：
        • 张量大小决定时间维度的边界，进而决定内存的大小
  • 数据流分解：
    1. 张量行为\(M_{D_{st}\to D_A}\)、计算实例\(D_S\)分离：\(\Theta_{D_{st}\to D_S}=(M_{D_{st}\to D_A}\otimes M_{D_{st}\to D_B}\otimes\cdots)\times A_{(D_A,D_B,\cdots)\to D_S}\)
      • 相当于对输入\((D_A,D_B,\cdots)\)做分解，使用\(\otimes\)连接
    2. 访问入口\(\Omega\)、数据布局\(L\)分离：\(M_{D_{st}\to D_A}=\Omega_{D_{st}\to E_{st}}^A\times L_{E_{st}\to D_A}\) + 综上，(2)代入(1)：\(\Theta_{D_{st}\to D_S}=((\Omega_{D_{st}\to E_{st}}^A\times L_{E_{st}\to D_A})\otimes(\Omega_{D_{st}\to E_{st}}^B\times L_{E_{st}\to D_B})\otimes\cdots)\times A_{(D_A,D_B,\cdots)\to D_S}\)

例：GEMM

image.png

  • 计算实例：\(Y(i,j)\text{+=}A(i,k)B(k,j)\)
  • 数据流：\(\Theta_{D_S\to D_{st}}=\set{S(i,j,k)\to(PE(k,j\%2)\ |\ T(i+j\%2,j/2))}\)
    • 其中\(0\leqslant i<2,0\leqslant k<2,0\leqslant j<4\)，空间架构为\(2\times2\)PE阵列，\(i\)为内层循环
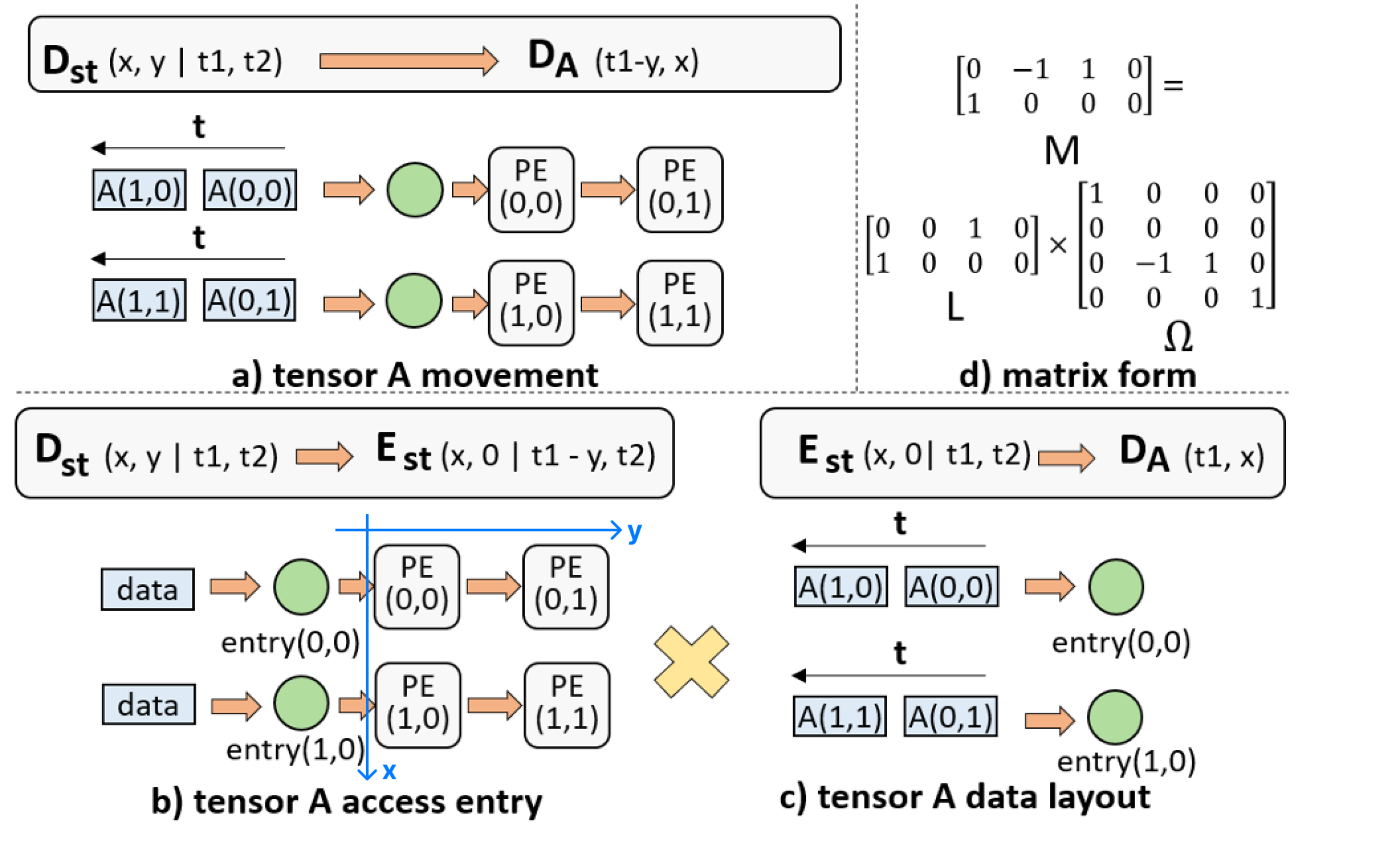
  • 张量移动：\(M_{D_{st}\to D_A}=\set{(PE(x,y)\ |\ T(t_1,t_2))\to A(t_1-y,x)}\)
    • 令\(k=x,j\%2=y,t_1=i+j\%2,t_2=j/2\)，则\(i=t_1-y,k=x\)
    • 记\((PE(x,y)\ |\ T(t_1,t_2))\)为\((x,y\ |\ t_1,t_2)\)
  • 访问入口：\(\Omega_{D_{st}\to E_{st}}^A=\set{(x,y\ |\ t_1,t_2)\to(x,0\ |\ t_1-y,t_2)}\)
  • 数据布局：\(L_{E_{st}\to D_A}=\set{(E(x,0)\ |\ T(t_1,t_2))\to A(t_1,x)}\)
    • 入口为1D，y恒等于0
    • 设定每行的数据按张量A的列顺序取用
  • 矩阵表示：\(M=L\Omega\)
    • \(\sigma_M(x,y,t_1,t_2)=\mathcal{L}(i,k),\sigma_L(x,y,t_1,t_2)=\mathcal{L}(i,k),\sigma_\Omega=T(\mathcal{L}(x,y,t_1,t_2))\)
    • \(M=\begin{bmatrix}&-1&1&\\1\end{bmatrix},L=\begin{bmatrix}&&1&\\1\end{bmatrix},\Omega=\begin{bmatrix}1&&&\\&&&&\\&-1&1&\\&&&1\end{bmatrix}\)
  • 推论：
    • 入口为1D，张量A仅有一个内存库
    • \((x,y\ |\ t_1,t_2),(x,y+1\ |\ t_1+1,t_2)\in D_{st}\to (x,0\ |\ t_1-y,t_2)\)，说明张量A在PE阵列水平移动，因此PE间需具备水平互联
    • \(A(t_1,x)\)在\((x,0)\)被访问，固定\(x\)（列号），说明每个内存库存储张量A的一列

数据流设计空间

核心：\(M_{D_{st}\to D_A}=\Omega_{D_{st}\to E_{st}}^A\times L_{E_{st}\to D_A}\)

  • 给定\(M\)，指定\(\Omega/L\)，求另一个
  • 分别指定\(\Omega,L\)，组合为\(M\)

子空间：

  • 访问入口空间\(\mathcal L(\Omega)\)：PE时空戳 -> 入口时空域所有线性变换的集合，由方向向量的线性组合决定
  • 数据布局空间\(\mathcal L(L)\)：时空戳 -> 张量域所有线性变换的集合

访问入口空间

假设：数据线性访问

  • 不存在非线性访问模式，如高次、分段
  • 意味着同一方向上数据行为一致

方向向量\(\vec r\)：

  • 概念：入口\((0,0)\)在0时刻的数据（时空戳\((0,0|0)\)）去到的PE时空戳
  • 定义：\(\Omega\vec r=\theta\)
    • \(\Omega^{-1}(0,0|0)\to\vec r\)
  • 性质：\(\vec r\)属于3D空间，共有7种基本方向向量
    • X脉动：\((1,0|1)\) Y脉动：\((0,1|1)\) 静止：\((0,0|1)\) X多播：\((1,0|0)\) Y多播：\((0,1|0)\) 对角脉动：\((1,1|1)\) 对角多播：\((1,1|0)\)
    • \(\vec r\not=0\)：此时未表达任何数据流动信息（\((0,0|0)\)去到\((0,0|0)\),平凡）
  • \(\Omega\)求解（\(\vec r\)确定\(\Omega\)）：
    1. 给定\(\vec r\)，为\(E(0,0|0)\)传播到的\(PE\)时空戳
    2. 约束：数据流在用一方向上行为一致，在\(x/y, t\)维度上再写两对映射，矩阵求逆 + 例：X脉动 \(\vec r=(1,0|1)\)
      • \(y+1\)，行为不变：\(PE(1,1|1)\to E(0,1|0)\)
      • \(t+1\)，行为不变：\(PE(1,0|2)\to E(0,0|1)\)
      • \(\Omega\begin{bmatrix}1&1&1\\0&1&0\\1&1&2\end{bmatrix}=\begin{bmatrix}0&0&0\\0&1&0\\0&0&1\end{bmatrix}\Rightarrow\Omega=\begin{bmatrix}0&0&0&\\0&1&0\\-1&0&1\end{bmatrix}\)
        • \(\Omega(x,y|t_1,t_2)=(0,y|t_1-x,t_2)\)
        • 不考虑高维时间\(t_2\)（张量大小大于架构大小时重现数据流）
  • \(\mathcal L(\Omega)\)求解：
    • \(\vec r\)为7种基本方向向量的线性组合，至少由其中1种构成，至多由其中3种构成（\(\vec r\)为3D），至多\(C_7^1+C_7^2+C_7^3=63\)种
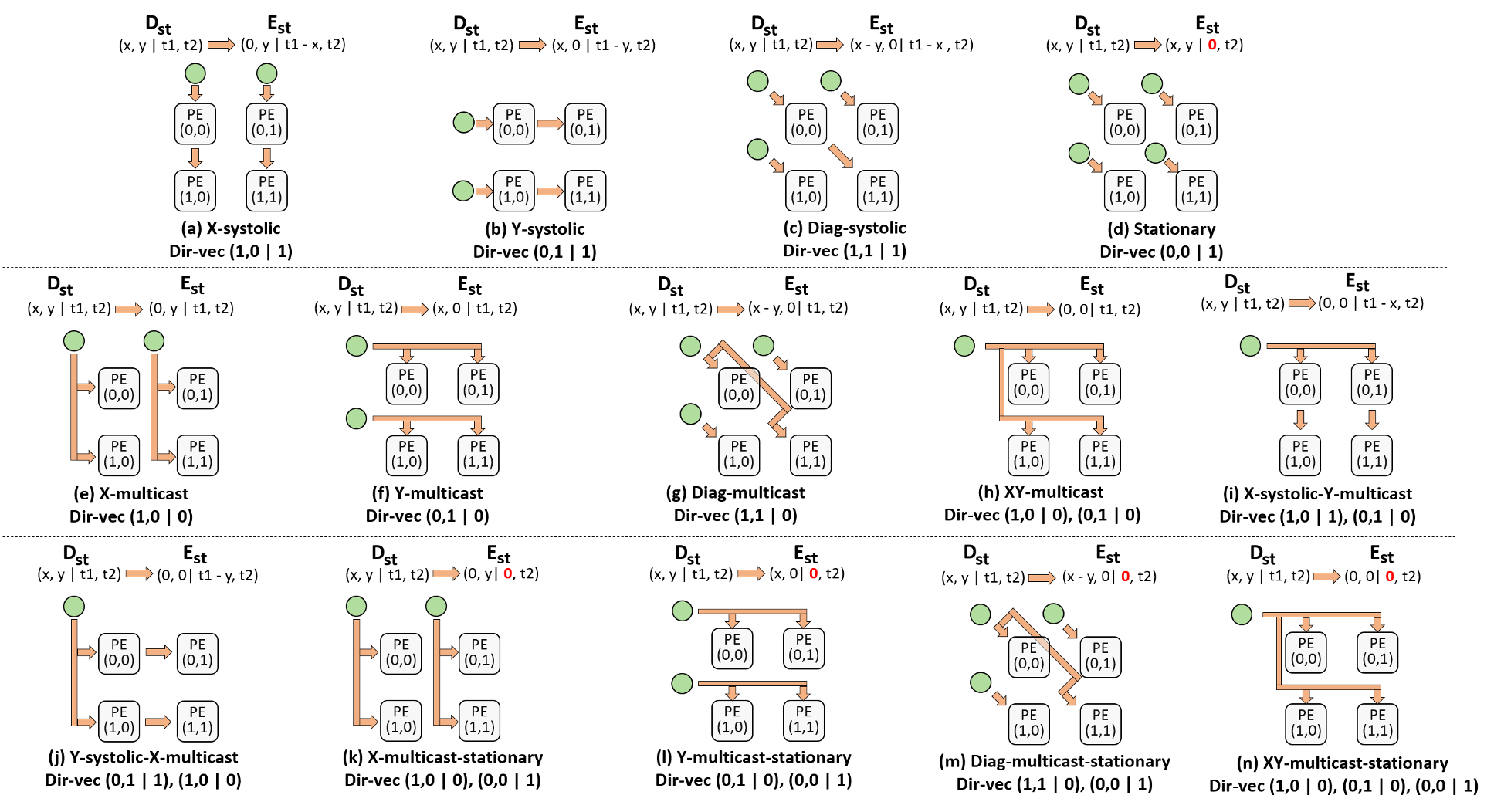
    • 去重、去对称，得到14种访问入口类型 image.png
  • 输出访问入口：将方向向量取反

数据布局空间

image.png

空间生成方法：线性矩阵变换

  • 变换对象：数据布局\(L\in\mathcal L(L),L(x,0\ |\ t)=(x,t)\)
    • 矩阵形式：\(L=\begin{bmatrix}1&&\\&&1\end{bmatrix}\)
  • 基本变换：
    1. 行交换：\(L'=\begin{bmatrix}&&1\\1&&\end{bmatrix}\)
      • 影响：\(L'(x,0\ |\ t)=(t,x),A(x,t)\to A(t,x)\)
      • 几何意义：张量A转置（图b）
    2. 行加：\(L'=\begin{bmatrix}1&&\\-1&&1\end{bmatrix}\)
      • 影响：\(L'(x,0|t)=(x,t-x),A(x,t)\to A(x,t-x)\)
      • 几何意义：张量A倾斜（图c）
    3. 行数乘：用于导致准放射变换（不常用）

综合流程

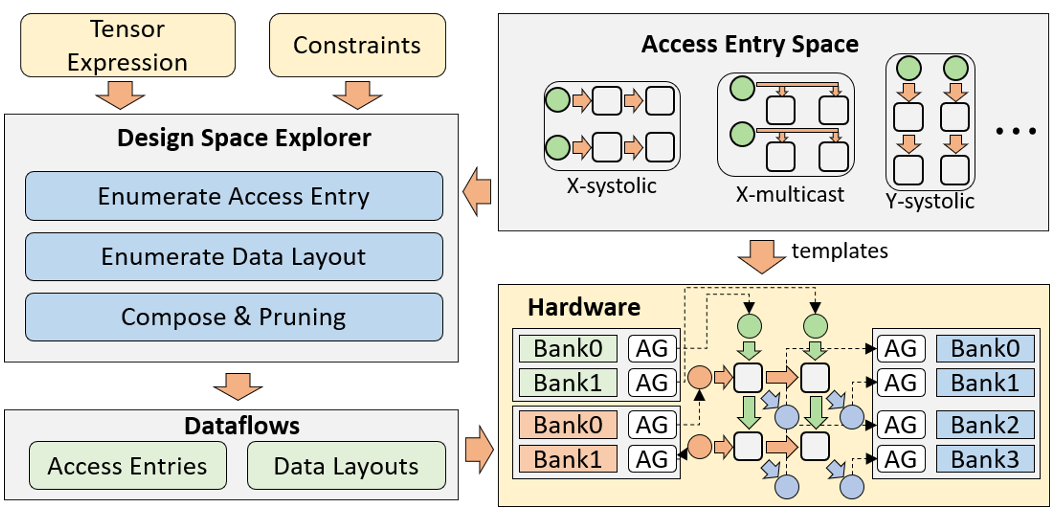
image.png

  • 目标：对于给定限制条件下的张量应用，生成最优硬件设计
  • 输入：
    • 张量表达式
    • 硬件限制：缓冲大小、资源等
    • 访问入口空间（可选）：限制硬件实现方式的子集
      • 如多播导致FPGA低频，可根据不同实现后端选择所需的设计子空间
  • DSE：分别枚举每个张量的访问入口和数据布局选择（PE阵列尺寸也可选择进行生成）
    • 根据数学约束剪枝（一一映射、时间非负等）
    • 理论复杂度关于循环层数、张量大小呈指数，通过数据流分解提前剪枝加速搜索
  • 输出：以两种IR的形式给出所有合法数据流
    • RTL（寄存器传输级）可由数据流针对特定后端生成
      • PE阵列由每个张量的访问入口决定
      • 片上缓存由内存库和AG构成，由数据布局决定

实验

方法：

  • 使用Chisel编译器生成Verilog RTL
  • 使用Vivado综合FPGA bitstream
  • 使用Synopsys进行ASIC实现，在UMC 55nm工艺下评估面积和功耗

延迟、扇入/扇出 trade off

方法：基于数据流不同张量的访问入口选择，实现延迟和扇入扇出的权衡

  • 访问入口(a)、(b)等采用脉动移动方式，内存口数量小（扇入扇出小，能耗小），但需要更多存取/输入输出周期（延迟高）
  • 访问入口(e)、(f)等采用多播方式，延迟低，但需更多线连接片上缓存，扇入扇出高

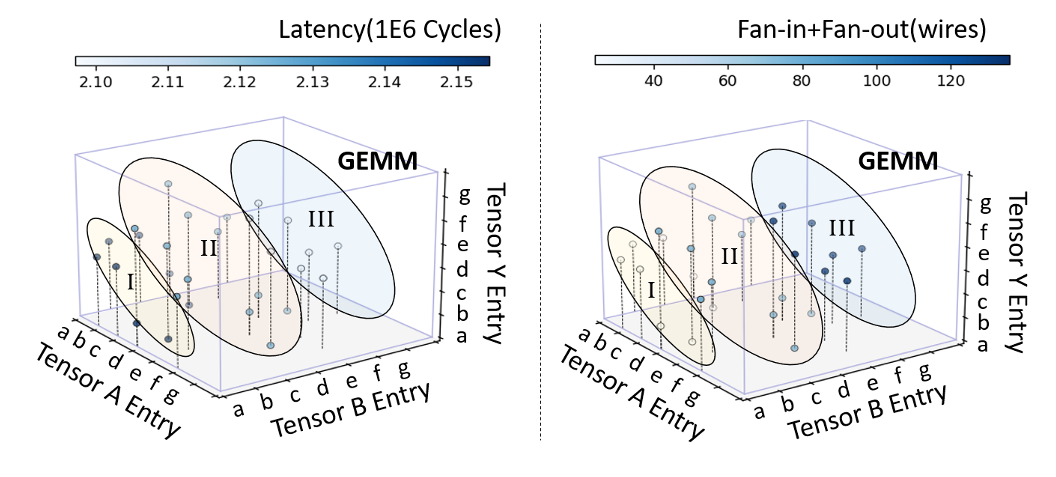
image.png

其中点坐标代表针对GEMM不同张量选择的访问入口组合（组合成数据流），颜色代表延迟与扇入扇出数

结论：Rubick 允许用户在线资源和延迟间进行权衡

  • 组I比组III减少了82.4%的线资源，仅增加了2.7%的延迟
  • 通过对扇入扇出进行刻画，可以在硬件约束下进行DSE

DSE 效率对比

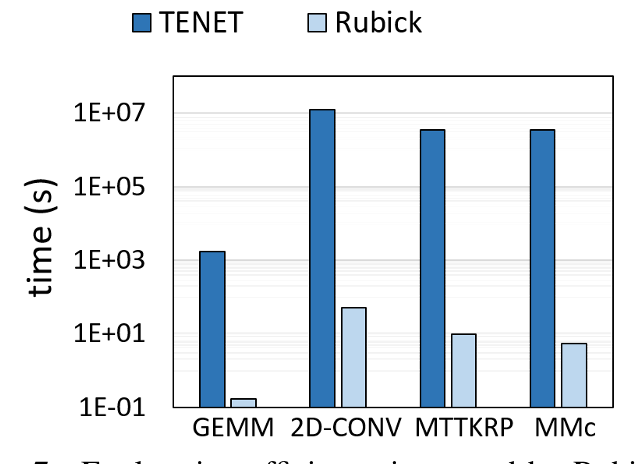
image.png

结论：

  • 设计空间的分解高效减少了总设计点数
  • 通过剪枝避免复杂度随循环层数增加而指数增长
  • PE阵列大小、计算精度与设计空间正交（无关）

FPGA 实现

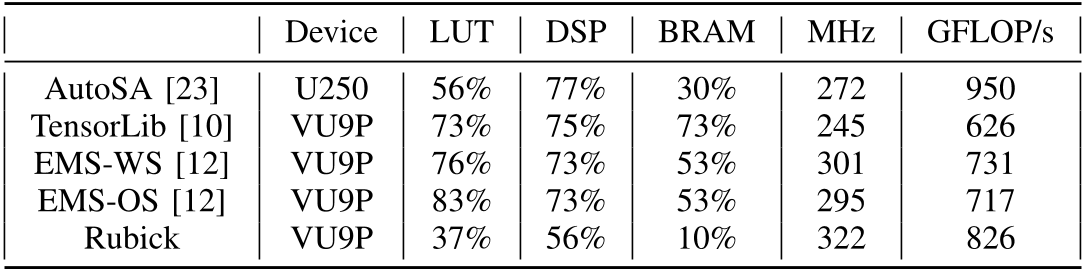
image.png

通过引入硬件限制条件提升性能：

  • 移除输入张量的多播方向向量（路由资源限制），频率提高7%
  • 输出张量采用X多播（配合加法器树），节省5倍BRAM
  • 通过简化控制逻辑进一步降低LUT和DSP

ASIC 面积、功率分析

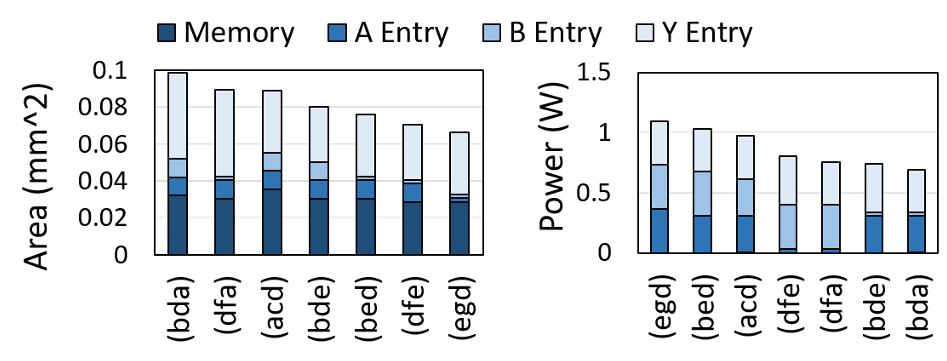
image.png

记号：(bda)表示GEMM中张量A, B, Y分别采用访问入口(a), (d), (b)

结论：

  • 输出张量访问入口占据绝大部分面积，因为需要实现约化操作（加法器树、累加器等）
  • 多播数据流面积更小，因为其通过线来广播数据
  • 内存功率可以忽略不计，因为PE阵列尺寸很小
  • 多播需要更多能耗，因为扇出大
  • 静止访问入口(d)最节约能耗，因为寄存器在大多数周期都空闲