A Quantum Algorithm for Shapley Value Estimation¶
Info
Link: arxiv
摘要&结论¶
目的：量子AI可解释性
对象：合作博弈中的Shapley值
内容：利用量子算法计算Shapley值
结论：将量子算法的Shapley值估计问题转化为估计二项分布真实平均值的多项式算法
导言¶
背景：AI可解释性：
- 使用可解释性模型
- 使用事后解释方法
Shapley值：对贡献进行度量
困难：直接计算Shapley值NP-Hard，仅能通过采样解决，无法精确计算
贡献：全局估计量子电路输入因素的Shapley值的框架
- 复杂度：\(O(n\log n)\)额外C-NOT门，\(O(n)\)额外电路深度，\(O(\log n)\)额外量子比特
- 对比：直接计算\(O(2^n)\)
背景¶
概念：
- 合作博弈：
- 博弈\(G=(F,V)\)
- 玩家\(F=\set{1,2,\cdots,N}\)
- 价值函数\(V\)，\(\forall S\subseteq F:V(S)\in\mathbb R\)，用于衡量给定合作\(S\)的价值，规定\(V(\emptyset)=0\).
- 收益向量\(\Phi(G)\)长度为\(N\)，\(\Phi(G)_i\)为玩家\(i\)的贡献（即Shapley值）；\(\Phi(G)\)由\(V\)决定，\(\Phi(G)_i\)由玩家\(i\)对\(V(S):\forall S\subseteq F\)的影响决定
- Shapley值：玩家\(i\)边缘贡献的期望
- 边缘贡献：\(\forall S\subseteq F\setminus\set{i}:V(S\cup\set{i})-V(S)\)
公理体系：\(G=(F,V),G'=(F,V'),F=\set{1,\cdots,N}\)，收益函数\(\Phi(G)\)
- 有效性：所有玩家贡献和等于所有玩家合作的价值$$ \sum_{i=1}^N\Phi(G)_i=V(F) $$
- 等价性：玩家\(i,j\)等价\(\Leftrightarrow \forall S\subseteq F,i,j\not\in S:V(S\cup\set{i})=V(S\cup\set{j})\),若玩家等价，则二者贡献相当$$ \Phi(G)_i=\Phi(G)_j $$
- 零玩家：玩家对任意合作都没有贡献\(\forall S\subseteq F,i\not\in S:V(S)=V(S\cup\set{i})\)，则为零玩家$$ \Phi(G)_i=0 $$
- 可加性：同一玩家在不同博弈中的Shapley值可加 $$ \Phi(G+G')=\Phi(G)_i+\Phi(G')_i $$ 其中\(G+G'=(F,V+V'),(V+V')(S)=V(S)+V'(S)\quad\forall S\subseteq F\) 该公里体系下，贡献划分唯一。
直接计算：记\(\Phi_i\equiv\Phi(G)_i\)，则$$ \Phi_i=\sum_{S\subseteq F\setminus\set{i}}\gamma(|F\setminus\set{i}|,|S|)\cdot(V(S\cup\set i)-V(S)) $$ $$ \gamma(n,m)=\dfrac{1}{(n+1)C_n^m}=\dfrac{m!(n-m)!}{(n+1)!} $$ 其中\(\dfrac{1}{C_n^m}=\dfrac{1}{C_{|F\setminus\set i|}^{|S|}}\)用于平均对于给定大小\(S\)的所有加和项，\(\dfrac{1}{n+1}=\dfrac{1}{N}\)用于平均不同大小的\(S\)的加和项。 困难：计算\(\Phi_i\)需要在\(2^{|F\setminus\set i|}\)个不同子集上计算\(V\)
可解释AI(XAI)：
- 黑箱程序无法调试，鲁棒性差，无法应对极端情况
- 事后分析的XAI可作为关键的调试工具
算法¶
思路：
- 将\(\gamma(n,m)\)转化为积分\(\int_0^1t^m(1-t)^{n-m}dt\)
- 对积分区间\([0,1]\)分割取点，计算Riemann和
记号：
- 价值函数上界\(V_\max:=\max\limits_{S\subseteq F}|V(S)|\)
- 子集编码\(S_x:=\set{j|x_j=1}\)，将子集编码为\(\ket x\)
- 约化价值\(\hat V^+(x):=\dfrac{V(S_x\cup\set i)}{V_\max},\hat V^-(x):=\dfrac{V(S_x)}{V_\max}\)
- 价值函数算子\(U_v^\pm\ket x\ket0:=\ket x\left(\sqrt{\dfrac{1-\hat V^\pm(x)}{2}}\ket0+\sqrt{\dfrac{1+\hat V^\pm(x)}{2}}\ket1\right)\)，\(U_v^\pm\)为\(U_v^+,U_v^-\)的缩写
- 类\(\beta\)函数\(B_{\alpha,\beta}=\int_0^1x^\beta(1-x)^{\alpha-\beta}dx\)，\(b_{\alpha,\beta}(x)=x^\beta(1-x)^{\alpha-\beta}\)
- 分点\(t_l(k)=\sin^2\left(\dfrac{\pi}{2}\cdot\dfrac{k}{2^l}\right)\)，\([0,1]\)上分割\(P=(t_l(k))_{k=0}^{2^l-1}\)，区间长度\(w_l(k)=t_l(k+1)-t_l(k)\)
- 汉明距离：两个二进制数之间不同的位的个数，\(H_m\)：到\(0\)汉明距离为\(m\)的二进制数的集合，即具有\(m\)个\(1\)的二进制数
步骤：
- 初态：\(\ket{\psi_0}=\ket0_{Pt}\otimes\ket0_{Pl}\otimes\ket0_{Ut}\)，分别为划分寄存器Pt，玩家寄存器Pl，贡献寄存器Ut
- 初始化划分寄存器：划分寄存器共\(l\)个qubit，\(l=O(\log n)\)将区间划分为\(2^l=n\)份；可以在\(O(n)\)的时间将其制备为任意态；将其初始化为\(\sum\limits_{k=0}^{2^l-1}\sqrt{w_l(k)}\ket k\)，得$$ \ket{\psi_1}=\sum_{k=0}^{2^l-1}\sqrt{w_l(k)}\ket k_{Pt}\ket0_{Pl}\ket0_{Ut} $$
- 取点带入：构造算子\(R\)，\(R\ket k\ket0:=\ket k(\sqrt{1-t_l'(k)}\ket0+\sqrt{t_l'(k)}\ket1)\)，其中\(t'_l(k)=t_{l+1}(2k+1)\)作为\([t_l(k),t_l(k+1)]\)的Riemann和采样点
证明：\(t_l(k)=\sin^2\left(\dfrac{\pi}{2}\cdot\dfrac{k}{2^l}\right)\)，\(t_{l+1}(2k+1)=\sin^2\left(\dfrac{\pi}{2}\cdot\dfrac{2k+1}{2^{l+1}}\right)=\sin^2\left(\dfrac{\pi}{2}\left(\dfrac{k}{2^l}+\dfrac{1}{2^{l+1}}\right)\right)\)
\(\therefore t_{l+1}(2k+1)\in[t_l(k),t_l(k+1)]\)
制备：
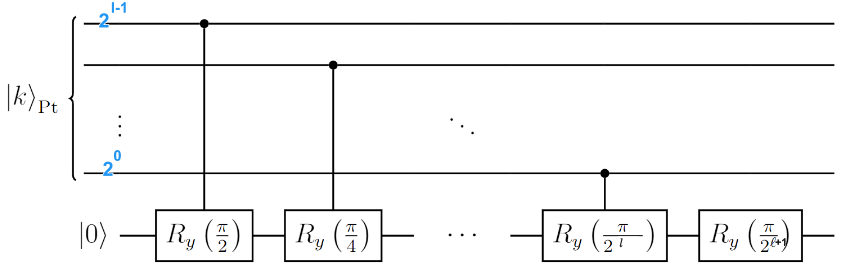\(R_y(\theta)\ket0=\cos\dfrac{\theta}{2}\ket0+\sin\dfrac{\theta}{2}\ket1\)
记\(k:=2^{l-1}a_{l-1}+\cdots+2^0a_0\)，则\(\dfrac{k}{2^l}=\dfrac{1}{2^1}a_{l-1}+\cdots+\dfrac{1}{2^l}\)
\(\begin{array}{l}\therefore Ry\left(\dfrac{k}{2^l}\pi+\dfrac{\pi}{2^{l+1}}\right)\ket0=\cos\left(\dfrac{k\pi}{2^l\cdot2}+\dfrac{\pi}{2^{l+1}\cdot2}\right)\ket0+\sin\left(\dfrac{k\pi}{2^l\cdot2}+\dfrac{\pi}{2^{l+1}\cdot2}\right)\ket1\\=\sqrt{1-t_l'(k)}\ket0+\sqrt{t_l'(k)}\ket1\end{array}\)
门复杂度\(O(\log n)\) - 构造幂次：对玩家寄存器中的每个比特作用算子\(R\)，得 $$ \ket{\psi_2}=\sum_{k=1}^{2^l-1}\sqrt{w_l(k)}\ket k_{Pt}\left(\sqrt{1-t_l'(k)}\ket0+\sqrt{t_l'(k)}\ket1\right)^{\otimes n}\ket0_{Ut} $$ 复杂度\(O(n\log n)\). 按照汉明距离划分量子态，化简张量积：事实上，玩家寄存器基中含\(1\)个数相同的量子态，其系数相同，相当于计算张量积中\(\sqrt{t_l'(k)}\ket1\)的贡献
其中\(\sum\limits_{m=0}^n\)枚举玩家寄存器中含有\(1\)的个数，且对于给定的\(m\)，基\(\ket h,h\in H_m\)具有相同的系数. 交换求和次序有 $$ \ket{\psi_2}=\sum_{m=0}^n\sum_{h\in H_m}\sum_{k=0}^{2^l-1}\sqrt{w_l(k)t_l'(k)^m(1-t_l'(k))^{n-m}}\ket k_{Pt}\ket h_{Pl}\ket0_{Ut} $$ 5. 查询价值：记\(U_V^\pm\ket h\ket0:=\ket h\ket{V^\pm(h)}\)，其中\(\ket{V^\pm(h)}=\sqrt{\dfrac{1-\hat V^\pm(h)}{2}}\ket0+\sqrt{\dfrac{1+\hat V^\pm(h)}{2}}\ket1\) 算子\(U_V^\pm\)实现思路：查找表，qRAM 作用\(U_V^\pm\ket h_{Pl}\ket0_{Ut}=\ket h_{Pl}\ket{V^\pm(h)}_{Ut}\)，得
至此，目标量子态已制备完毕.
- 结果读出：利用密度算子分离子系统，密度算子\(\ket{\psi_3^\pm}\bra{\psi_3^\pm}\)对划分寄存器、玩家寄存器取偏迹，得
偏迹：张量积的逆运算，用于分离子系统
给定\(\rho^{AB}=\rho^A\otimes\rho^B\)，已知\(\rho^A\)，则\(\rho^B=\text{tr}_A(\rho^{AB})\)
其中\(\text{tr}_A(\rho^{AB})=\sum\limits_{i=0}^{n-1}(\bra i\otimes I_n)\rho^{AB}(\ket i\otimes I_n)\)，相当于对其中的\(\rho^A\)成分取迹
对双比特系统而言，\(\text{tr}_B(\ket{a_1}\bra{a_1}\otimes\ket{b_1}\bra{b_2})\equiv\ket{a_1}\bra{a_2}\text{tr}(\ket{b_1}\bra{b_2})=\braket{b_2|b_1}\ket{a_1}\bra{a_2}\)
其中\(B_{n,m}=\gamma(n,m)\)可由分部积分 + 数归证明
结合\(\ket{V^\pm(h)}=\sqrt{\dfrac{1-\hat V^\pm(h)}{2}}\ket0+\sqrt{\dfrac{1+\hat V^\pm(h)}{2}}\ket1\) 故测量\(Ut\)寄存器的期望\(E=0\cdot P(\ket0)+1\cdot P(\ket1)=P(\ket1)\)为
- 后处理：执行上述过程两次，分别使用\(\hat V^+\)和\(\hat V^-\)算子，两次期望值相减得 $$ \dfrac{1}{2}\sum_{m=0}^n\sum_{h\in H_m}\gamma(n,m)\left(\hat V^+(h)-\hat V^-(h)\right) $$ 其中\(\sum\limits_{m=0}^h\sum\limits_{h\in H_m}\)相当于按照子集大小枚举全部子集，带入得 $$ \dfrac{1}{2\cdot V_\max}\sum_{S\subseteq F\setminus\set i}\gamma(|F\setminus\set i|,|S|)(V(S\cup\set i)-V(S))=\dfrac{\Phi_i}{2\cdot V_\max} $$
综上，总的量子电路为：
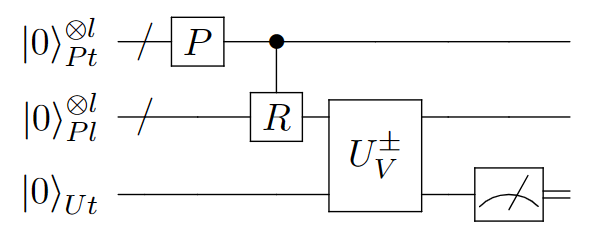
其中\(P\)用于制备分割，\(R\)用于带入每个分割区间的取点，\(U_V^\pm\)用于价值函数的计算；测量时，划分寄存器随收益寄存器的塌缩完成了积分即\(\gamma\)函数的计算，玩家寄存器随塌缩完成了子集的枚举，而收益寄存器则塌缩为求和对象，通过求期望得到了所需的结果
误差分析：定义分割加细时左区间占原区间比例\(\rho_{l-1}(k):=\dfrac{w_l(2k)}{w_l(2k)+w_l(2k+1)}=\dfrac{w_l(2k)}{w_{l-1}(k)}\)
结合对称性、单调性知\(\rho_l(k)\in\left(\dfrac{1}{4},\dfrac{3}{4}\right)\)
利用Darboux上下和估计误差上界，可证随分割加细，单调区间误差上界\(\overline{\text{SUE}_{n,m}}(l+1)\leqslant\dfrac{3}{4}\overline{\text{SUE}_{n,m}}(l)\)，即每次分割误差至少缩减至原误差的\(75\%\).