基于量子计算的投资组合优化算法

Info

该工作为朱学长@11d-beyonder的毕业设计

本文为该工作的阅读笔记

概括总结

1. 将投资组合问题表达为二次优化模型
2. 利用拉格朗日乘子法将二次优化问题转化为方程组求解问题
3. 利用HHL算法求解方程组
4. 通过引入约束缩放系数对算法进行优化

具体内容

标准投资组合选择模型

$$ \begin{array}{rl} \text{minimize}&w^{\mathrm T}\Sigma w\ s.t.&w^{\mathrm T}R=E\ &w^{\mathrm T}\Pi=\Xi \end{array} $$ 其中

• \(w=[w_1,\cdots,w_n]^\mathrm T,\sum w_i=1\)为选择在\(n\)个标的上投资的比例
• \(r_t=[r_1^t,\cdots,r_n^t]^\mathrm T\)为每个标的在交易日\(t\)的收益
• \(R=\mathbb E(r_t)=\dfrac{1}{T}\sum r_t\)为\(T\)个交易日收益的均值
• \(\Sigma=\mathbb V(r_t)=\dfrac{1}{T-1}\sum(r_t-R)^\mathrm T(r_t-R)\)为收益的协方差矩阵
• \(E=w^\mathrm TR\)为期望收益
• \(V=w^\mathrm T\Sigma w\)为风险
• \(\Pi\)为当前的价格向量
• \(\Xi\)为投资金额限定

  取\(\Pi=[1,\cdots,1]^\mathrm T\)时\(w\)为各标的投资的份数，\(\Xi\)为购买份数限额

故上式表示期望一定时，选取风险最低的投资组合。

拉格朗日乘子法

\[ f(w)=w^\mathrm T\Sigma w+\eta(w^\mathrm TR-E)+\rho(w^\mathrm T\Pi-\Xi) \]

其中\(\eta,\rho\)为拉格朗日乘子。求偏导，得

\[ \left\{ \begin{array}{l} \dfrac{\partial f}{\partial w}=2\Sigma w+\eta R+\rho \Pi=0\\ \dfrac{\partial f}{\partial\eta}=w^\mathrm TR-E=0\\ \dfrac{\partial f}{\partial\rho}=w^\mathrm T\Pi-\Xi=0 \end{array} \right. \]

即

\[ \begin{bmatrix} 0&0&R^\mathrm T\\ 0&0&\Pi^\mathrm T\\ R&\Pi&\Sigma \end{bmatrix} \begin{bmatrix} \eta\\ \rho\\ w \end{bmatrix}= \begin{bmatrix} E\\ \Xi\\ 0 \end{bmatrix} \]

此处对系数进行了调整

记该方程组为\(Ax=b\)，利用HHL求解（由于协方差矩阵\(\Sigma\)实对称，故\(A\)自伴）

\[ \begin{bmatrix} A&O\\ O&I \end{bmatrix} \begin{bmatrix} x\\ 0 \end{bmatrix}= \begin{bmatrix} b\\ 0 \end{bmatrix} \]

---

优化：引入约束缩放系数降低矩阵的条件数

\[ \begin{bmatrix} 0&0&s_1R^\mathrm T\\ 0&0&s_2\Pi^\mathrm T\\ s_1R&s_2\Pi&\Sigma \end{bmatrix} \begin{bmatrix} \eta\\ \rho\\ w \end{bmatrix}= \begin{bmatrix} E\\ \Xi\\ 0 \end{bmatrix} \]

HHL

概述

求解\(Ax=b\)，其中\(A\)自伴（\(A\)不自伴：构造\(\begin{bmatrix}&A\\A^\dagger\end{bmatrix}\begin{bmatrix}0\\x\end{bmatrix}=\begin{bmatrix}b\\0\end{bmatrix}\)）

复杂度：\(O(\kappa^2\epsilon^{-1}\log N)\)，其中\(\kappa\)为矩阵的条件数，\(\epsilon\)为解的精度（相位估计求特征值时，特征值倒数的相对误差）

表示

\(A\ket x=\ket b\Rightarrow\ket x=A^{-1}\ket b\)

谱分解：\(A=\sum\limits_{j=0}^{N-1}\lambda_j\ket{\mu_j}\bra{\mu_j}\)

标正基：\(\ket b=\sum\limits_{j=0}^{N-1}\beta_j\ket{\mu_j}\)

代入：

\[ \begin{array}{rlr} \ket x&=\left(\sum\limits_{i=0}^{N-1}\dfrac{1}{\lambda_i}\ket{\mu_i}\bra{\mu_i}\right)\left(\sum\limits_{j=0}^{N-1}\beta_j\ket{\mu_j}\right)&(\text{对角阵})\\ &=\sum\limits_{j=0}^{N-1}\dfrac{1}{\lambda_j}\beta_j\ket{\mu_j}&(\text{标正基}) \end{array} \]

电路

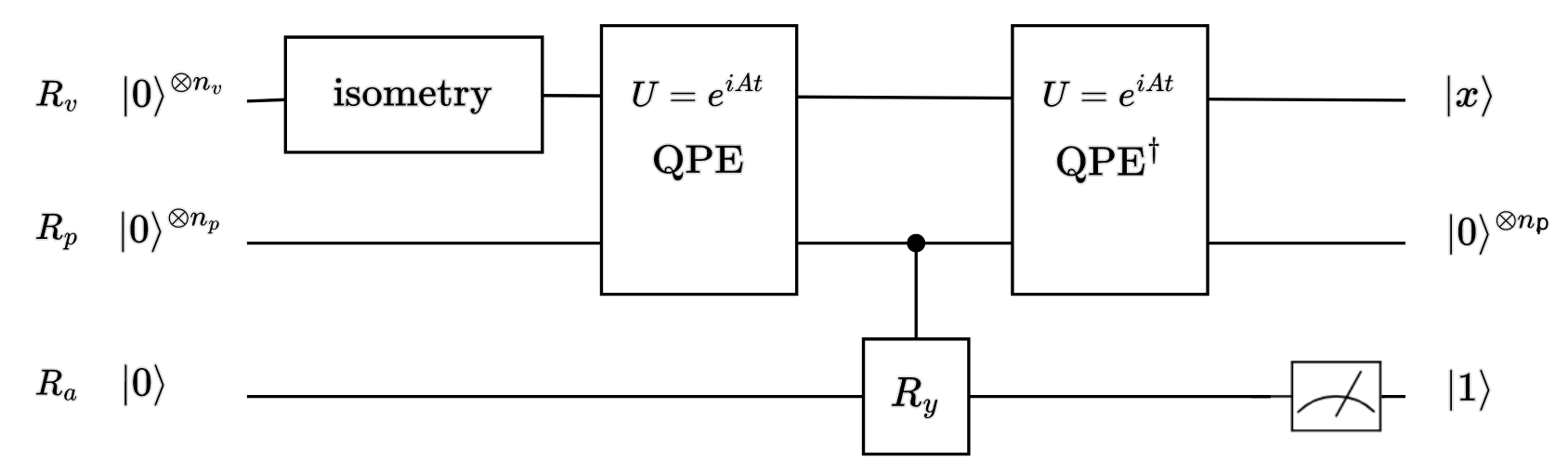
1. 利用同构电路将\(\ket b=\sum\limits_{j=0}^{N-1}b_j\ket j=\sum\limits_{j=0}^{N-1}\beta_j\ket{\mu_j}\)置于\(R_v\)上（需提前将\(\ket b\)归一化）
2. 经过QPE，得\(\sum\limits_{j=0}^{N-1}\beta_j\ket{\mu_j}\ket{\varphi_j}\)
3. 对于取定的归一化常数\(C\)，对\(R_a\)作用\(R_Y(\theta)\)，得\(\sum\limits_{j=0}^{N-1}\beta_j\ket{\varphi_j}\ket{\mu_j}\left(\cos\dfrac{\theta}{2}\ket0+\sin\dfrac{\theta}{2}\ket1\right)\)，其中
   • \(\theta=2\arcsin\dfrac{C}{\lambda_j}\)（由目标方程解的形式决定，\(C\)用于归一化与成功率控制）
   • \(\lambda_j\)由\(\varphi_j\)决定
   • \(R_p\)存储\(\varphi_j\) 带入\(C\)，得\(\sum\limits_{j=0}^{N-1}\beta_j\ket{\mu_j}\ket{\varphi_j}\left(\sqrt{1-\dfrac{C^2}{\lambda_j^2}}\ket0+\dfrac{C}{\lambda_j}\ket1\right)\)
4. 利用QPE\(^\dagger\)解纠缠，得\(\sum\limits_{j=0}^{N-1}\beta_j\ket{\mu_j}\ket0^{\otimes n}\left(\sqrt{1-\dfrac{C^2}{\lambda_j^2}}\ket0+\dfrac{C}{\lambda_j}\ket1\right)\)
5. 测量辅助比特，测量结果为1时成功求解，得目标态\(\dfrac{1}{\sqrt{\sum\limits_{j=0}^{N-1}\dfrac{\beta_j^2}{\lambda_j^2}}}\sum\limits_{j=0}^{N-1}\dfrac{\beta_j}{\lambda_j}\ket{\mu_j}\ket0^{\otimes n}\ket1\)，其中\(\dfrac{1}{\sqrt{\sum\limits_{j=0}^{N-1}\dfrac{\beta_j^2}{\lambda_j^2}}}\sum\limits_{j=0}^{N-1}\dfrac{\beta_j}{\lambda_j}\ket{\mu_j}\)为标准化的\(\ket x\)
6. 利用量子振幅估计得到基上的系数

细节

参数确定

A

创新：使用A的特征值进行缩放

要求：\(|\lambda|\leqslant1\)

缩放：\(A:=\dfrac{l}{|\lambda|_\max}A(l\in(0,1])\)

取\(l=\dfrac{1}{2}\)，此时

• \(|\lambda|_\min\leqslant|\lambda|\leqslant|\lambda|_\max\)，自伴：\(A=A^\dagger\Rightarrow\kappa=\dfrac{\max\sigma(\sqrt{AA^\dagger})}{\min\sigma(\sqrt{AA^\dagger})}=\dfrac{|\lambda|_\max}{|\lambda|_\min}\)
• \(\dfrac{|\lambda|_\min}{2|\lambda|_\max}\leqslant\dfrac{|\lambda|}{2|\lambda|_\max}\leqslant\dfrac{|\lambda|_\max}{2|\lambda|_\max}\Rightarrow|\lambda'|\in[\dfrac{1}{2\kappa},\dfrac{1}{2}]\)

U

利用哈密顿模拟得\(U=e^{iAt}\)，其中\(t\)为模拟时间

对角阵：\(iAt=\sum\limits_{j=0}^{N-1}i\lambda_jt\ket{\mu_j}\bra{\mu_j}\Rightarrow U=\sum\limits_{j=0}^{N-1}e^{i\lambda_jt}\ket{\mu_j}\bra{\mu_j}\)

标正基：\(U\ket{\mu_j}=e^{i\lambda_jt}\ket{\mu_j}\)

\(\lambda\)

QPE求得的\(\varphi\)满足\(U\ket\mu=e^{2\pi i\varphi}\ket\mu(\varphi\in[0,1))\)

又\(U\ket\mu=e^{i\lambda t}\ket\mu\)，故\(e^{2\pi i\varphi}=e^{i\lambda t}\)

\(\lambda\geqslant0\)时，\(\varphi=\dfrac{\lambda t}{2\pi}\)

\(\lambda<0\)时，\(e^{2\pi i}=1\Rightarrow e^{i\lambda t}=e^{2\pi i\frac{\lambda t}{2\pi}}=e^{2\pi i(\frac{\lambda t}{2\pi}+1)}=e^{2\pi i\varphi}\Rightarrow\varphi=1+\dfrac{\lambda t}{2\pi}\)

取\(t=\pi\)，有\(\varphi=\left\{\begin{array}{ll}\dfrac{\lambda}{2},&\lambda\geqslant0,\\1+\dfrac{\lambda}{2},&\lambda<0.\end{array}\right.\)

又\(|\lambda|<1\)，故\(\lambda=\left\{\begin{array}{ll}2\varphi,&\varphi<\dfrac{1}{2},\\2(\varphi-1),&\varphi\geqslant\dfrac{1}{2}.\end{array}\right.\)

\(n_p\)

用\(n_p\)个比特近似\(\varphi\)时绝对误差\(|\varphi-\tilde\varphi|<2^{-n_p}\)

故\(|\lambda-\tilde\lambda|<2^{1-n_p}\)

由\(\epsilon\)定义（特征值倒数的相对误差）与\(|\lambda|\)下界\(\dfrac{1}{2\kappa}\)得

\[ \left|\dfrac{\dfrac{1}{\lambda}-\dfrac{1}{\tilde\lambda}}{\dfrac{1}{\lambda}}\right|\approx\left|\dfrac{\tilde\lambda-\lambda}{\lambda}\right|\leqslant\dfrac{\kappa}{2^{n_p-2}}\leqslant\epsilon\Rightarrow n_p\geqslant2+\log_2\dfrac{\kappa}{\epsilon} \]

C

算法成功率\(P(\ket1)=\sum\limits_j\dfrac{C^2\beta_j^2}{\lambda_j^2}\)

约束：\(\left|\dfrac{C}{\lambda_j}\right|\leqslant1\Rightarrow |C|\leqslant|\lambda|_\min\)

为提高成功率，取\(|C|=|\lambda|_\min\)

结果处理

为求得\(\ket x\)，需求出\(\ket x\)的范数\(\sqrt{\sum\limits_{j=0}^{N-1}\dfrac{\beta_j^2}{\lambda_j^2}}\)

又\(P(\ket1)=\sum\limits_{j=0}^{N-1}\dfrac{C^2\beta_j^2}{\lambda_j^2}\)

故\(||x||=\dfrac{\sqrt{P(\ket1)}}{C}\)

基础知识

协方差矩阵

协方差：用于刻画两个随机变量的相似程度

\[ \sigma(x,y)=\dfrac{1}{n-1}\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y) \]

设有随机变量\(\set{x_1,\cdots,x_n}\)，两两之间的协方差为\(\sigma(x_m,x_k)=\dfrac{1}{n-1}\sum\limits_{i=1}^n(x_{mi}-\bar{x_m})(x_{ki}-\bar{x_k})\) 则协方差矩阵为

\[ \Sigma=\begin{bmatrix} \sigma(x_1,x_1)&\cdots&\sigma(x_1,x_n)\\ \vdots&&\vdots\\ \sigma(x_n,x_1)&\cdots&\sigma(x_n,x_n) \end{bmatrix} \]

为实对称阵

向量&二次型求导

向量对向量求导

分母的每个元素对整个分子求导，求导后的结果按照分母的形状进行组装

二次型求导

\[\begin{array}{l}d(x^\mathrm TAx)=(x^\mathrm TA)dx+d(x^\mathrm TA)x=x^\mathrm TAdx+(d(x^\mathrm TA)x)^\mathrm T\\=x^\mathrm TAdx+x^\mathrm Td(A^\mathrm Tx)=x^\mathrm TAdx+x^\mathrm TA^\mathrm Tdx=x^\mathrm T(A+A^\mathrm T)dx\end{array}\]

\(A\)实对称\(\Rightarrow\dfrac{d(x^\mathrm TAx)}{dx}=2Ax\)

矩阵的条件数

矩阵范数：矩阵对向量的缩放能力

\[ ||A||=\max_x\dfrac{||Ax||}{||x||} \]

由定义知，\(||A^{-1}||=\max\limits_y\dfrac{||A^{-1}y||}{||y||}=\dfrac{1}{\min\limits_y\dfrac{||y||}{||A^{-1}y||}}\overset{y=Ax}{=}\dfrac{1}{\min\limits_x\dfrac{||Ax||}{||x||}}\)

条件数：衡量方程的稳定性

\[ \kappa(A)=||A||||A^{-1}|| \]

易证，当\(x\)变化\(\delta x\)时，有\(\dfrac{1}{\kappa(A)}\dfrac{||\delta b||}{||b||}\leqslant\dfrac{||\delta x||}{||x||}\leqslant\kappa(A)\dfrac{||\delta b||}{||b||}\)

计算：\(||A||\)为A最大奇异值\(\max\sigma(\sqrt{AA^\dagger})\)，\(||A^{-1}||\)为A最小奇异值的倒数\(\dfrac{1}{\min\sigma(\sqrt{AA^\dagger})}\)

QPE

设\(U\)的特征向量\(\ket\mu\)的特征值为\(e^{2\pi i\varphi}\)，即\(U\ket\mu=e^{2\pi i\varphi}\ket\mu\)，电路黑盒如下

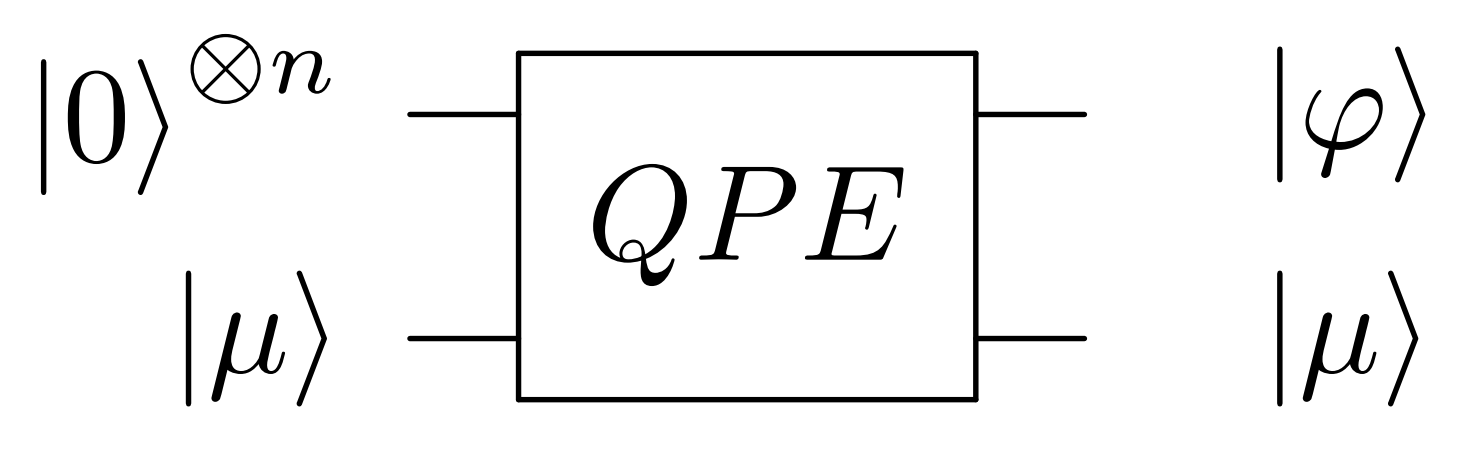
当\(\ket v=\sum v_j\ket{\mu_j}\)时，结果为\(\sum v_j\ket{\varphi_j}\)