程序抽象表示基础
编译:对程序表示和架构细节不断抽象
- 使用数学模型求解、计算
抽象表示在编译器中发挥的作用¶
多面体模型:对满足一定约束的循环嵌套进行分析和优化的数学抽象模型
- 基于程序语句实例:一条语句每次执行对应不同实例,一个数组元素每次访问对应不同的内存单元访问
- 使用表示的组合进行抽象:集合 + 映射
多面体模型 VS 幺模变换
多面体适用范围更广:
- 多面体不受限于矩阵行列式绝对值为1
- 幺模变换局限于循环变换、循环倾斜和循环反转的组合
多面体模型数学建模实例
代码:其中N为编译时未知的符号常量
约束集合:将约束转化为\(\geqslant0\)的形式(假设所有变量满足整数约束,即\(i>n\Leftrightarrow i\geqslant n+1\))
\(\set{i\geqslant3,i<10,j\geqslant i,j<N}\Rightarrow\set{i-3\geqslant0,-i+9\geqslant0,j-i\geqslant0,-j+N-1\geqslant0}\)
矩阵形式:
近似仿射约束表达:\((i+1)\%2=0\)
\(\exists e:i+1=2e\Leftrightarrow\exists e:(i+1)-2e\geqslant0\land-(i+1)+2e\geqslant0\)
访存关系:读/写访存关系的集合
\(\set{S_1(i,j)\to A(j,i):3\leqslant i<9\land i\leqslant j<N\land(i+1)\%2=0}\)
执行顺序式:从左到右,从上到下
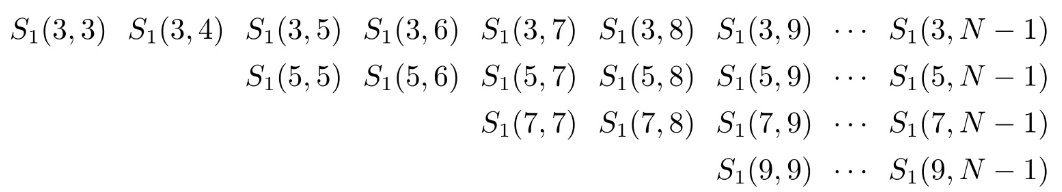
访问顺序式:

优化:当数组A在内存中按行优先存储,则数组访问顺序无局部性;使用循环交换
- 优化依据:语句实例和数组存储的内存地址单元之间的关系
优化结果:精确计算交换后的循环边界,处理编译阶段未知的符号常量(加入min/max操作)
多面体模型中的抽象¶
多面体通过构建优化模型实现对程序的变换
- 变换的基础是程序的表示
整数集合与仿射函数¶
多面体模型程序表示(中间表示)的数学基础:整数集合,仿射函数
- 多面体模型要求待分析的变换的循环嵌套满足静态仿射约束
- 静态仿射约束(Static Control Parts, SCoP):满足下列条件的程序语句的最大集合
- 包裹这些程序语句的循环的边界、步长和控制流语句的条件只能是外层循环索引变量和符号常量的仿射函数
- 多面体模型无法处理
A[i×j]等下标表示,break,continue等运行时确定的控制流信息 - 故多面体模型关注仿射函数
- 静态仿射约束(Static Control Parts, SCoP):满足下列条件的程序语句的最大集合
整数集合¶
命名整数空间:语句标识符\(S_i\) + 整数\(d\)元组(未命名整数空间)
命名整数集合:带有循环边界和循环步长约束的命名整数空间
- 约束使用Presburger公式表示,Presburger公式是Presburger语言的一阶谓词公式
- 比较:字典序
一阶逻辑形式系统
语言:一组符号的集合
- 组成:变元、常数、函数、谓词、逻辑符号
函数符号:对象之间的某种操作或映射(与函数类似)
常数符号:表示某个特定的对象或元素
谓词符号:表示对象之间的关系或属性,接受若干个对象作输入,返回一个真值,表示对象是否满足某种关系
变量:表示不同值的对象或元素
- 自由变量:不被量词绑定的变量
- 约束变量:被量词限定的变量
公式符号:用于构建逻辑公式的符号
- 组成:逻辑运算符、量词、常数符号、变量、函数符号、谓词符号
Presburger语言
Presburger语言:以下列符号为公式符号的一阶谓词语言(/0, /2表示接受参数个数),多面体模型对Presburger语言的变量限定范围为\(\mathbb Z\)
- 函数符号 + /2 => 两个整数的加法
- 函数符号 - /2 => 两个整数的减法
- 一个针对整d的常数符号 d /0 => 对应的整数值
- 一个针对正整数d的单目函数符号 \(\lfloor\cdot/d\rfloor\) => 对d进行整型除法
- 一组常数符号 \(c_i\) /0
- 谓词符号 \(\leqslant\) /2 => 两个整数的小于等于关系
Presburger语言的项:由下列表述递归定义
- Presburger语言的一个变量v
- \(f_i(t_1,\cdots,t_{r_i})\),其中\(f_i\)为Presburger语言的一个函数符号,\(t_i(1\leqslant j\leqslant r_i)\)为Presburger语言的项
- \(r_i=0\), \(f_i()\)也是Presburger语言的项,用于表示标量
Presburger公式:由下列表示递归定义的一阶谓词公式
- 布尔值true
- 由谓词符号\(P_i\)和\(s_i\)个项\(t_j(1\leqslant j\leqslant r_i)\)构成的公示\(P_i(t_1,\cdots,t_{s_i})\)
- \(t_1=t_2\), \(t_1,t_2\)为Presburger语言的项
- 合取公式\(F_1\land F_2\)
- 析取公式\(F_1\lor F_2\)
- 逆公式\(\lnot F\)
- 存在量词公式\(\exists v:F\)
- 全称量词公式\(\forall v:F\)
Presburger算数:只有加法运算、没有乘法运算的相容且完备的公理体系
-
定义Presburger公式的语法糖,说明其它运算与加法运算间的等价性
- false \(\Leftrightarrow\) \(\lnot\)true
- \(a\Rightarrow\ \Leftrightarrow\ \lnot a\lor b\)
- \(a<b\ \Leftrightarrow\ a\leqslant b-1\), \(a\geqslant b\Leftrightarrow\ b\leqslant a\), \(a>b\ \Leftrightarrow\ a\geqslant b+1\)
- \(a,b\oplus c\ \Leftrightarrow\ a\oplus c\land b\oplus c, a\oplus_1b\oplus_2c\ \Leftrightarrow\ a\oplus_1b\land b\oplus_2c\), \(\oplus,\oplus_1,\oplus_2\in\set{<,>,=,\leqslant,\geqslant}\)
- \(-e\ \Leftrightarrow\ 0-e\), \(n\times e\ \Leftrightarrow\ e+e+\cdots e\), \(a\% n\ \Leftrightarrow\ a-n\lfloor a/n\rfloor\)
- \(n\ \Leftrightarrow\ n()\)
- 字典序:
- \(a_1,\cdots,a_n\prec b_1,\cdots,b_n\Leftrightarrow\bigvee_{i=1}^n((\bigwedge_{j=1}^{i-1}a_j=b_j)\land(a_i<b_i))\)
- \(a_1,\cdots,a_n\preccurlyeq b_1,\cdots,b_n\Leftrightarrow(a_1,\cdots,a_n\prec b_1,\cdots,b_n)\lor(a_1,\cdots,a_n=b_1,\cdots,b_n)\)
- \(a_1,\cdots,a_n\succ b_1,\cdots,b_n\Leftrightarrow b_1,\cdots,b_n\prec a_1,\cdots,a_n\)
- \(a_1,\cdots,a_n\succcurlyeq b_1,\cdots,b_n\Leftrightarrow b_1,\cdots,b_n\preccurlyeq a_1,\cdots,a_n\)
-
应用:将程序中各种操作转化为Presburger公式归纳定义中的项完成计算
true: 多维整数空间所有元素(全集)- 标量值:零维空间
Presburger公式取模表示
- 利用语法糖(5),将取模表为减法、除法
- 除法使用乘法表示
例:\(S_1(j,i)\to(j/32,i/32)\)表为\(S_1(j,i)\to(o_0,o_1):32o_0=j\land31o_1=i\)
上述表达式称为近视仿射表达式
不同维整数集合
当两个整数集合所在空间维度不一致时,两个整数集合无法进行基本的集合运算
仿射函数¶
目的:关联不同维度的整数集合
- 在集合之间构造二元映射关系:单、满、双射
整数集合映射关系:
- 访存关系:语句实例 -> 内存地址
- 调度(语句实例执行顺序):命名整数空间 -> 未命名整数空间
- 例:\(S_1(i,j)\to(i,j)\)
仿射函数
定义:形如\(f(i)=Mi+c\)的二元关系,其中\(i\in\mathbb R^d,M\in\mathbb R^{k\times d},\mathbf{c}\in\mathbb R^k\).(线性函数 + 偏移)
- 实际应用时,多面体模型将\(\mathbb R\)限制在\(\mathbb Z\)上
仿射函数集合:仿射函数构成的集合 + 约束也使用Presburger公式指定:需同时考虑定义域和值域的自由变元
分块调度
\(S_1(j,i)\to(j/32,i/32,j,i)\)
其中\((j/32,i/32)\)表示分块之间的循环维度,\((j,i)\)表示分块内的循环维度
分段形式
将不同维度映射到不同并行硬件维度上
\(\set{S_1(j,i)\to(j/32,i/32)},\set{S_1(j,i)\to(j,i)}\)
该表示称为分段近似仿射函数
集合与映射的运算¶
整数集合的运算:
- 对象:整数集合可表示一个语句的所有实例
- 化简条件:两个整数集合代表相同的语句(同构)
- 同构整数空间:\(S_1(i),T_1(j)\)同构,当且仅当
- \(S_1=T_2\)(整数空间命名相同)
- \(i=j\)(整数空间维度一致)
- 同构映射空间:两个仿射函数集合定义域、值域所在整数空间同构,则两个仿射函数集合同构
- 同构整数空间:\(S_1(i),T_1(j)\)同构,当且仅当
- 运算:以元素为单位(对整体运算 => 对每个集合运算完再组合)
- 分类:
- 单目运算:\(\odot(\cup_iR_i):=\cup_i(\odot R_i)\)
- 双目运算: \((\cup_iR_i)\oplus(\cup_jS_j):=\cup_i\cup_j(R_i\oplus S_j)\)
- 多目运算:单双目运算的组合
-
方法:利用Presburger公式的定义和语法糖
-
整数集合的并集
\[\left.S_1\cup S_2:=\left\{\begin{array}{ll}\{A(\boldsymbol{i}):p_1(\boldsymbol{i})\vee p_2(\boldsymbol{j})\},&A(\boldsymbol{i})=B(\boldsymbol{j})\\\{A(\boldsymbol{i}):p_1(\boldsymbol{i});B(\boldsymbol{j}):p_2(\boldsymbol{j})\},&\text{其他}\end{array}\right.\right.\]- \(A(\boldsymbol{i})=B(\boldsymbol{j})\)即\(S_1,S_2\)同构
-
仿射函数集合的并集
\[R_1\cup R_2:=\left\{\begin{array}{l}\{C(\boldsymbol{i}_1)\to D(\boldsymbol{j}_1):q_1(\boldsymbol{i}_1,\boldsymbol{j}_1)\vee q_2(\boldsymbol{i}_2,\boldsymbol{j}_2)\},C(\boldsymbol{i}_1)=E(\boldsymbol{i}_2)\wedge D(\boldsymbol{j}_1)=F(\boldsymbol{j}_2)\\\\\{C(\boldsymbol{i}_1)\to D(\boldsymbol{j}_1):q_1(\boldsymbol{i}_1,\boldsymbol{j}_1);E(\boldsymbol{i}_2)\to F(\boldsymbol{j}_2):q_2(\boldsymbol{i}_2,\boldsymbol{j}_2)\},\quad\text{其他}\end{array}\right.\]- \(C(\boldsymbol{i}_1)=E(\boldsymbol{i}_2)\wedge D(\boldsymbol{j}_1)=F(\boldsymbol{j}_2)\)即\(R_1,R_2\)同构
-
整数集合的交集
\[S_1\cap S_2:=\left\{\begin{array}{ll}\{A(\boldsymbol{i}):p_1(\boldsymbol{i})\wedge p_2(\boldsymbol{j})\},&A(\boldsymbol{i})=B(\boldsymbol{j})\\\varnothing,&\text{其他}\end{array}\right.\] -
仿射函数集合的交集
\[\left.R_1\cap R_2:=\left\{\begin{array}{ll}\{C(\boldsymbol{i}_1)\to D(\boldsymbol{j}_1):q_1(\boldsymbol{i}_1,\boldsymbol{j}_1)\wedge q_2(\boldsymbol{i}_2,\boldsymbol{j}_2)\},&C(\boldsymbol{i}_1)=E(\boldsymbol{i}_2)\wedge D(\boldsymbol{j}_1)=F(\boldsymbol{j}_2)\\\\\emptyset,&\text{其他}\end{array}\right.\right.\] -
整数集合的差集
\[\left.S_1\setminus S_2:=\begin{cases}&\{A(\boldsymbol{i}):p_1(\boldsymbol{i})\wedge\neg p_2(\boldsymbol{j})\},&A(\boldsymbol{i})=B(\boldsymbol{j})\\&\{A(\boldsymbol{i}):p_1(\boldsymbol{i})\},&\text{其他}\end{cases}\right.\] -
仿射函数集合的差集
\[\left.R_1\backslash R_2:=\left\{\begin{array}{ll}\{C(\boldsymbol{i}_1)\to D(\boldsymbol{j}_1):q_1(\boldsymbol{i}_1,\boldsymbol{j}_1)\wedge\neg q_2(\boldsymbol{i}_2,\boldsymbol{j}_2)\},&C(\boldsymbol{i}_1)=E(\boldsymbol{i}_2)\wedge D(\boldsymbol{j}_1)=F(\boldsymbol{j}_2)\\\\\{C(\boldsymbol{i}_1)\to D(\boldsymbol{j}_1):q_1(\boldsymbol{i}_1,\boldsymbol{j}_1)\},&\text{其他}\end{array}\right.\right.\] -
包含关系:转化为上述运算
- \(A\subseteq B\Leftrightarrow A\backslash B=\varnothing\)
- \(A\supseteq B\Leftrightarrow B\subseteq A\)
- \(A=B\Leftrightarrow A\subseteq B\land B\subseteq A\)
- \(A\subset B\Leftrightarrow A\subseteq B\land\lnot(A=B)\)
- \(A\supset B\Leftrightarrow B\subset A\)
-
- 分类:
基数(单目运算)
整数集合和仿射函数集合绝大部分定义、运算规则相同,但==基数定义不同==
整数集合\(\set{S(i):p(i)}\)
- \(\text{card}\ S:=\set{\#i:p(i)}\) (满足约束的元素个数)
仿射函数集合\(\set{S(i)\to T(j):p(i,j)}\)
- \(\text{card}\ S:=\set{S(i)\to\#T(j):p(i,j)}\) (定义域对应像的个数)
- 应用:判定单射满射
Fourier-Motzkin 消去法¶
目的:不等式组消元
原理:对于不等式组\(A_{m\times n}x\leqslant b,\ x\in\mathbb R^n,b\in\mathbb R^m\) ,记\(A_{m\times n}\)行向量为\(a_1^\mathrm T,\cdots,a_m^\mathrm T\),则不等式组可改写为
给定一系列非负整数\(\lambda_1,\lambda_2,\cdots,\lambda_m\),有
通过选择合适的\(\lambda_1,\lambda_2,\cdots,\lambda_m\)使得某个变量\(x_i\)系数为0,从而消去\(x_i\)
步骤:记所有不等式构成的集合为\(S\),涉及\(x_i\)的不等式构成的集合为\(C_i\),其中
- 下界约束集合\(L_i\):形如\(l_j\leqslant c_1x_i\)约束构成的集合
- 上界约束集合\(U_i\):形如\(c_2x_i\leqslant u_k\)约束构成的集合
故\(C_i=L_i\cup U_i\)
- \(\forall l\in L_i,\forall u\in U_i,\ l\leqslant c_1x_i,\ c_2x_i\leqslant u\)
- 记\(v=[c_1,c_2]\),构造\(\dfrac{v}{c_2}l\leqslant\dfrac{v}{c_1}u\)
构造出来不包含\(x_i\)的不等式构成集合\(C^/{}_i\),得消去\(x_i\)的不等式集合\(S^/=(S\setminus C_i)\cup C^/{}_i\),\(S^/\)与\(S\)等价(即\(S\)有解\(\ \Leftrightarrow\ S^/\)有解)
性质:
- \(|C^/{}_i|=|U_i|\times|L_i|\)
- \(|U_i|+|L_i|=|C_i|\leqslant m\Rightarrow|C^/{}_i|\leqslant\left\lfloor\dfrac{m^2}{4}\right\rfloor\)(基本不等式)
- 与多面体的关系:从\(S=\set{x\in\mathbb R^n:Ax\leqslant b}\)中消去\(x_m\),相当于求\(S\)在平面\(S_m=\set{x\in\mathbb R^n:x_m=0}\)的投影\(P_m(S)\)
- \(P_m(S)\)是\(x_m\)在取满足\(S\)约束的任意合法值的前提下,剩余\(n-1\)个变量之间的约束
- \(P_m(S)\)仍为多面体,\(P_m(S)\)的面对应\(S\)的面,\(P_m(S)\)每个顶点对应\(S\)某些顶点在\(S_m\)的投影
- 若\(S\)有\(m\)个面,则\(P_m(S)\)至多有\(\left\lfloor\dfrac{m^2}{4}\right\rfloor\)个面(约束 <=> 面)
- 去除冗余约束后得到的\(P'm(S)\)仍是多面体(合法的不等式组)
投影 VS 求交
投影:将原多面体\(S\)的一对面关于\(x_m\)的分量相互抵消,组合成\(P_m(S)\)的面
- 例:3维面 => 2维直线
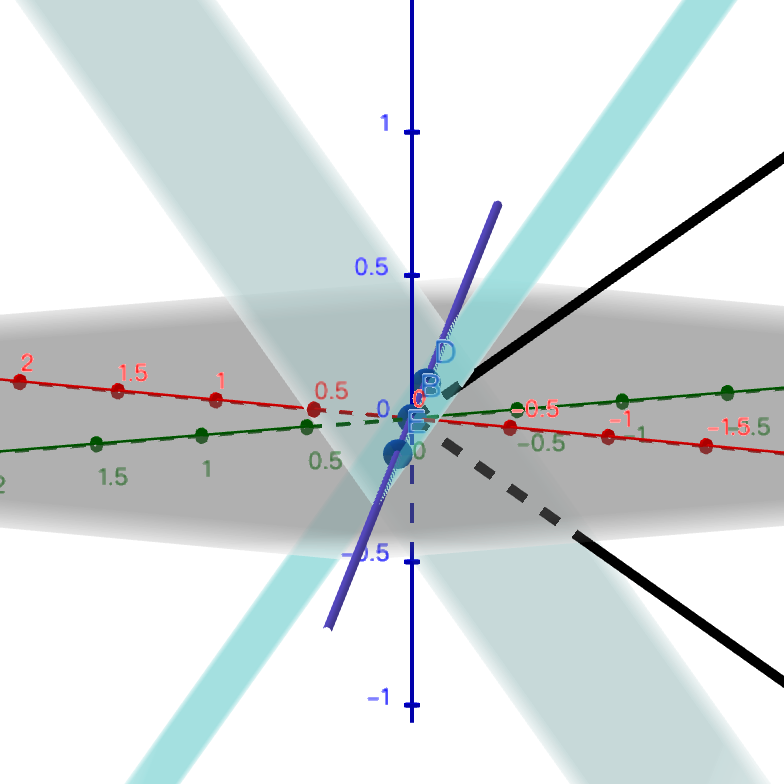
交:将原多面体\(S\)的一个面与\(S_m\)联立
- 投影 \(\not=\) 求交,即\(x_m\)可去任意合法值,而不是令\(x_m=0\)
- 投影依赖于投影对象与投影平面的距离,而单个平面与投影平面相交,无距离概念,故只有平面对可以进行投影
Fourier-Motzkin 消去法示例
对于不等式组
改写为
两两组合,消去\(x\)
循环上下界计算:
// 1. 从最内层开始逐层消去
S[N] = S;
for (i = N; i >= 1; i--) {
/* S[i]与x[1], ..., x[i]有关 */
// 从S[i]中选取涉及x[i]的上界集合U[i], 消除冗余, 得到U'[i]
// 从S[i]中选取涉及x[i]的下界集合L[i], 消除冗余, 得到L'[i]
// 利用Fourier-Motzkin消去法将x[i]从S[i]消去, 得到S[i-1]
}
// 2. 从最外层开始逐层精简
/*
由静态仿射约束知, 内层循环上下界可包含外层循环变量;
而U'[i], L'[i]与x[1], ..., x[i]有关, 满足要求
*/
for (i = 1; i <= N; i++) {
// 消除U'[i]中冗余约束(此时U'[i]已完成求解), 更新U'[i+1], ..., U'[N]
// 消除L'[i]中冗余约束, 更新L'[i+1], ..., L'[N]
}
调度的表示¶
原始调度:初始时语句执行顺序(程序在文本中出现的顺序)
- 编译优化的目的:(基于程序的依赖关系)计算新的调度
- 代码生成:调度树 -> AST
调度表示的要求:既要支持原始程序语句调度的表示,又要能表示经过调度变换后语句的执行顺序
- 同时支持调度变换前后的输入输出
调度表示:
- 仿射函数表示:用于表示含有一个语句的一个循环嵌套
- 循环嵌套间:无法确定语句的先后顺序(仿射函数未提供语句属于不同循环嵌套的信息)
- 循环嵌套内:同一循环嵌套内的语句先后顺序不明确
- Kelly表示:在仿射函数值域中引入标量维度
- 2d+1表示:外层循环索引变量(d个)和标量(d+1个)相间
- union map表示:对Kelly表示做0填充,使得所有仿射函数维度都与最大的函数维度一致
- 调度树表示:与Kelly表示,2d+1表示和union map表示表达能力相同,更直观
- 将迭代空间和调度封装在一起
调度表示示例
for (i = 0; i < M; i++)
a[i] = i; // S1
for (i = 0; i < M; i++) {
for (j = 0; j <= N; j++)
c[i] += b[i][j] * a[i]; // S2
d[i] = c[i]; // S3
}
- 解释:
- 第一维表示\(S_1\)与\(S_2,S_3\)嵌套循环之间的先后顺序
- 可理解为最外层存在虚拟的外层循环
- 第三维表示\(S_2\)与\(S_3\)在相同嵌套循环内的先后顺序
- 相同循环嵌套内,不同语句的仿射函数值域维度也可不同
- 第一维表示\(S_1\)与\(S_2,S_3\)嵌套循环之间的先后顺序
- 问题:每个语句对应的仿射函数值域维度并不完全相同,比较不同语句实例之间的执行顺序不方便
2d+1表示:\(\set{(i)\to(0,i,0)};\set{(i,j)\to(1,i,0,j,0)};\set{(i)\to(1,i,1)}\)
- 解释:
- 每个标量表示前一个循环索引变量对应循环内该语句的执行顺序
- 最左端的标量代表所有循环嵌套的执行顺序
- 问题:由于矩阵维度固定,无法直接表示循环分块等改变嵌套维度的变换
union map表示:\(\set{S_1(i)\to(0,i,0,0)};\set{S_2(i,j)\to(1,i,0,j)};\set{S_3(i)\to(1,i,1,0)}\)
- 允许不同语句的仿射函数之间进行严格的字典序比较
- 对仿射函数进行命名
调度树表示:
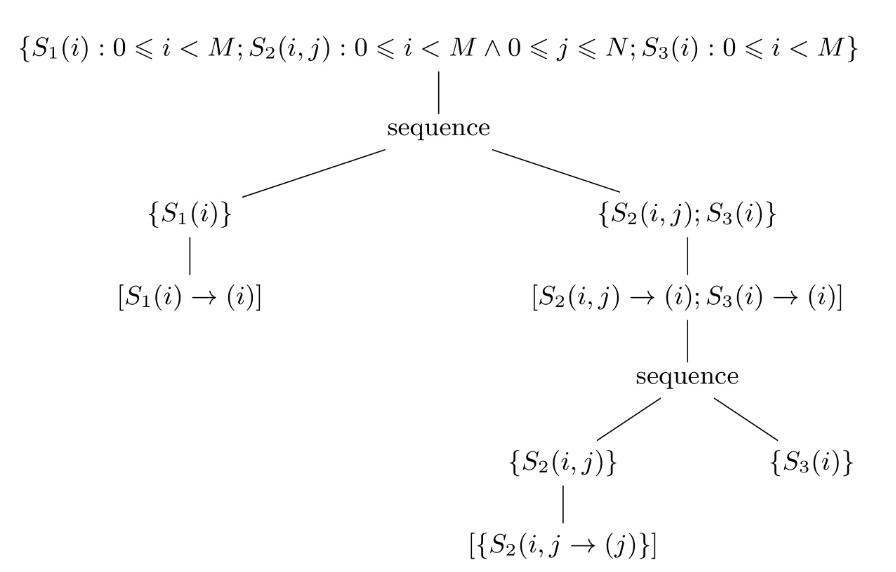
调度表示评估:
- 调度对象粒度:语句 / 片段
- 局部调度表示:仿射 / 近似仿射
- 标量维度表示:显式sequence结点 / 标量相对大小
- 多语句组合调度:能否携带领域特定信息
- 单射函数支持:语句间并行(不同语句实例在同一时刻执行)
- 满射函数支持:一个语句实例被多次执行
- 偏序关系比较:严格 / 非严格
调度树¶
结点类型:
- domain结点:调度树根结点,表示迭代空间(程序语句实例集合)
- 表示:命名整数集合的并集
- 一个命名整数集合代表一个独立的语句
- 表示:命名整数集合的并集
- context结点:编译符号常量(全局/局部)及其约束
- 性质:
- context结点引入的符号常量只能在后继子树上使用
- 当context是domain结点的子结点,且只包含全局符号常量时,可省略
- 性质:
- band结点:表示其父结点内语句实例的调度(可对应循环嵌套)
- 性质:
- 作为 domain / filter / extension / expansion 结点的子结点
- 可以有多个member, 每个成员对应循环嵌套的一个循环维度
- 表示:仿射集合的并集,使用
[]封装 - 属性:
- permutable
bool:循环嵌套每个循环维度相互交换是否合法 - coincident
Array[bool]:对应循环维度是否可以并行执行 - 代码生成控制选项:分块分离、循环展开
- permutable
- 性质:
- sequence结点:表示标量维度
- 性质:
- 可有多个子结点,子结点从左往右按序执行
- 子结点只能是filter结点
- 性质:
- set结点:子结点可以任意顺序执行的sequence结点(可以有多个filter子结点)
- filter结点:过滤domain结点封装的不同整数集合
- 性质:
- 作为sequence / set结点的子结点
- 也可过滤expansion / extension / filter 结点
- 不能作为调度树的根结点出现
- 作为sequence / set结点的子结点
- 表示:整数集合的并集
- 性质:
- mark结点:向调度树插入任意信息,用于代码生成
- 表示:字符串
- extension结点:向调度树添加没有被domain结点覆盖的语句(生成特殊指令)
- 性质:特殊情况可作根结点
- 表示:仿射函数集合的并集
- expansion结点:对循环嵌套内的语句进行组合
- 表示:仿射函数集合的并集
- 定义域:被过滤到当前结点的语句实例集合
- 映射到新语句实例集合上
- 表示:仿射函数集合的并集
- guard结点:描述编译符号常量和外层band结点对应的循环索引变量对当前子树的约束
- leaf结点:表示调度树的分支终点(不包含任何信息)
- 性质:无子结点
生成:
- 合并多个不同子树
- 结点操作
操作:
- 插入 context / filter / mark 结点:引入额外的局部符号常量 / 对并集内的不同集合独自处理 / 嵌入额外信息
- 修改 band 结点:实现幺模变换、循环分块、循环分段等循环变换
- 分裂 band 结点:软件循环 -> 硬件,分裂后结点为父子关系
- permutable 属性不变,coincident 维度变小,分量值不变
- 组合 band 结点:分裂的逆过程
- 融合 band 结点:调度算法计算(算子融合)
- 分布 band 结点:融合逆过程
- 分块 band 结点:修改band结点的仿射函数,实现循环分块
- 下沉 band 结点:与分裂配合使用
- 例:面向GPU生成时,分裂band,外层band映射到不同block内,内层band下沉到filter后,将filter结点对应的计算映射到不同thread组内
- 重排序 sequence 结点:优化执行顺序