量子游走

量子游走最初作为经典随机游走算法的量子版本而研究，是构建量子算法的有力工具。

量子游走的随机性体现在测量读出结果的随机而非确定性的演化，故很少说Quantum Random Walks，游走过程是确定性的，该名称自相矛盾。

量子游走根据时间的连续性或是否使用硬币分为两个基本模型：离散时间量子游走 (DTQW) 和连续时间量子游走 (CTQW)，两个模型互相独立，不能相互推出。

两模型不等价的证据：

两个模型在格点上的空间搜索问题具有不同的时间复杂度

在二维具周期性边界格点上的标记点搜索问题中，DTQW较于CTQW存在二次加速

量子情形下，在远离原点处找到游走者的概率更大，这也是量子游走效率高于经典算法的主要原因。

经典随机游走¶

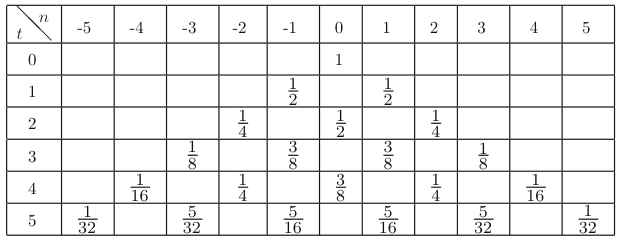
经典线上随机游走：游走者最初（$t=0$）位于$n=0$处，每次抛掷一枚无偏硬币，若硬币反面朝上，游走者向右走一个单位；若硬币正面朝上，则向左走一个单位。由于$t$时刻游走者位置未知，用概率进行刻画，故$p(t=0,n=0)=1$, $p(t,n)=\dfrac{1}{2}p(t-1,n-1)+\dfrac{1}{2}p(t-1,n+1)$.

通项：$p(t,n)=\dfrac{1}{2^t}C_t^{\frac{t+n}{2}}$

$p(t,n)\not=0$条件:

$n,t$奇偶性相同

$-t\leqslant n\leqslant t$

概率分布表	概率分布图

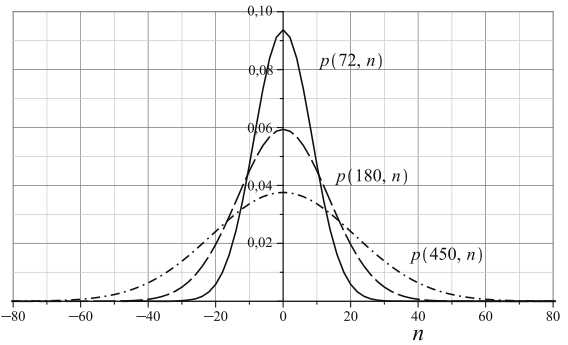绘制概率分布图时，用$p(t,n)+p(t+1,n)$替代$p(t,n)$消除折线，得到曲线

性质：

随着$t$增加，最高点逐渐降低，宽度逐渐增大
对称分布，期望距离$\langle n\rangle=\sum\limits_{n=-\infty}^\infty np(t,n)=0$
标准差$\sqrt{\langle n^2\rangle-\langle n\rangle^2}=\sqrt{\sum\limits_{n=-\infty}^\infty n^2p(t,n)}=\sqrt t$，正比于$\sqrt{t}$

另解：利用Stirling近似：$t!\approx \sqrt{2\pi t}\ t^t\ e^{-t}$

$p(t,n)\simeq\dfrac{2}{\sqrt{2\pi t}}e^{-\frac{n^2}{2t}}$，$t$为大数时近似为正态分布

标准差即为正态曲线的宽度，即拐点距离的一半，为$\sqrt t$

离散时间量子游走 (DTQW)¶

经典离散 Markov 链¶

经典 Markov 链定义在离散状态集上，链的次态仅仅取决于现态，与先前状态无关。可视作有向图，顶点表示状态，有向边表示次态的转移。

Markov 链状态集离散，离散 / 连续 Markov链指演化时间的连续性

形式化定义：设图$\Gamma(X,E)$，顶点集$X=\set{x_1,\cdots,x_n}$，$|X|=n$，边集$E$，概率分布由向量$\begin{bmatrix}p_1(t)\\\vdots\\p_n(t)\end{bmatrix}$描述，其中$p_i(t)$为$t$时刻游走者位于顶点$x_i$的概率。设转移矩阵为$M=(m_{ij})_{n\times n}$，其中$m_{ij}$为$x_i$转移至$x_j$的概率，则 $$ p_i(t+1)=\sum_{j=1}^nm_{ij}p_j(t) $$ 写作向量形式：$\vec{p}(t+1)=M\vec{p}(t)$，$M$又称左随机矩阵；递推得$\vec{p}(t)=M^t\vec p(0)$

由于$\vec p$为概率分布，故$M$满足 (1) 非负实矩阵 (2) 列和为1

当图无向且向相邻顶点等可能转移时，$m_{ij}=\dfrac{1}{d_j}$，其中$d_j$为$x_j$的度；进而$m_{ij}=a_{ij}/d_j$，其中$A$为图的邻接矩阵。

下以无向完全图为例：

\[ M=\dfrac{1}{n-1}\begin{bmatrix} 0&1&1&\cdots&1\\ 1&0&1&\cdots&1\\ 1&1&0&\cdots&1\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 1&1&1&\cdots&0 \end{bmatrix},\quad \vec p(0)=\begin{bmatrix} 1\\0\\\vdots\\0 \end{bmatrix} \]

\[ \Rightarrow\vec p(t)=\begin{bmatrix} f_n(t-1)\\ f_n(t)\\ \vdots\\ f_n(t) \end{bmatrix},\quad f_n(t)=\dfrac{1}{n}\left(1-\dfrac{1}{(1-n)^t}\right) \]

当$t\to\infty$时，极限分布为均匀分布。

DTQW¶

量子化：$\mathcal H=\mathcal H_c\otimes \mathcal H_p$

位置：用计算基$\set{\ket{n}:n\in\mathbb Z}$表示，张成$\mathcal H_p$
硬币算子$C$：作用于空间$\mathcal H_C=\mathcal L(\ket0,\ket1)$的任意2维酉矩阵
转移算子$S$：根据硬币指示更新游走者空间位置，0右移、1左移

\[ \left\{ \begin{array}{l} S\ket0\ket n=\ket0\ket{n+1}\\ S\ket1\ket n=\ket1\ket{n-1} \end{array} \right. \]

可综合为$S=\ket0\bra0\otimes\sum\limits_{n=-\infty}^\infty\ket{n+1}\bra n+\ket1\bra1\otimes\sum\limits_{n=-\infty}^\infty\ket{n-1}\bra n$

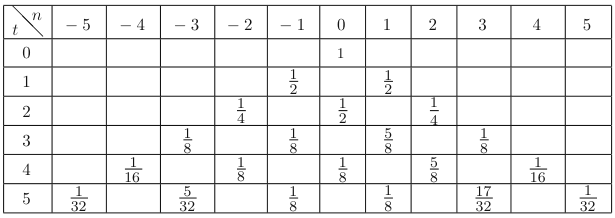
取初态$\ket{\psi(0)}=\ket0\ket{n=0}$.游走时，先作用硬币算子，即作用$C\otimes I$，再作用$S$，达到所需轮数后对系统进行测量。

下取使用1维情形下使用最广的无偏硬币$H$.

$H\ket0=\dfrac{1}{\sqrt2}(\ket0+\ket1),\ H\ket1=\dfrac{1}{\sqrt2}(\ket0-\ket1)$，符号不影响测量的概率大小，故称$H$为无偏硬币

一次游走可写为$U=S(H\otimes I)$，则$\ket{\psi(t)}=U^t\ket{\psi(0)}$.

概率分布表	概率分布图

概率的数值计算方法：

递推：设通项$\ket{\psi(t)}=\sum\limits_{n=-\infty}^\infty(A_n(t)\ket0+B_n(t)\ket1)\ket n,\ \sum\limits_{n=-\infty}^\infty|A_n(t)|^2+|B_n(t)|^2=1$

作用$S(H\otimes I)$得：

\[ \left\{ \begin{array}{l} A_n(t+1)=\dfrac{A_{n-1}(t)+B_{n-1}(t)}{\sqrt2}\\ B_n(t+1)=\dfrac{A_{n+1}(t)-B_{n+1}(t)}{\sqrt2} \end{array} \right. \]

边界条件：$A_n(0)=\left\{\begin{array}{l}1,&n=0,\\0,& \text{otherwise}\end{array}\right.$, $B_n(0)=0$

$p(t,n)=|A_n(t)|^2+|B_n(t)|^2$

直接计算$U$：由于$t$时刻$\ket{\psi(t)}$中非零元有限，可限制$U$的维度，从而计算$U^t\ket{\psi(0)}$

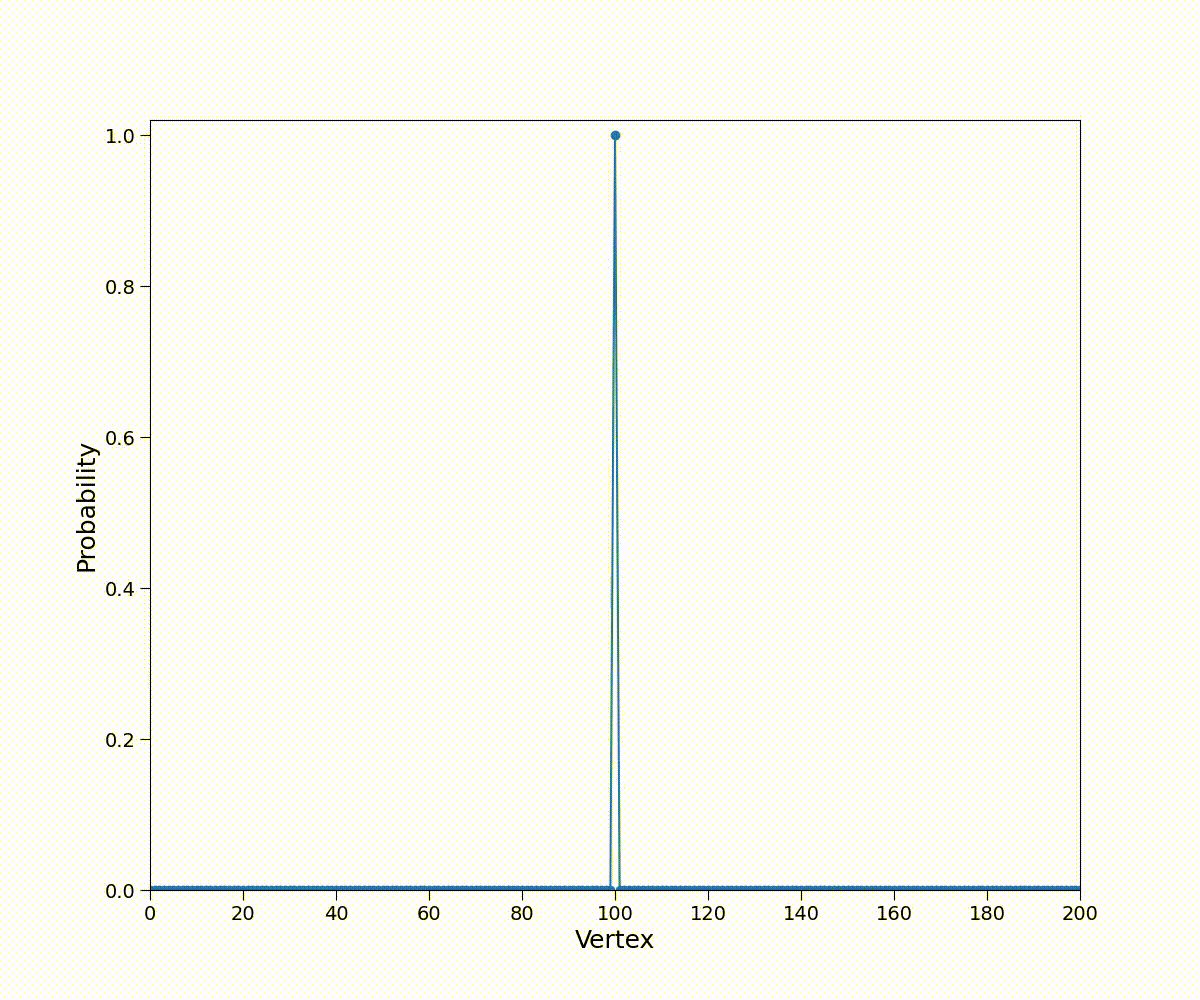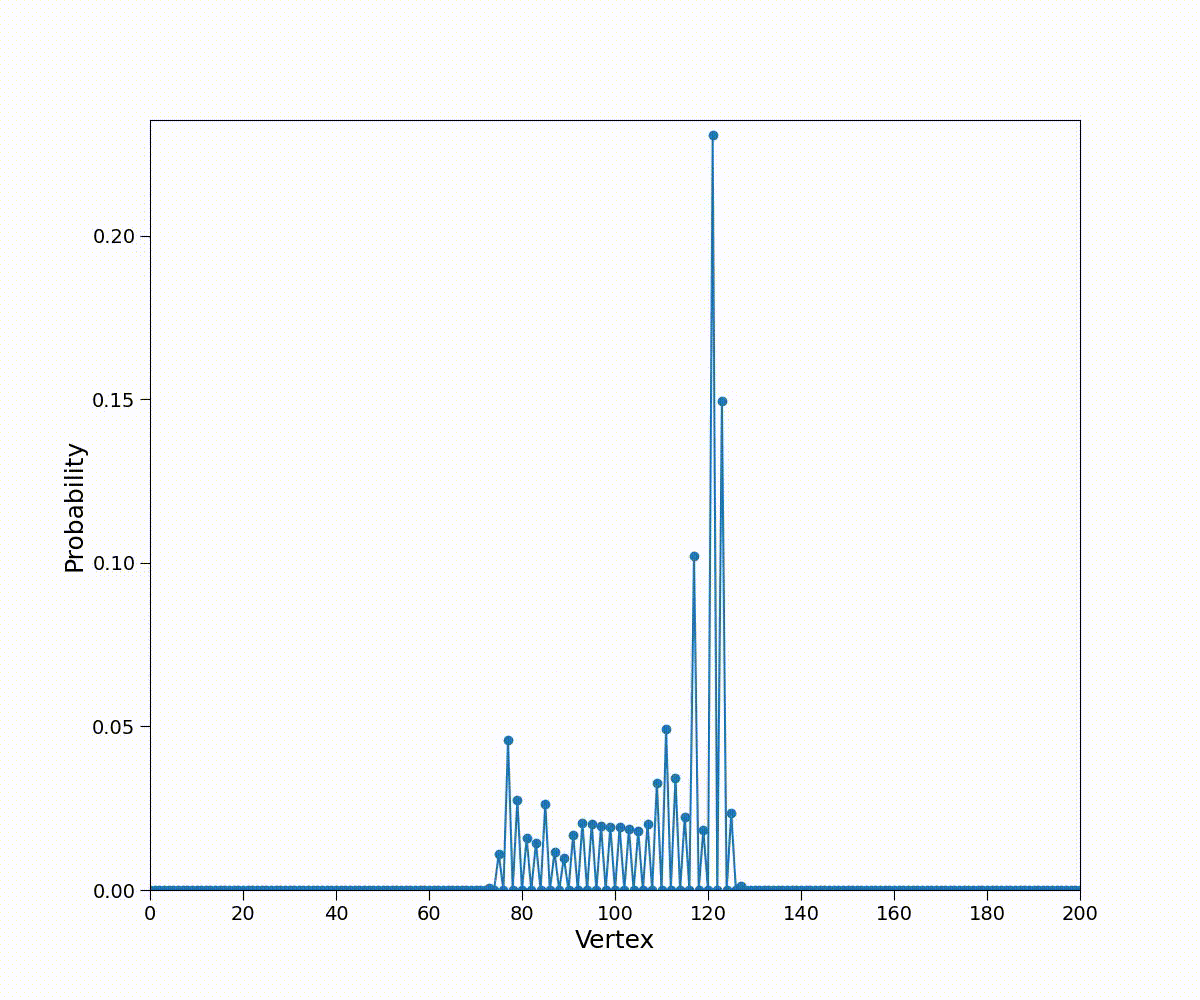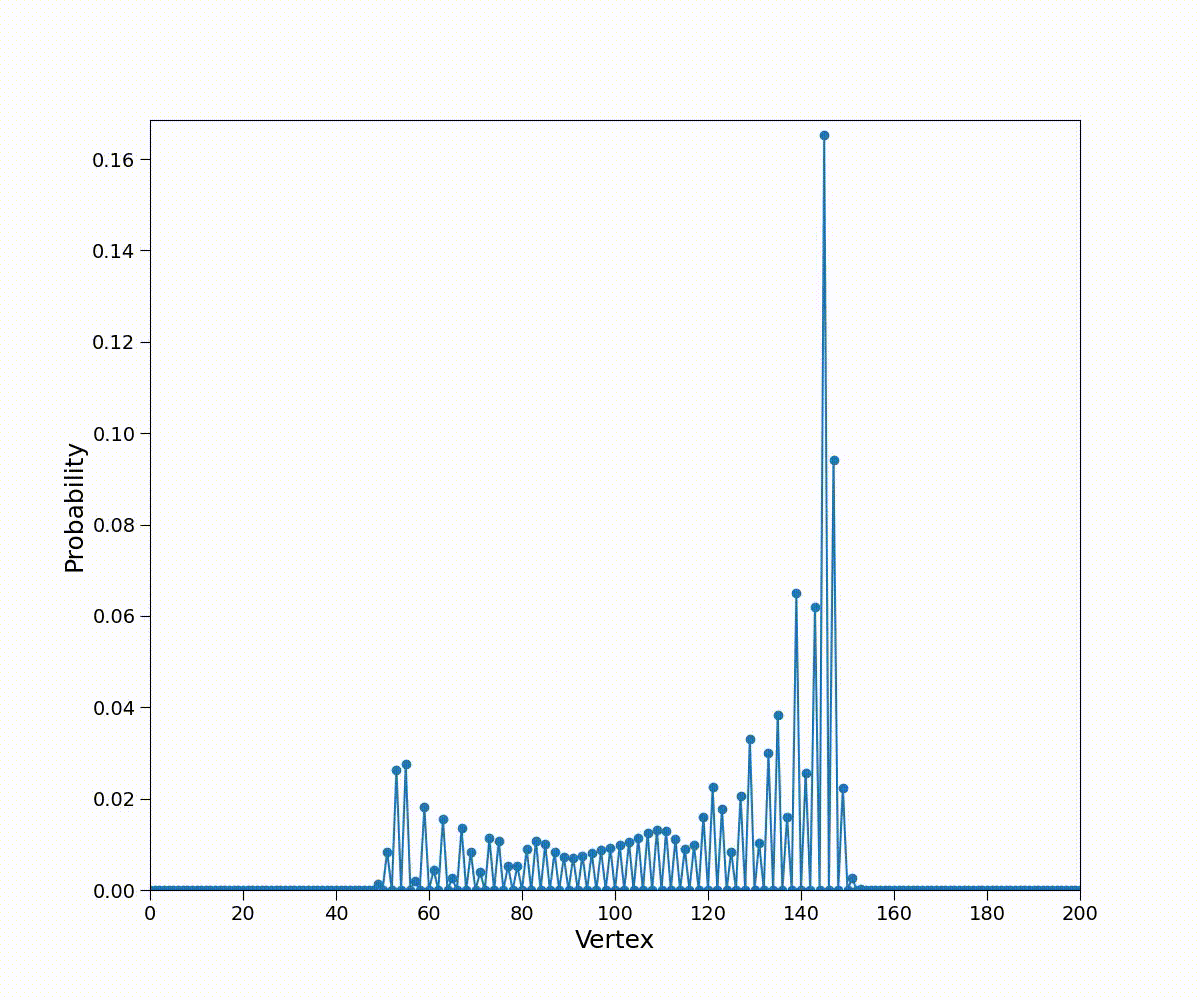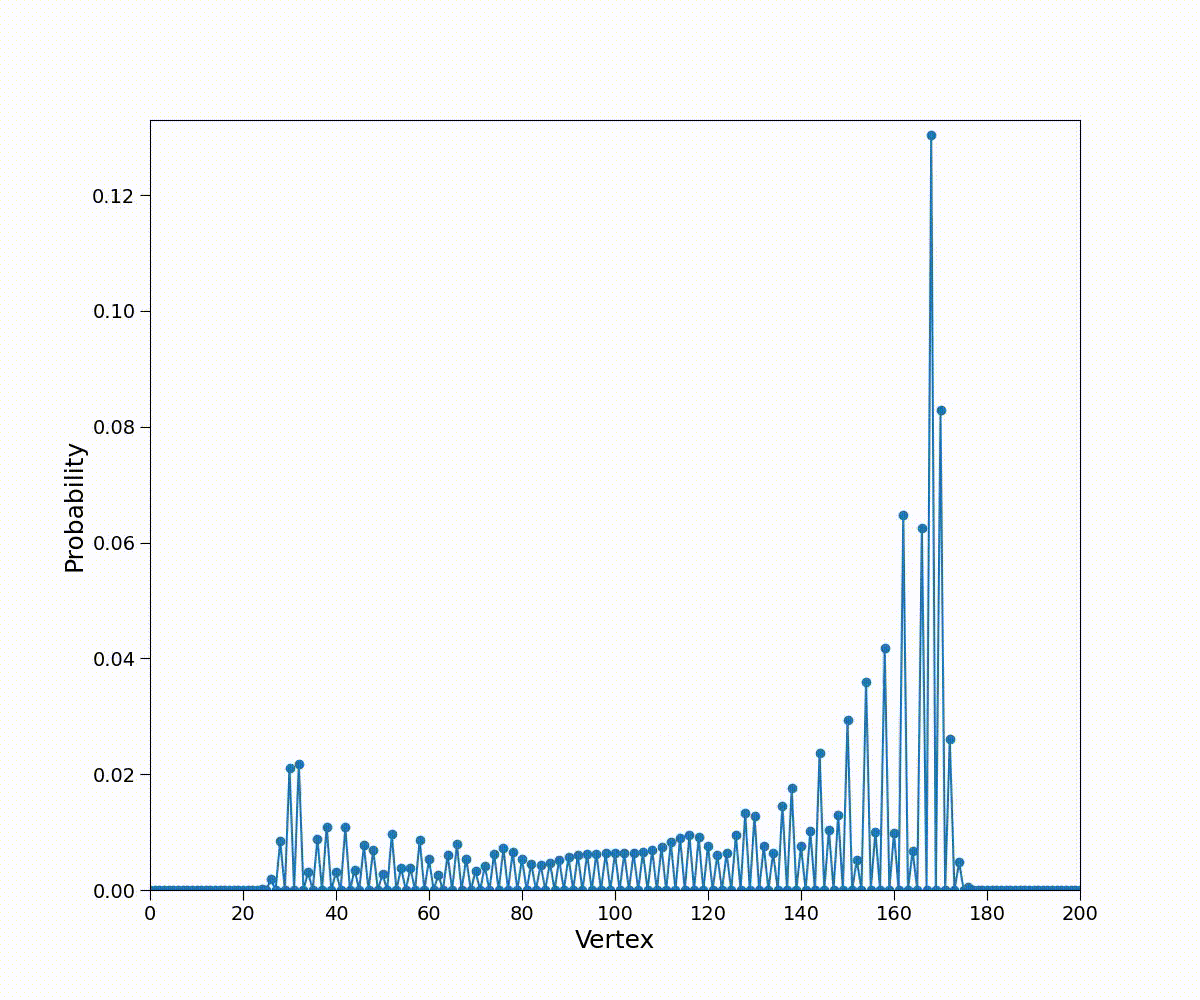
分布不对称的原因：$H\ket 1$产生负号，导致$\ket1\ket n$前的系数被抵消，而$\ket1$指示向左移动，故整体向右移动。同理，若取$\ket{\psi(0)}=-\ket1\ket{n=0}$，将与取$\ket{\psi(0)}=\ket0\ket{n=0}$得到的结果呈镜像。

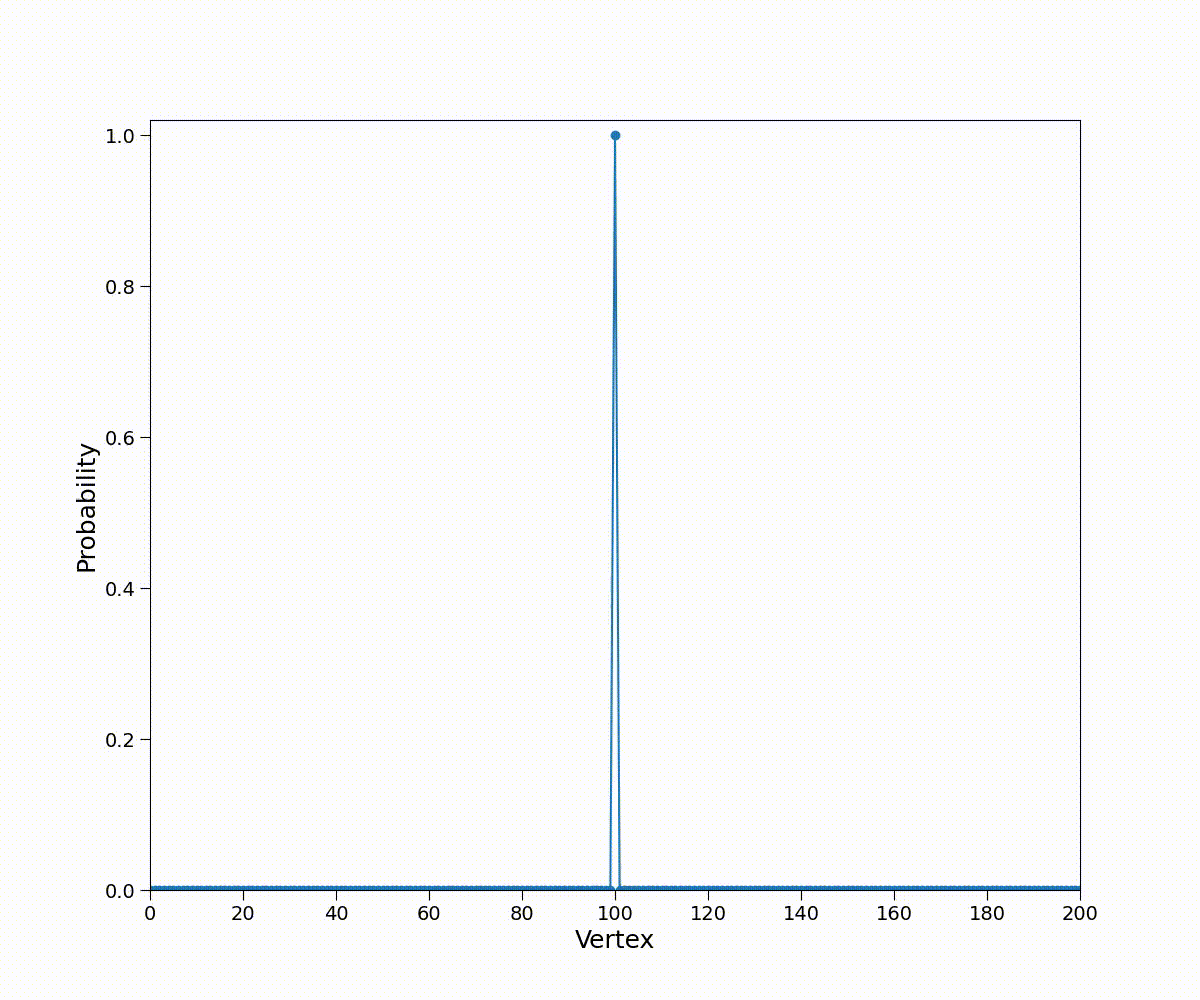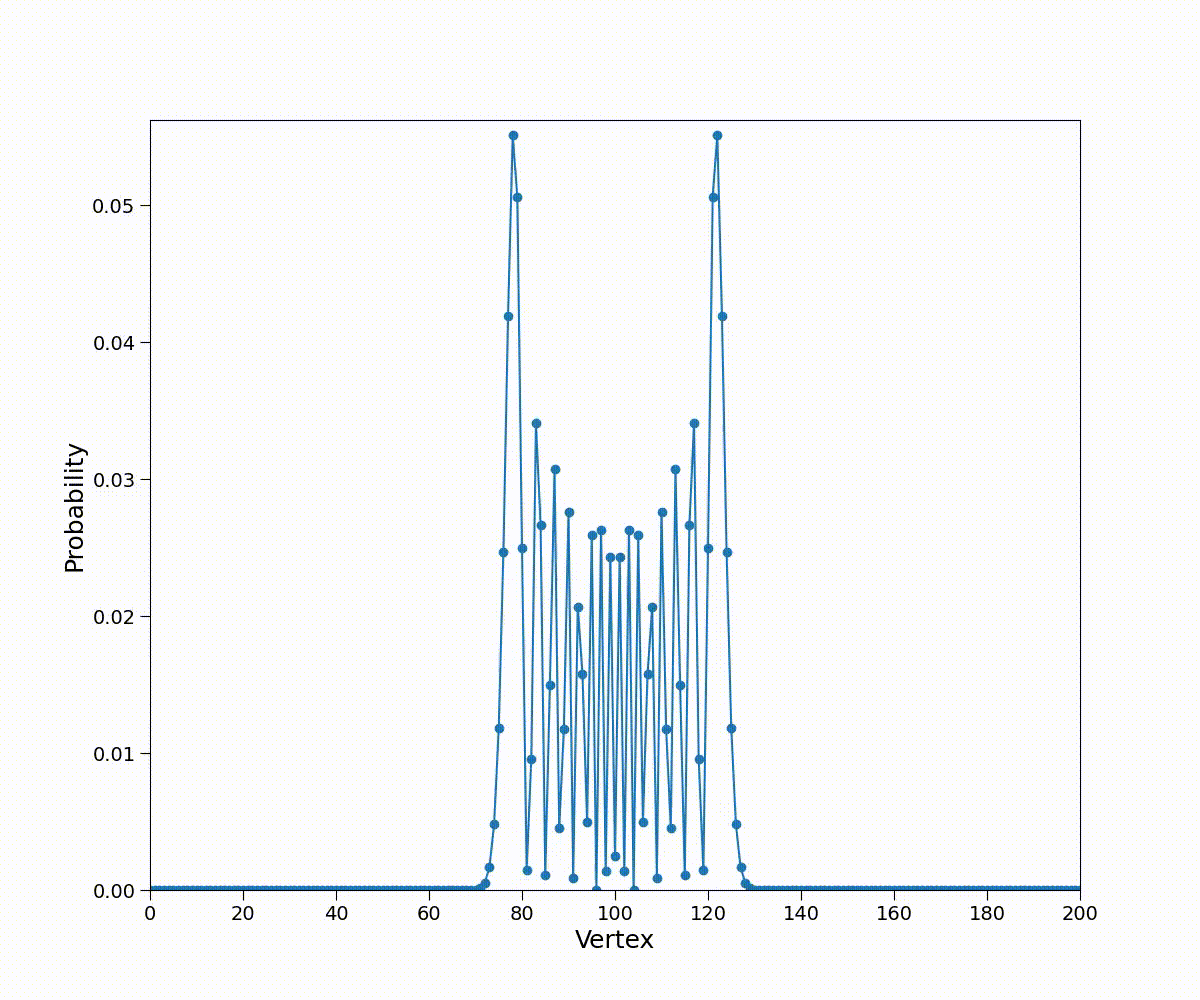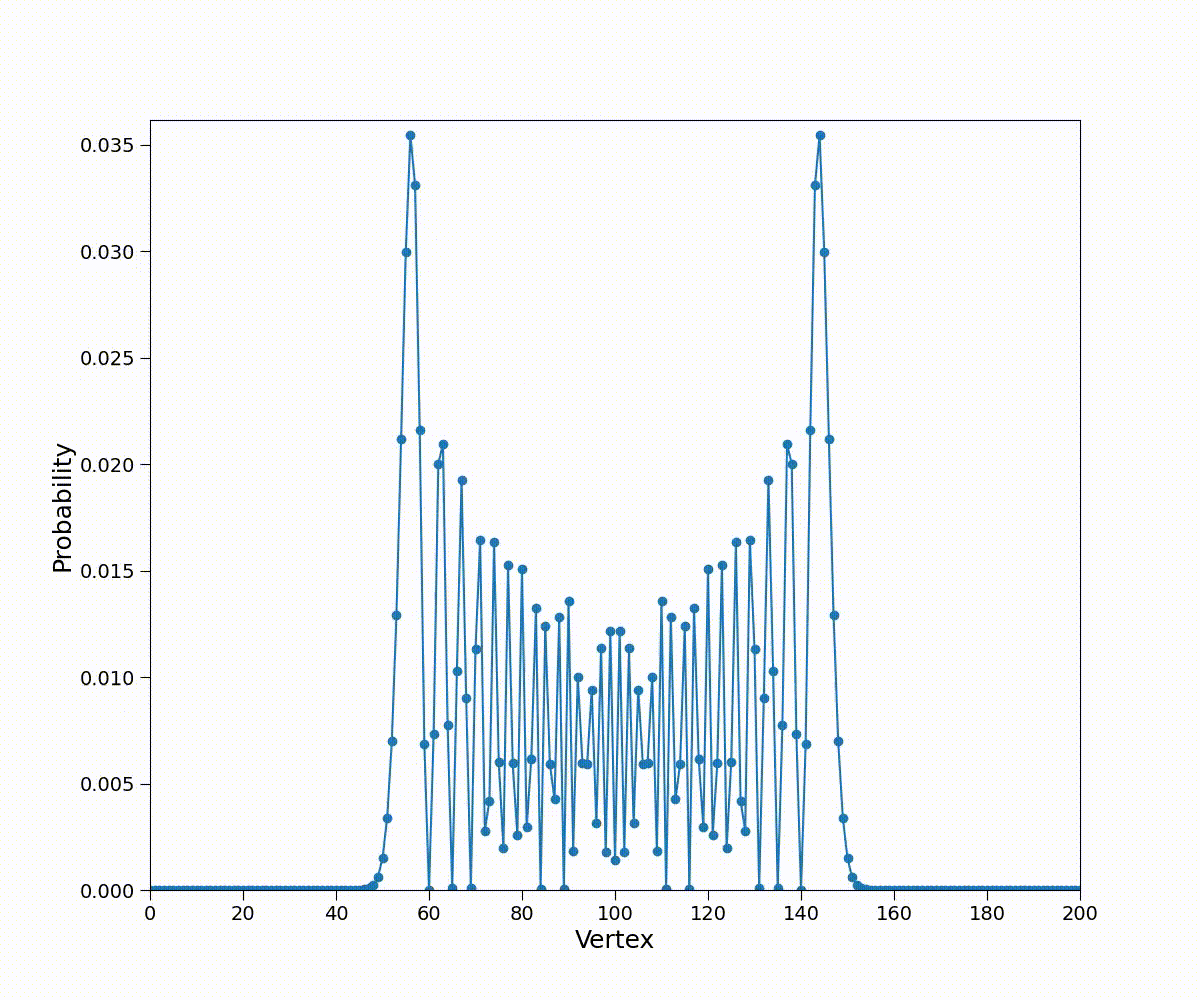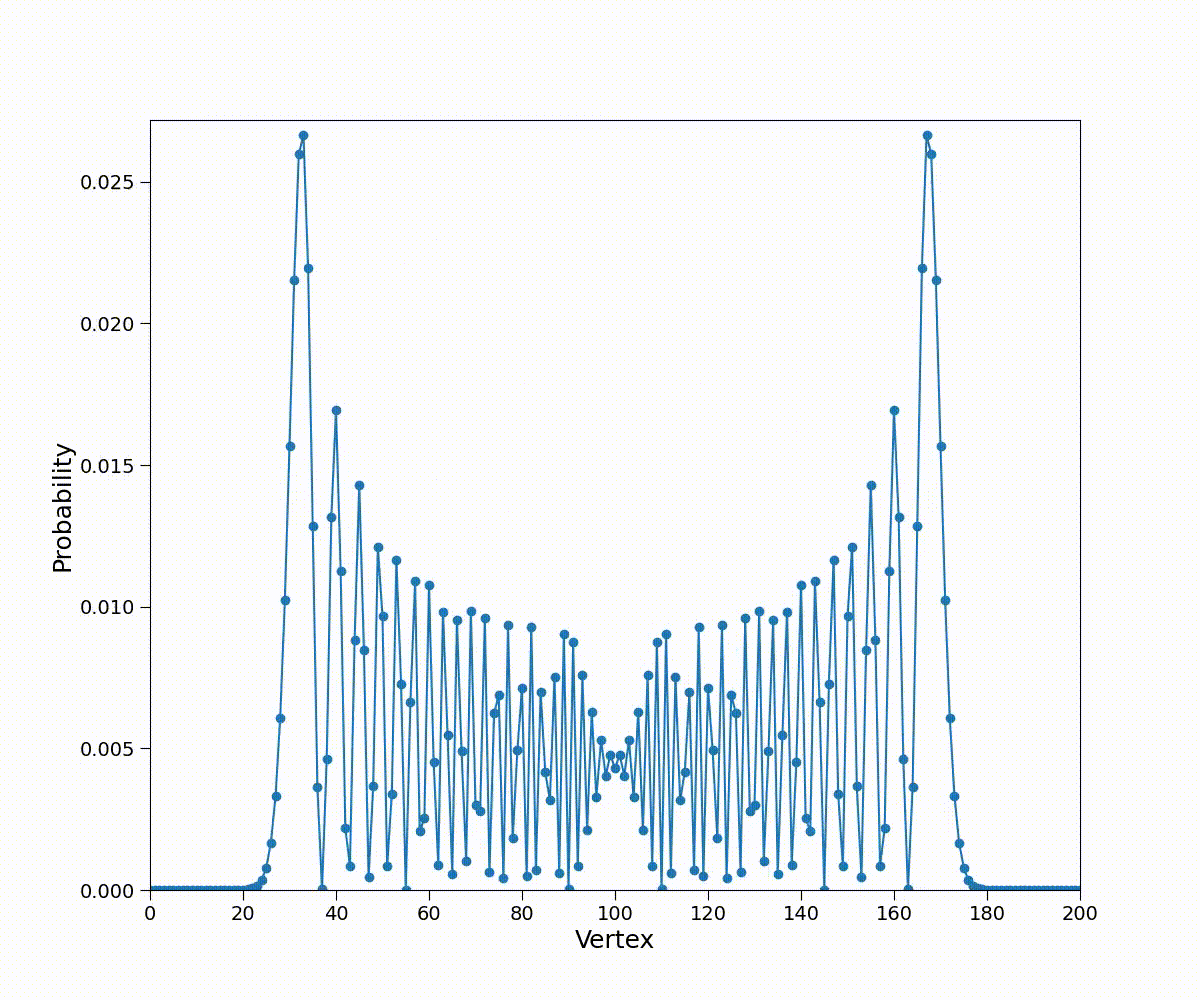
故只需将二者叠加，便能产生对称分布；为了不相互抵消，由于$H$不产生复数贡献，故引入复数进行叠加，取$\ket{\psi(0)}=\dfrac{\ket0-i\ket1}{\sqrt2}\ket{n=0}$，概率分布如下

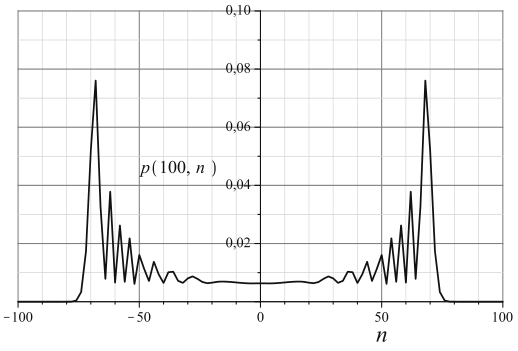
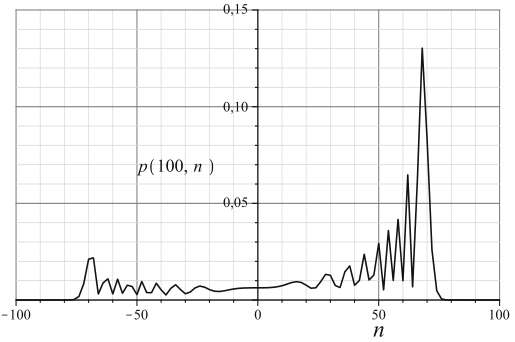
性质：

对称，$\langle n\rangle=0$
标准差$\sigma(t)=\sqrt{\sum\limits_{n=-\infty}^\infty n^2p(t,n)}\approx0.54t\propto t$

与经典随机游走的区别：

具有弹道运动的特性：当游走者从原点出发向右做速度为1的匀速直线运动时，$p(t,n)=\delta_{tn}$此时$\sigma(t)=t$
概率分布在$[-t/\sqrt2,t/\sqrt2]$，而不是聚集在原点

使用hiperwalk进行模拟：

import hiperwalk as hpw

N = 201
line = hpw.Line(N)     # 建图
qw = hpw.Coined(line)  # 建立DTQW模型
vertex = N // 2
initial_state = qw.ket(vertex, vertex + 1)  # 游走者位置, 次态

final_state = qw.simulate(time=(N // 2, 1), initial_state=initial_state)
probability = qw.probability_distribution(final_state)
hpw.plot_probability_distribution(probability, animate=True, plot='line', rescale=True)

连续时间量子游走 (CTQW)¶

经典连续 Markov 链¶

与离散 Markov 链的不同，连续情形下不使用硬币，同时时间从原来的离散型随机变量变为连续型随机变量；游走者可以在任意时刻从$x_j$游走至$x_i$. 可将其视作水流，$x_j$处的液体流至$x_i$处，随着时间的推移，留在$x_j$的概率逐渐减小，在$x_j$邻居处发现的概率逐渐增大。

引入转移率$\gamma$，表示相邻节点在单位时间内转移的概率。下假设对于整张图而言$\gamma$为常数，建立相应的微分方程。

在$\epsilon$时间内，游走者从$x_j$转移至相邻节点$x_i$的概率为$\gamma\epsilon$. 设$x_j$的度数为$d_j$，那么转移至相邻节点的概率为$d_j\gamma\epsilon$，留在$x_j$的概率为$1-d_j\gamma\epsilon$.

设转移矩阵为$M(t)$，代表$t$时刻的转移概率，则

\[ m_{ij}(\epsilon)=\left\{ \begin{array}{l} 1-d_j\gamma\epsilon+O(\epsilon^2),&i=j,\\ \gamma\epsilon+O(\epsilon^2),&i\not=j. \end{array} \right. \]

引入生成矩阵$H=(h_{ij})_{n\times n}$

\[ h_{ij}=\left\{ \begin{array}{l} d_j\gamma,&i=j,\\ -\gamma,&i\not=j\ \land\ \langle x_i,x_j\rangle\in E,\\ 0,&i\not=j\ \land\ \langle x_i,x_j\rangle\not\in E. \end{array} \right. \]

由 Markov 链的独立性，有

\[ m_{ij}(t+\epsilon)=\sum_km_{ik}(t)m_{kj}(\epsilon) \]

等式右边提出$k=j$项，得

\[ m_{ij}(t+\epsilon)=m_{ij}(t)m_{jj}(\epsilon)+\sum_{k\not=j}m_{ik}(t)m_{kj}(\epsilon) \]

带入生成矩阵

\[ m_{ij}(t+\epsilon)=m_{ij}(t)(1-\epsilon h_{jj})+\epsilon\sum_{k\not=j}m_{ik}(t)h_{kj} \]

移项，$\epsilon\to0$得

\[ \dfrac{\text dm_{ij}(t)}{\text dt}=-\sum_kh_{kj}m_{ik}(t) \]

$t=0$时不发生转移，故初始条件为$m_{ij}(0)=\delta_{ij}$.

解微分方程得$M(t)=e^{-Ht}$. 可得$\vec p(t)=M(t)\vec p(0)$.

推论： $$ \dfrac{\text dp_{i}(t)}{\text dt}=-\sum_kh_{ki}p_{k}(t) $$

CTQW¶

量子化：

概率向量 $\to$ 状态向量
转移矩阵 $\to$ 酉矩阵：由于$M(t)=e^{Ht}$非酉，取$U(t)=e^{-iHt}$

则$\ket{\psi(t)}=U(t)\ket{\psi(0)},\ p_k=|\langle k\ket{\psi(t)}|^2=|\bra kU(t)\ket{\psi(0)}|^2$.

下以线上CTQW为例，此时

\[ h_{ij}=\left\{ \begin{array}{l} 2\gamma,&i=j,\\ -\gamma,&i\not=j\ \land\ \langle x_i,x_j\rangle\in E,\\ 0,&i\not=j\ \land\ \langle x_i,x_j\rangle\not\in E. \end{array} \right. \]

故$H\ket{n}=-\gamma\ket{n-1}+2\gamma\ket{n}-\gamma\ket{n+1}$.

取$\gamma=(2\sqrt2)^{-1},\ket{\psi(0)}=\ket0$，概率分布如下

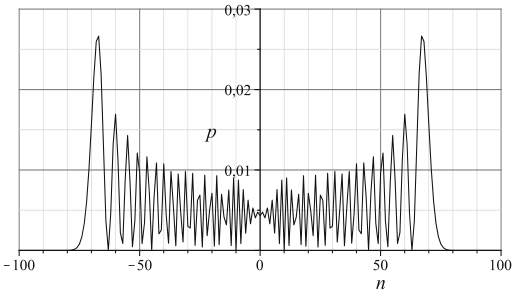
性质：

具有两个主要峰值，原点附近概率较低
$\gamma$为缩放因子，不改变形状
对称，$\langle n\rangle=0$
标准差$\sigma(t)\approx0.5t\propto t$

$U(t)=e^{-iHt}$，将$U(t)$展开为关于$H$的幂级数形式

$\ket{\psi(t)}=\sum\limits_{n=-\infty}^\infty e^{\frac{\pi i}{2}|n|-2i\gamma t}J_{|n|}(2\gamma t)\ket n$，其中$J$为第一类Bessel函数

$p(t,n)=|J_{|n|}(2\gamma t)|^2$

使用hiperwalk进行模拟：

import hiperwalk as hpw
import numpy as np

N = 201
line = hpw.Line(N)
qw = hpw.ContinuousTime(graph=line, gamma=1 / (2 * np.sqrt(2))) # 建立CTQW模型
vertex = N // 2
initial_state = qw.ket(vertex) # 游走者位置

final_state = qw.simulate(time=(N // 2, 1), initial_state=initial_state)
probability = qw.probability_distribution(final_state)
hpw.plot_probability_distribution(probability, animate=True, plot='line', rescale=True)