Finite-State Machines

组成：

1. 保存当前态的寄存器
2. 由输入和当前态计算下一状态的组合电路
3. 计算输出的组合电路

Info

自动机表达能力

理论上任何含寄存器(内存)的逻辑电路都可表为自动机

问题：表为一个自动机不切实际

• 解决：表为多个小自动机，通过自动机间通信组合成大自动机

基础自动机

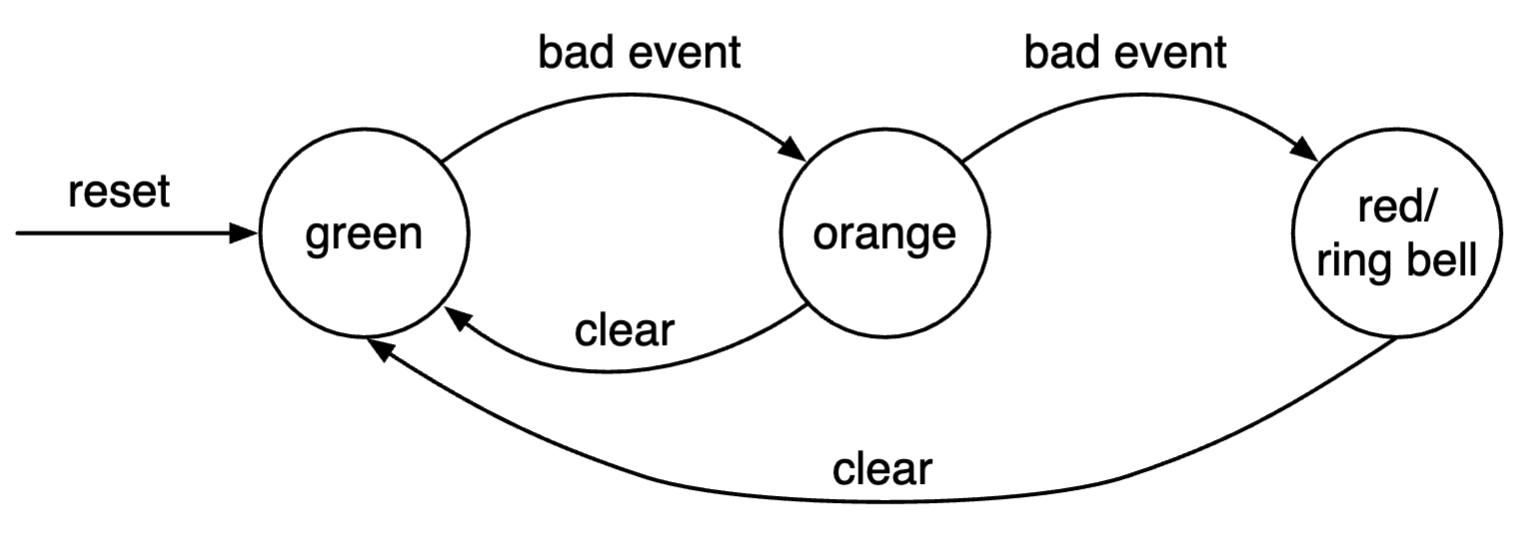
import chisel3._
import chisel3.util._

class SimpleFem extends Module {
    val io = IO(new Bundle{
        val badEvent = Input(Bool())
        val clear = Input(Bool())
        val ringBell = Output(Bool())
    })

    // 状态定义
    object State extends ChiselEnum {
        val green, orange, red = Value
    }
    import State._

    val stateReg = RegInit(green)

    // 状态转移
    switch (stateReg) {
        is (green) {
            when (io.badEvent) {
                stateReg := orange
            }
        }
        is (orange) {
            when (io.badEvent) {
                stateReg := red
            } .elsewhen (io.clear) {
                stateReg := green
            }
        }
        is (red) {
            when (io.clear) {
                stateReg := green
            }
        }
    }

    // 输出
    io.ringBell := stateReg === red
}

• 使用import State._简化状态表示

Note

Mealy VS Moore

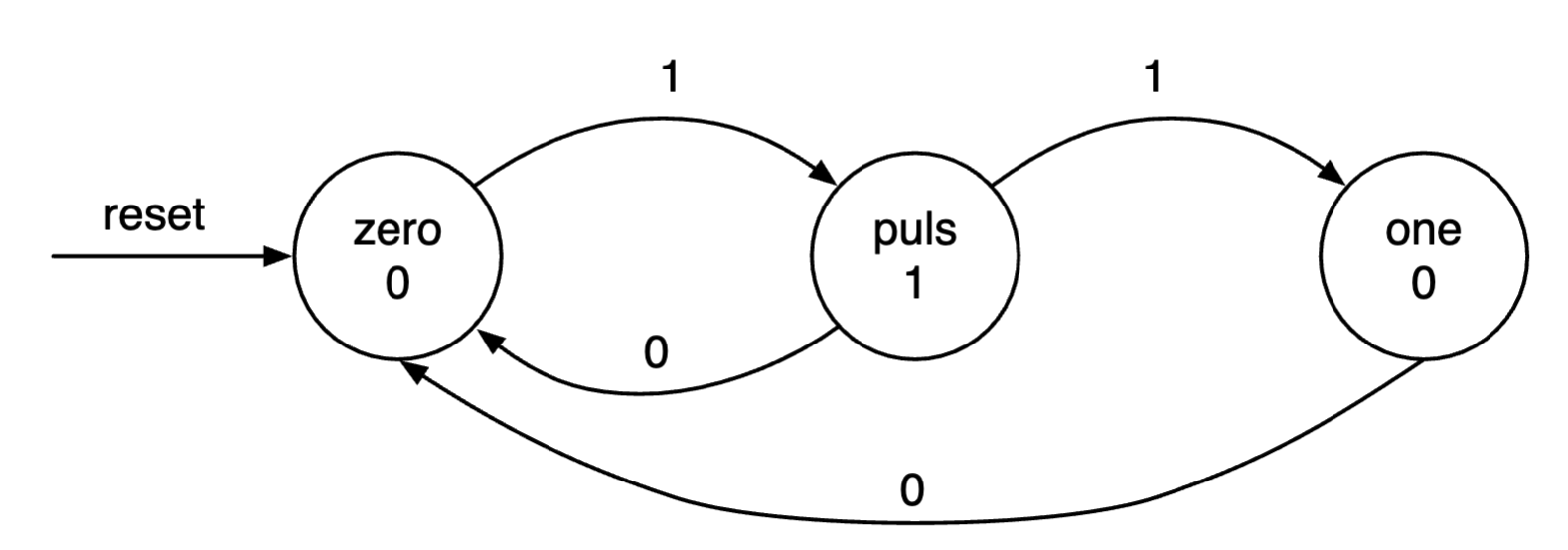
Moore：输出不依赖于输入，只依赖于状态

• 输出标在圆圈里

Mealy: 输出依赖于输入

• 输出标在箭头上

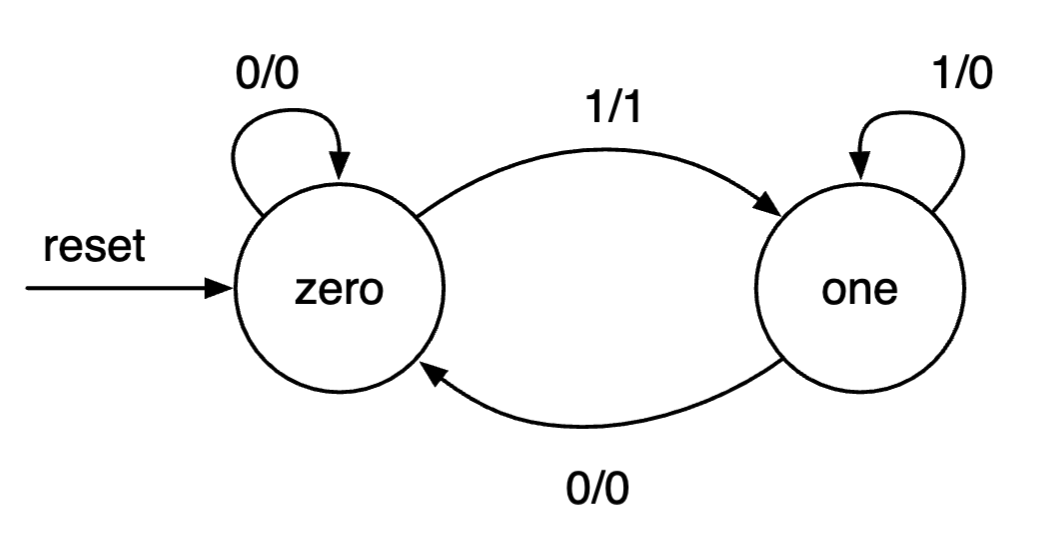
import chisel3._
import chisel3.util._

class RisingFsm extends Module {
    val io = IO(new Bundle {
        val din = Input(Bool())
        val risingEdge = Output(Bool())
    })

    object State extends ChiselEnum {
        val zero, one = Value
    }
    import State._

    val stateReg = RegInit(zero)
    io.risingEdge := false.B

    switch (stateReg) {
        is (zero) {
            when (io.din) {
                stateReg := one
                io.risingEdge := true.B
            }
        }
        is (one) {
            when (!io.din) {
                stateReg := zero
            }
        }
    }
}

• 输出设置在状态转移中

Important

自动机使用情景

在大于等于3个状态时使用自动机

上述上升沿检测电路可简化为一行：

val risingEdge = din & !RegNext(din)

生成结果：

// 自动机版本
module RisingFsm(
  input  clock,
         reset,
         io_din,
  output io_risingEdge
);

  reg stateReg;
  always @(posedge clock) begin
    if (reset)
      stateReg <= 1'h0;
    else if (stateReg)
      stateReg <= ~(stateReg & ~io_din) & stateReg;
    else
      stateReg <= io_din | stateReg;
  end // always @(posedge)
  assign io_risingEdge = ~stateReg & io_din;
endmodule

// 一行版本
module RisingFsm(
  input  clock,
         reset,
         io_din,
  output io_risingEdge
);

  reg io_risingEdge_REG;
  always @(posedge clock)
    io_risingEdge_REG <= io_din;
  assign io_risingEdge = io_din & ~io_risingEdge_REG;
endmodule

Mealy VS Moore

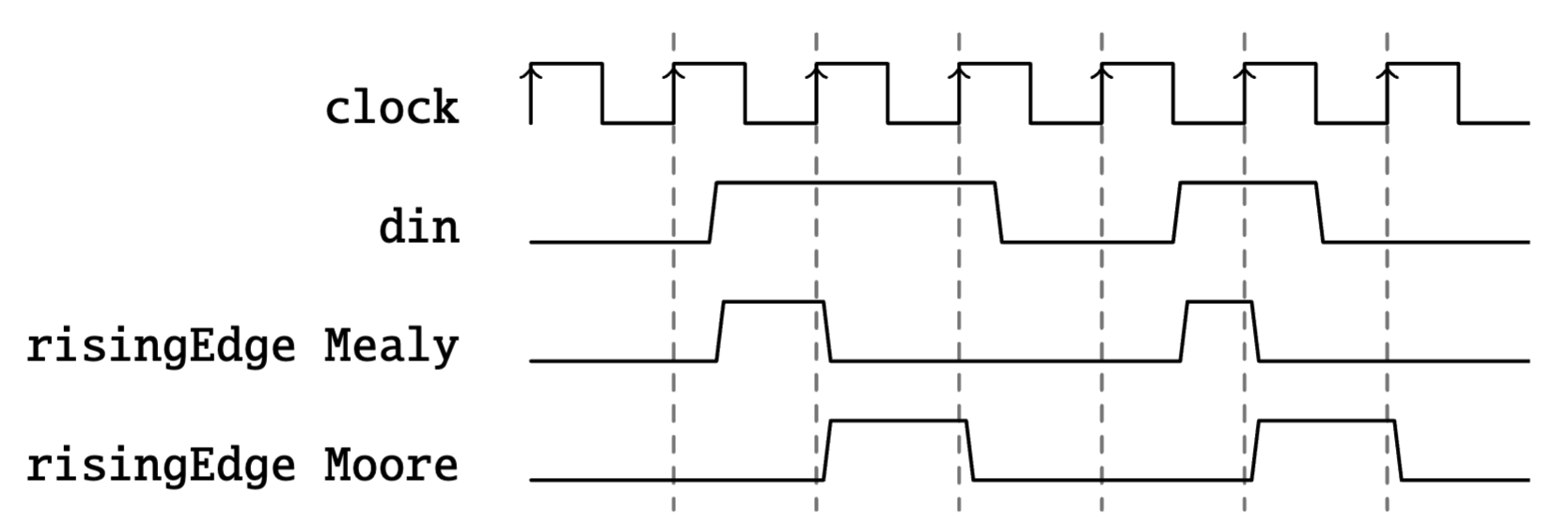
对于上升沿检测任务 Mealy自动机： Moore自动机： 波形： 对比：

• Mealy自动机需要的态更少，响应更快
• Mealy自动机输出小于一周期，而Moore输出为一周期
• Mealy自动机组合电路更复杂，多个自动机组合时将产生大延迟，难同步
• Moore更鲁棒，适用于自动机间的通信
• Mealy适用于小电路，且要求反应必须在同一周期