C++ STL¶
容器¶
共同背景¶
性质:所有的容器都可以视作一个前闭后开的结构
方法
| 方法 | 描述 | 示例 | 时间复杂度 |
|---|---|---|---|
| size | 返回容器包含的元素个数 | a.size() | \(O(1)\) |
| empty | 返回容器是否为空 | a.empty() | \(O(1)\) |
| begin | 返回容器首迭代器 | a.begin() | \(O(1)\) |
| end\(^1\) | 返回容器尾迭代器 | a.end() | \(O(1)\) |
注\(^1\):\(*a.end()\)是越界访问(前闭后开)
迭代器
概念:\(STL\)容器的指针,可用\(*\)解引用
声明:
重载<运算符
实现:
struct rec {
int id, value;
};
bool operator<(const rec &a, const rec &b) { return a.value < b.value; }
注:内置的\(int,string\)等类型本身可以比较大小
vector¶
概念:变长数组
实现:倍增
当实际存储数据量达到当前最大长度时,向内存申请两倍大小内存并转移当前数据;当实际存储数据量小于等于当前最大长度的四分之一时,释放一半的空间
性质:
1.支持随机访问
2.不支持任意位置\(O(1)\)插入(一般应在末尾进行增删)
声明
方法
| 方法 | 描述 | 示例 | 时间复杂度 |
|---|---|---|---|
| [] | 随机访问\(vector\) | a[i] | \(O(1)\) |
| clear | 清空\(vector\) | a.clear() | \(O(n)\) |
| front | 返回\(vector\)第一个元素\((*a.begin()/a[0])\) | a.front() | \(O(1)\) |
| back | 返回\(vector\)最后一个元素\((*--a.end()/a[a.size()-1])\) | a.back() | \(O(1)\) |
| push_back | 把元素插入到\(vector\)的尾部 | a.push_back(x) | \(O(1)\) |
| pop_back | 删除\(vector\)的最后一个元素 | a.pop_back() | \(O(1)\) |
迭代器
类型:随机访问迭代器
操作:
1.\(it + n\):类似指针移动
2.\(it2 - it1\):类似指针相减,得到两个迭代器对应下标之间的距离
遍历
\(*a.begin()\)与\(a[0]\)作用相同
for (int i = 0; i < a.size(); i++)
cout << a[i] << endl;
for (vector<int>::iterator it = a.begin(); it != a.end(); it++)
cout << *it << endl;
例 vector存图
思路:
邻接表存图的核心在于将边按照起点进行分类,由于数组长度不可变,所以我们需要手动管理存储位置,利用\(head\)维护每一类边的起点,利用\(next\)维护每一类边存储时的相邻关系,这样起点+后继就构成了一个单向链表的结构,从而实现顺序访问。
而\(vector\)为可变长数组,这意味着我们不需要手动维护每一类边的逻辑结构和存储结构之间的关系,只需要索引到每一类边的类别,让\(vector\)来维护存储即可,如图:
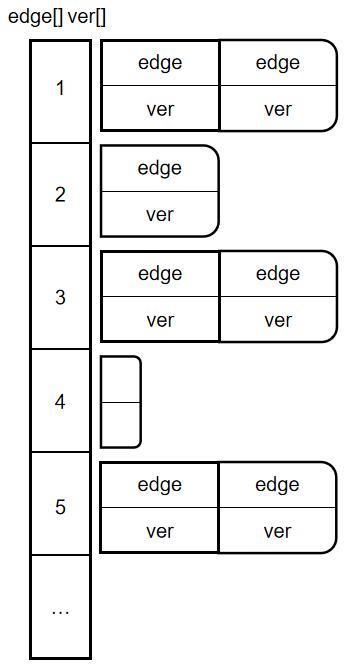
实现1:
vector<int> ver[N], edge[N];
void add(int x, int y, int z) {
ver[x].push_back(y); // 1.
edge[x].push_back(z);
}
for (int i = 0; i < ver[x].size(); i++) {
int y = ver[x][i], z = edge[x][i];
}
细节:
1.与链表实现的方式不同,链表实现中,由于\(head[]\)的存在,我们易于将后读入的边插入在链头;而\(vector\)适合在末尾进行元素的增删,利用\(pushback\)将后读入的边加到末尾即可
实现2:C++11
我们先考虑一下数据类(多字段数据)的存储。
我们有两种存储手段,第一是非常自然的表达出数据类的结构,最简单的方式是利用\(struct\);第二种是用多个数组分别维护这个数据类的各个字段。
再考虑索引手段,最自然的是运用指针对对象进行索引,但当我们使用数组时,与之匹配的一般是使用下标来索引。
对于数据类中的数值,可以直接将值存入数组中;对于数据类中的指针,我们按照指针的本质——地址,将我们用于索引对应元素的下标存入数组中。
现在我们需要访问该数据类的某个对象的某些属性。运用\(struct\)作为整体存储时,我们利用下标在数组中索引到目标对象,再直接访问它的属性,即下标\(\rightarrow\)对象\(\rightarrow\)属性;运用多个数组存储时,我们利用下标直接找到目标对象的某个属性,即下标\(\rightarrow\)属性\(_1\),下标\(\rightarrow\)属性\(_2\).
所以在邻接表存图和上述存图方法中,我们将边这一数据类的多个属性拆散到多个数组中,拿着索引直接到对应的数组中换取对应的属性;事实上,我们可以将他们以数据类的形态直接存入\(vector\)中,利用C++11的特性更加方便的存图读图。而数据类最简易的实现方式是存入\(pair\)中。
vector<pair<int, int>> edge[N]; // first: ver, second: edge; C++11不会将>>错判为右移
void add(int x, int y, int z) { edge[x].push_back(make_pair(y, z)); }
for (pair<int, int> i : edge[x]) { // 增强for循环
int y = i.first, z = i.second;
}
queue/priority_queue¶
声明
#include <queue>
struct rec{};
queue<rec> q;
priority_queue<int> q;
priority_queue<pair<int, int>> q;
注:\(pair\)比较大小时,以\(first\)为第一关键字,\(second\)为第二关键字;可用\(make\_pair(first,second)\)创建\(pair\)
queue
本质:循环队列
方法
| 方法 | 描述 | 示例 | 时间复杂度 |
|---|---|---|---|
| push | 从队尾入队 | q.push(x) | \(O(1)\) |
| pop | 从队头出队 | q.pop() | \(O(1)\) |
| front | 返回队头元素 | int x = q.front() | \(O(1)\) |
| back | 返回队尾元素 | int x = q.back() | \(O(1)\) |
priority_queue
本质:大根堆
方法
| 方法 | 描述 | 示例 | 时间复杂度 |
|---|---|---|---|
| push | 把元素插入堆 | q.push(x) | \(O(\log n)\) |
| pop | 删除堆顶元素 | q.pop() | \(O(\log n)\) |
| top | 返回堆顶元素(\(max\)) | int x = q.top() | \(O(1)\) |
例1 小根堆
思路1:用\(priority\_queue\)维护插入元素的相反数,取出后再取相反数还原
思路2:自定义结构体,重载小于号
例2 删除任意元素
思路:懒惰删除法
由于\(priority\_queue\)不支持任意位置删除,我们在优先队列外为被删除元素打上延迟标记。这样,在每次取最值操作时,利用延迟标记判断是否已删除,若已删除,则删除该堆顶元素并重取堆顶,直到取出的堆顶不带延迟标记为止,即为我们想要的堆顶元素。
deque¶
概念:支持在两端高效插入或删除元素的连续线性存储空间
性质:
1.能在头尾\(O(1)\)增删元素(类似\(queue\))
2.支持随机访问(类似\(vector\))
声明
方法
| 方法 | 描述 | 示例 | 时间复杂度 |
|---|---|---|---|
| [] | 随机访问\(deque\) | q[i] | \(O(1)\) |
| front | 返回队头元素 | int x = q.front() | \(O(1)\) |
| back | 返回队尾元素 | int x = q.back() | \(O(1)\) |
| push_back | 从队尾入队 | q.push_back(x) | \(O(1)\) |
| push_front | 从队头入队 | q.push_front(x) | \(O(1)\) |
| pop_back | 从队尾出队 | q.pop_back() | \(O(1)\) |
| pop_front | 从队头出队 | q.pop_front() | \(O(1)\) |
| clear | 清空\(deque\) | q.clear() | \(O(n)\) |
set/multiset¶
概念:有序(多重)集合
实现:红黑树
性质:
1.\(set\)不能有重复元素,\(multiset\)可以有重复元素
2.可维护集合的有序性
声明
方法
| 方法 | 描述 | 示例 | 时间复杂度 |
|---|---|---|---|
| clear | 清空集合 | s.clear() | |
| insert | 将元素插入集合中\(^1\) | s.insert(x) | \(O(\log n)\) |
| find | 返回等于\(x\)的元素的迭代器或\(s.end()\) | it = s.find(x) | \(O(\log n)\) |
| lower_bound | 返回\(\geqslant x\)的最小元素的迭代器或\(s.end()\) | it = s.lower_bound(x) | \(O(\log n)\) |
| upper_bound | 返回\(>x\)的最小元素的迭代器或\(s.end()\) | it = s.upper_bound(x) | \(O(\log n)\) |
| erase\(^2\) | 从集合中删除迭代器指向的元素并返回被删元素下一个的迭代器或\(s.end()\) | s.erase(it) | \(O(\log n)\) |
| 从集合中删除所有等于\(x\)的元素并返回成功删除的元素个数\(k\) | s.erase(x) | \(O(k+\log n)\) | |
| count | 返回集合中等于\(x\)的元素个数\(k\) | s.count(x) | \(O(k+\log n)\) |
注\(^1\):在\(set\)中,若元素已存在,则不会重复插入
注\(^2\):从\(multiset\)中删除一个等于\(x\)的元素(当不存在这类元素时不删除):
迭代器
类型:双向访问迭代器
操作:
\(++/--\):找到在排名上下一个/上一个元素(\(O(logn)\))
注:执行操作前后需进行检查,避免迭代器指向的位置超出首尾迭代器之间的范围
map¶
概念:键值对\(key\mapsto value\)的映射
实现:以\(key\)为关键码的红黑树
声明
#include <map>
// map<key_type, value_type> name;
map<long long, bool> vis; // 用做vis数组
map<string, int> hash; // 用作hash表
注:\(key\)需定义<运算符
方法
| 方法 | 描述 | 示例 | 时间复杂度 |
|---|---|---|---|
| clear | 清空\(map\) | h.clear() | \(O(n)\) |
| insert | 将键值对插入\(map\) | h.insert(make_pair(key, value)) | \(O(\log n)\) |
| erase | 删除\(map\)中的该键值对 | h.erase(make_pair(key, value)) | \(O(\log n)\) |
| 从\(map\)中删除迭代器指向的键值对 | h.erase(it) | \(O(\log n)\) | |
| find | 返回\(key\)为\(x\)的二元组\(pair\)<\(x, value\)>的迭代器或\(h.end()\) | it = h.find(x) | \(O(\log n)\) |
| []\(^1\) | 返回\(key\)映射到的\(value\)的引用 | value = h[key]; h[key] = value; | \(O(\log n)\) |
注\(^1\):若查找的\(key\)不存在,执行\(h[key]\)后会自动新建\((key,\theta)\)(其中\(\theta\)为广义零值),并返回对\(\theta\)的引用;时间一长会导致\(h\)中包含很多无用的零值二元组。故使用\([]\)进行查找前最好用\(find\)检查\(key\)是否存在。
迭代器
类型:双向访问迭代器
注:解引用后得到二元组\(pair\)<\(key, value\)>
例 给定\(n\)个字符串,\(m\)个问题,询问一个字符串出现的次数。
思路:将给定的字符串丢入\(map\)<\(string,int\)>中,并使用\([]\)获取出现次数。
实现:
map<string, int> h;
string s;
int main() {
for (int i = 0; i < n; i++) {
cin >> s;
h[s]++;
}
for (int i = 0; i < m; i++) {
cin >> s;
if (h.find(s) == h.end())
puts("0"); // puts自动换行
else
cout << h[s] << endl;
}
}
bitset¶
概念:多位二进制数(状压二进制数组)
声明
方法
下记位数为\(n\).
在估算程序运行时间时,一般以32位整数的运算次数为基准,因此\(n\)位\(bitset\)执行一次位运算复杂度可视为\(\dfrac{1}{32}*n=\dfrac{n}{32}\),效率较高
| 方法 | 描述 | 示例 |
|---|---|---|
| ~ | 返回\(bitset\)按位取反的结果 | s = ~s |
| &,|,^ | 返回对两个位数相同的\(bitset\)按位与、或、异或的结果 | s = s1&s2 |
| &=,|=,^= | 同上,相当于s = s & s1 | s &= s1 |
| >>,<< | 返回把一个\(bitset\)右移、左移\(^1\)若干位的结果 | s = s1 << k |
| >>=,<<= | 同上,相当于s = s << k | s <<= k |
| ==,!= | 比较两个位数相同的\(bitset\)代表的二进制数是否相等 | s1 == s2 |
| [] | 返回对\(bitset\)第\(k\)位\(^2\)的引用 | s[k] = 0;x = s[k]; |
| count | 返回\(bitset\)有多少位为1 | s.count() |
| any | 返回\(bitset\)是否至少有一位为1 | s.any() |
| none | 返回\(bitset\)是否所有位为0 | s.none() |
| set | 把\(bitset\)所有位变为1 | s.set() |
| 把\(bitset\)第\(k\)位改为\(x\)\((s[k]=x)\) | s.set(k, x) | |
| reset | 把\(bitset\)所有位变为0 | s.reset() |
| 把\(bitset\)第\(k\)位改为0\((s[k]=0)\) | s.reset(k) | |
| flip | 把\(bitset\)所有位取反\((s=\sim s)\) | s.flip() |
| 把\(bitset\)第\(k\)位取反\((s[k]\)^=\(1)\) | s.flip(k) |
注\(^1\):高位自然溢出
注\(^2\):最低位为第\(0\)位,最高位为第\(n-1\)位
算法¶
以下函数作用在序列上,接受两个迭代器或指针\(l,r\),对下标\(\in[l,r)\)的元素执行一系列操作。
reverse 翻转¶
unique 去重¶
返回去重之后的未尾元素下一个位置的迭代器或指针,利用指针减法可计算出去重后元素个数m.
int m = unique(a.begin(), a.end()) - a.begin(); // vector去重
int m = unique(a + 1, a + n + 1) - (a + 1); // 数组去重
注:去重前需进行排序
random_shuffle 随机打乱¶
next_permutation/pre_permutation 下/上一个排列¶
将两个迭代器或指针指定的部分看作一个排列,将其更新为在这些元素构成的全排列中,字典序排在下/上一个的排列;若不存在排名更靠后/前的排列,则返回\(false\),否则返回\(true\).
例 按字典序输出\(1..n\)的全排列。
for (int i = 1; i <= n; i++) a[i] = i;
do {
for (int i = 1; i <= n; i++)
cout << a[i] << ' ';
cout << endl;
} while (next_premutation(a + 1, a + n + 1));
sort 快速排序¶
对两个迭代器或指针指定的部分进行快速排序,可传入定义大小比较的函数或重载<运算符。
int a[N];
bool cmp(int a, int b) { return a > b; } // true不交换,false交换,故为降序
sort(a + 1, a + 1 + n, cmp);
struct rec {
int x, int y;
};
bool operator<(const rec &a, const rec &b) {
return a.x < b.x || a.x == b.x && a.y < b.y;
}
vector<rec> a;
sort(a.begin(), a.end());
lower_bound/upper_bound 二分查找¶
\(lower\_bound\)返回指向第一个\(\geqslant x\)的元素的迭代器或指针,\(upper\_bound\)返回指向第一个\(>x\)的元素的迭代器或指针,查找失败返回尾迭代器。
注:查找前需进行排序