链表与邻接表¶
链表¶
双向链表
定义:支持在任意位置插入或删除,但只能按顺序依次访问其中的元素的数据结构
性质:
1.支持在任意位置插入、删除元素
2.只能按顺序访问其中的元素
存储:
用\(struct\)表示节点,用\(prev\)和\(next\)指向前后相邻的两个节点;建立额外的两个节点\(head\)与\(tail\)代表链表头尾,避免左右两端或空链表访问越界,如图:
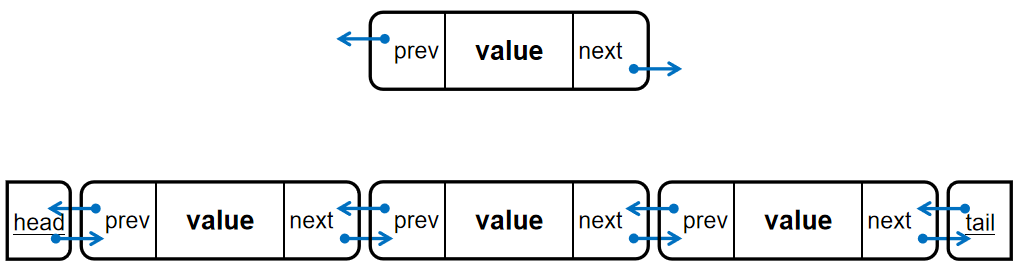
操作:
1.建表\(initialize()\):
初始化\(head\)与\(tail\);此时数组中已有两个元素,故\(tot\)更新为2,如图:
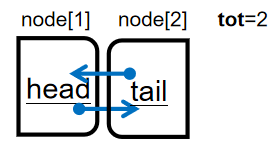
2.插入元素\(insert(p,val)\):
为了在节点\(p\)后插入新节点,我们先新建节点\(q\),并完成值的写入;接着我们从后往前处理连接关系:先是\(p\)->\(next\),从插入后的结果来看,影响的是\(p\)->\(next\)的\(prev\),再看\(q\),我们直接将它的\(prev\)与\(next\)连接完成,最后是\(p\),从插入后的结果来看,影响的是\(p\)的\(next\),如图:
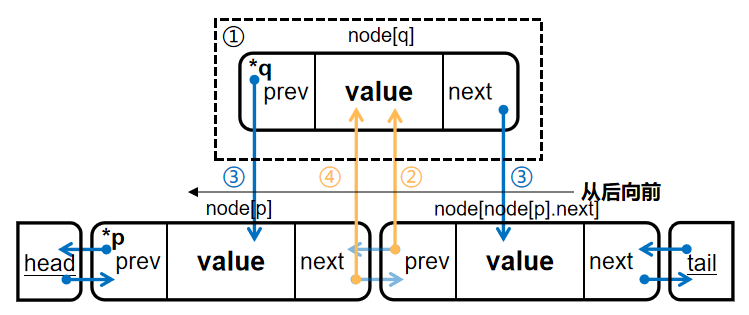
至于为何按照从后往前的顺序,因为我们在节点\(p\)后插入节点,新节点会成为\(p\)->\(next\),为了防止丢失\(p\)->\(next\)的索引,故须按从后往前的顺序进行处理。
3.删除元素\(remove(p)\):
删除节点\(p\)会影响\(p\)->\(next\)的\(prev\)和\(p\)->\(prev\)的\(next\),直接修改即可,如图:

若为指针存储,可以将\(p\)直接\(delete\)释放内存;若为数组模拟,无法删除,直接无视即可。
4.删表\(recycle()/clear()\):
对于指针存储,从\(head\)->\(next\)开始依次删去\(prev\),并利用\(next\)向后移动\(head\)遍历链表,最后将\(tail\)删去,如图:

对于数组模拟,只需\(memset\) \(node[]\)并置\(head,tail,tot\)为0即可。
实现1:指针
struct Node {
int value;
Node *prev, *next;
};
Node *head, *tail; // *head, *tail仅为指针,并未指向具体的对象
void initialize() {
head = new Node();
tail = new Node();
head->next = tail;
tail->prev = head;
}
void insert(Node *p, int val) {
Node *q = new Node(); // 1.创建新对象 2. 用指针指向新对象
q->value = val;
p->next->prev = q;
q->next = p->next;
q->prev = p;
p->next = q;
}
void remove(Node *p) {
p->prev->next = p->next;
p->next->prev = p->prev;
delete p;
}
void recycle() {
while (head != tail) {
head = head->next;
delete head->prev;
}
delete tail;
}
实现2:数组
struct Node {
int value;
int prev, next;
} node[N];
int head, tail, tot;
int initialize() {
tot = 2;
head = 1, tail = 2;
node[head].next = tail;
node[tail].prev = head;
}
int insert(int p, int val) {
int q = ++tot;
node[q].value = val;
node[node[p].next].prev = q; // 下标本身无prev,next,需从node[]中取出对应元素来访问prev,next
node[q].next = node[p].next; // prev,next存储的是下标,赋值时需注意类型匹配
node[q].prev = p;
node[p].next = q;
}
void remove(int p) {
node[node[p].prev].next = node[p].next;
node[node[p].next].prev = node[p].prev;
}
void clear() {
memset(node, 0, sizeof(node));
head = tail = tot = 0;
}
| 随机访问 | 任意位置插入删除 | |
|---|---|---|
| 数组 | √ | × |
| 链表 | × | √ |
例1邻值查找
思路1:链表
由于\(1\leqslant j<i\),所以\(a\)自然划分为\(a[1..i),a[i]\)和\(a[i+1,n]\),且\(a[i+1,n]\)对\(a_j\)的寻找没有影响。
根据这样的思路,我们在考虑\(a_n\)的邻值时,可以在\(a[1..n)\)中查找;在考虑\(a_{n-1}\)的邻值时,需要排除\(a_n\)的影响,只能在\(a[1..n-1)\)中查找。
同时,我们希望\(\{a_n\}\)已经有序,并能知道\(a_i\)邻值的原始下标。为此,我们可以采取双关键字排序,利用\(pair\)将\(a_i\)的值写入\(first\),将原始下标\(i\)写入\(second\),并对\(first\)关键字进行排序。这样我们就能方便的找到\(a_i\)的邻值了。
并且排序有一个非常好的性质,如果我们删除已有序序列中的任意元素,剩下的元素仍然是有序的。结合上述分析,我们从\(a_n\)开始寻找邻值,寻找完毕后,将\(a_n\)删除,再寻找\(a_{n-1}\)的邻值,以此类推。
但是问题随即出现:在对存有\(a_i\)值和原始下标的\(pair\)<\(int,int\)>\([]\)进行排序后,原先的\(a_n\)未必处于最后方,\(a_{n-1}\)也未必与\(a_n\)相邻。而数组是不支持在任意位置插入删除元素的数据结构,所以我们需要将这两个字段的数据\((a_i的值,原始下标)\)交给能支持任意位置插入删除的链表进行维护。
同时我们注意到链表仅支持顺序访问,这对寻找邻值没有影响,因为在排好序的\(pair\)<\(int,int\)>\([]\)中,\(p\)的邻值一定在\(p\)->\(prev\)和\(p\)->\(next\)之间,符合顺序访问的要求。但是我们在寻找邻值时按照\(a_n..a_2\)的顺序进行,但原始下标为\(i\)和\(i-1\)的数据未必在链表上也连续,所以我们希望借助数组\(b\)按照原始下标的顺序将对链表块的索引进行存储,以实现数组下标到链表位置的转换,即链表的跳跃式访问。
总结一下,我们需要做如下操作:
1.将原始数据\((a_i,i)\)存储到\(pair\)<\(int,int\)>\([]\)中并按\(first\)关键字排序
2.将排序后的数据存储到链表上,并使用\(*b[i]\)指向原始下标为\(i\)的\(a_i\)所在的链表块
3.从原始下标为\(n\)开始寻找邻值,找到后暂存答案,并将该元素对应的链表块删除,继续寻找前一个元素的邻值;最后输出答案
实现:
pair<int, int> p[N], ans[N];
struct Node {
int value, pos;
Node *prev, *next;
};
Node *head, *tail;
Node *b[N];
void initialize() {
head = new Node();
tail = new Node();
head->next = tail;
tail->prev = head;
}
Node *insert(Node *p, int val, int pos) { // 返回指向新块的指针
Node *q = new Node();
q->value = val;
q->pos = pos;
p->next->prev = q;
q->next = p->next;
q->prev = p;
p->next = q;
return q;
}
void remove(Node *p) {
p->next->prev = p->prev;
p->prev->next = p->next;
delete p;
} // 无需回收,循环的同时在删除链表
int main() {
int n, pre, nxt;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> p[i].first;
p[i].second = i;
}
sort(p, p + n); // pair默认以first为第一关键字升序排列
initialize();
for (int i = 0; i < n; i++)
if (!i)
b[p[i].second] = insert(head, p[i].first, p[i].second);
else
b[p[i].second] = insert(b[p[i - 1].second], p[i].first, p[i].second);
for (int i = n - 1; i > 0; i--) {
if (b[i]->next == tail)
ans[i].first = b[i]->value - b[i]->prev->value,
ans[i].second = b[i]->prev->pos;
else if (b[i]->prev == head)
ans[i].first = b[i]->next->value - b[i]->value,
ans[i].second = b[i]->next->pos;
else {
pre = abs(b[i]->prev->value - b[i]->value),
nxt = abs(b[i]->next->value - b[i]->value);
if (pre < nxt)
ans[i].first = pre, ans[i].second = b[i]->prev->pos;
else if (nxt < pre)
ans[i].first = nxt, ans[i].second = b[i]->next->pos;
else {
ans[i].first = pre;
ans[i].second = b[i]->prev->pos; // 前驱小于后继
}
}
remove(b[i]);
}
for (int i = 1; i < n; i++)
cout << ans[i].first << ' ' << ans[i].second + 1 << endl; // 存储时从0开始,题目下标从1开始
return 0;
}
思路2:STL set
仿照以上思路,对称地考虑,我们可以将元素一个一个插入来消除后面元素对目前已有元素的干扰。这样,我们希望有这样一个数据结构,可以维护一个有序集合\(S\),且支持动态插入与前驱后继查询。而STL set为我们实现了一个二叉平衡树可以满足我们的要求。
实现:
struct rec {
int id, value;
} cur;
bool operator<(const rec &a, const rec &b) { return a.value < b.value; }
set<rec> s;
int main() {
int n, a;
set<rec>::iterator pre, nxt;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a;
cur.id = i + 1, cur.value = a;
if (i) {
pre = --s.lower_bound(cur); // 1.
nxt = s.upper_bound(cur);
if (pre == s.end())
cout << abs(a - nxt->value) << ' ' << nxt->id << endl;
else if (nxt == s.end())
cout << abs(a - pre->value) << ' ' << pre->id << endl;
else {
if (abs(a - pre->value) < abs(a - nxt->value))
cout << abs(a - pre->value) << ' ' << pre->id << endl;
else if (abs(a - pre->value) > abs(a - nxt->value))
cout << abs(a - nxt->value) << ' ' << nxt->id << endl;
else
cout << abs(a - pre->value) << ' ' << pre->id << endl;
}
}
s.insert(cur);
}
return 0;
}
细节:
1.\(set.lower\_bound(x)\)会返回\(set\)中第一个\(\geqslant x\)的元素,\(set.upper\_bound(x)\)会返回\(set\)中第一个\(> x\)的元素;因此,\(set.lower\_bound(x)\)的前一个元素即为\(x\)的前驱,即\(<x\)的最后一个元素,而\(set.upper\_bound(x)\)即为\(x\)的后继。
值得注意的是,--需写在函数调用前,否则含义变为将返回值递减,但返回递减前的值(a--返回a,副作用使得a-=1)。
邻接表¶
定义:带有索引(表头)数组的多个数据链表构成的结构集合
性质:
1.数据被分成若干类,每一类数据构成一个链表
2.可通过表头数组定位到某一类数据对应的链表
存储:
\(head\)存储当前类别的表头,每个元素的\(next\)指向下一个链表块,末端的链表块指向\(0\)值,如图:
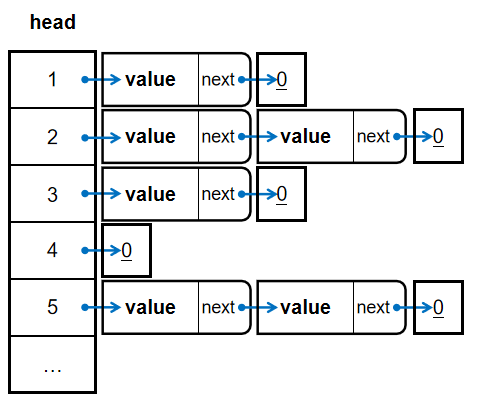
应用:用于树、图的存储
将图的每条边按起点分类(易于按起点遍历),同时按顺序存储权值\(edge[]\)与终点\(ver[]\),而链表块的\(value\)存储对应边的数组下标,通过\(head,next\)指向后得到相应的\(value\),如图:
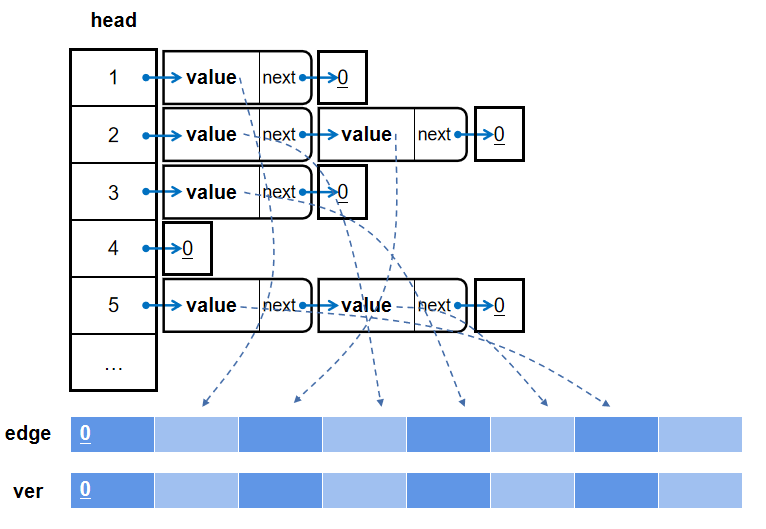
由于\(edge,ver,next\)是对每条边存的,我们可以将\(edge[i],ver[i],next[i]\)理解为\(Graph[i].edge,Graph[i].ver,Graph[i].next\),将下标放入对应字段的数组中实现属性的读取。
操作:
1.加边\(add(x,y,z)\):
即加入有向边\((x,y)\),权值为\(z\).
由于\(head\)可以定位到以某一边为起点的一类边,我们利用\(head[x]\)进行插入,如图:
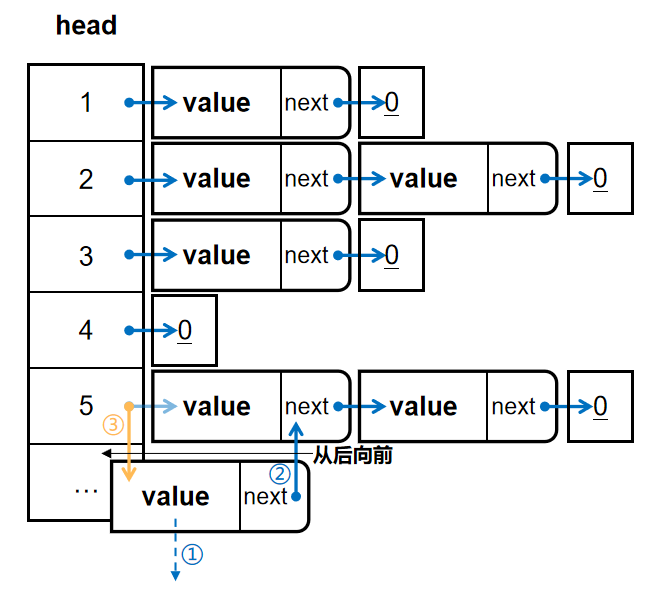
由于我们将新边插入到\(head[x]\)后,故需按照从后往前的顺序,在完成权值与终点的存储后,从新边\(next[tot]\)开始进行更新,防止丢失链表块\(head[x]\)的索引。从结果来看,链表块\(head[x]\)并没有发生改变,无需更新。
容易发现,后插入的边在链表上的位置会在先插入的边的前面;同时,不在链尾插入的原因是无法直接访问到链尾。
2.访问\(x\)的出边:
从\(head[x]\)开始,利用\(next\)依次向后访问,直到遇到\(0\)终止。注意\(head,next\)存储的是边的下标,\(head\)存储的是所有类别的边的最后一个存入的边的下标,而\(next\)存储的是当前边所处链表块的下一个链表块对应的边的下标。
实现:
void add(int x, int y, int z) {
ver[++tot] = y, edge[tot] = z; // 1.
nxt[tot] = head[x], head[x] = tot; // 2.
}
for (int i = head[x]; i; i = nxt[i]) {
int y = ver[i], z = edge[i];
}
细节:
1.使用++\(tot\),使边的下标从1开始存储,从而使得边的下标为\(0\)意味着终止;对于无向图,可以初始化\(tot=1\),从2开始存储,从而可以利用成对变换找到与之反向的边(如\(2\oplus1=3,3\oplus1=2\))
2.不命名为\(next[]\):防止重名