递推与递归¶
状态空间¶
定义:一个实际问题的各种可能情况构成的集合
程序的运行是对于状态空间的遍历。
算法和数据结构通过划分、归纳、提取、抽象来帮助提高状态空间遍历的效率。
效率提升的本质:不局限于数据本身,而关注数据的某些宏观性质,从另一维度遍历数据的关键性质
递推与递归的宏观描述¶
基本要素:
1.求解步骤相似性:将\(f(n)\)化为数据规模更小的\(f(n-1)\),或者将\(f(n-1)\)推至\(f(n)\),数据规模不同,求解方法一致
2.边界:边界是构成解的起点,亦是问题划分的终点,是问题求解的最小单位
递推¶
释义:递是传递,是不同问题规模之间的关系;推是求解方向,即由问题边界出发,正向推出问题的解。每次向规模更大的方向推出时,求解方法一致,从而单向遍历了整个状态空间
递归¶
释义:递是向下传递的动作,是将大数据规模的问题拆分成小数据规模的问题;而归是对小问题规模的解进行整合,从而获得大规模问题的解
由此看来,递归设计的要点在于对相似子问题的划分以及处理大小问题规模之间的关系。从关系处理的角度来看,递归的两步设计如下:
1.递:
(1)边界判断:递的前提是能递,需判断是否到达边界,进而决定是否继续向递;同时,到达边界意味着一个求解过程的结束,应进行最终结果的保存
注:此处的边界不同于基本要素中的边界。此处的边界指求解的终点,而基本要素中指求解的起点。递归的起点由初始调用传入。
(2)求解子问题:对当前问题规模进行划分,递归调用自身求解子问题。此处表达原问题与子问题之间递的关系(缩小、求解)
2.归:
(1)合并子问题:此时子问题已完成求解,应利用子问题的解组成原问题的解。此处表达子问题到原问题之间归的关系(扩展)
(2)返回上一级:目前问题是规模更大的问题的子问题,求解答案可由return返回,存在调用栈中的临时变量可自动释放,但全局变量并不会自动消除目前问题求解过程中带来的影响;因此,所谓回溯即是手动将全局变量调整至该问题求解前的状态,以正确结束该问题的求解,使得全局变量的状态与问题求解状态保持一致
由此,递归设计过程如下:
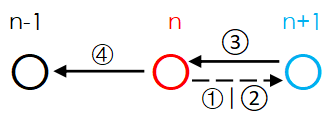
递归设计时,不应从递归实际的执行顺序考虑进行设计(树形),而应该抓住递归部分的本质:关系处理(线性),才能清楚地写出递归
递推与递归的简单应用¶
例1递归实现指数型枚举
思路1:二进制状压
由于每个数字只有选或不选两种状态,我们可以用一个二进制数来表示所有数字的选择状况。
时间复杂度估计:
共\(2^n\)种情况,每种情况输出用时\(O(n)\),故时间复杂度为\(O(n*2^n)\)
思路2:递归
边界:
起点:所有数字都不选
终点:决定好第n个数字选择状态
递归:
递:考虑下一数字,选或不选两种情况
归:此题为输出答案,故无需返回结果
实现:
void choose(int dep, int k) { // dep为目前要决定选择状态的数字,k为目前选择的数字个数
if (dep == n + 1) {
for (int i = 0; i < k; i++)
cout << chosen[i] << " ";
cout << endl;
return;
}
choose(dep + 1, k);
chosen[k] = dep;
choose(dep + 1, k + 1);
} // 1.
int main() {
cin >> n;
choose(1, 0);
return 0;
}
细节:
1.此处未回溯:理论上来说,由于涉及到了全局变量chosen[N],此处应进行相应的回溯操作,即chosen[k] = 0;但事实上,由于使用k来表示已选数字个数,我们只要保证chosen[0..k-1]中对应为我们选择的k个数字,而此递归中的k为局部变量,自动释放,chosen[k]同步失去意义,所以我们始终保证chosen[0..k-1]中数据符合实际情况;进一步地,当下一次使用到这个选择位时,将会自动覆盖原有数据。
碰到与固有思考模式不符的地方,可以从简化的角度进行考虑,即考虑在某种问题情境下,某些步骤是否必要
例2递归实现组合型枚举
思路:剪枝
与上一题 相比,此处的限制条件更为严格,要求选择个数为m个。为此,我们可以从以下两个角度考虑进行剪枝:
1.已选个数超过m个(过大) 2.将所有未选元素全部选中也无法达到m个(过小)
此处我们仅用到了选择个数的限制,所以仍然将达到选择范围边界做终点,实现如下:
void choose(int dep, int k) {
if (k > m || k + (n - dep + 1) < m)
return;
if (dep == n + 1) {
for (int i = 0; i < k; i++)
cout << chosen[i] << " ";
cout << endl;
return;
}
chosen[k] = dep;
choose(dep + 1, k + 1); // 要求按字典序递增排列,故尽量先进行选择,先得到的答案字典序靠前
choose(dep + 1, k);
}
或者,我们可以按照题目要求,将选择个数达到边界作为终点,同理,可以从两个角度进行剪枝:
1.超出选择范围 2.将所有未选元素全部选中也无法达到m个
实现如下:
void choose(int dep, int k) {
if (dep > n + 1 || k + n - dep + 1 < m)
return;
if (k == m) {
for (int i = 0; i < k; i++)
cout << chosen[i] << " ";
cout << endl;
return;
}
chosen[k] = dep;
choose(dep + 1, k + 1);
choose(dep + 1, k);
}
从代码简化的角度来看,两者等价。以第一种实现为例:
终点处的if-return暗含了
由于dep连续递增,故原if-return断绝了dep>n+1的可能性。
这样,可以认为该递归有3个剪枝条件:k>m,k+(n-dep+1)
同理,第二种实现暗含了k>m的条件。由此看来,二者剪枝条件等价,只是利用不同的终点省略了不同的剪枝条件。
进一步地,k+(n-dep+1)==m不能作为终点:因为dep,k递增,故k+(n-dep+1)单调性未知,会暗含错误的剪枝条件。
时间复杂度估计:
由于及时的剪枝,程序并不会枚举出不符合组合意义的状态,程序仅遍历了符合组合意义的状态空间\(O(C_n^m)\),算上每个状态输出用时,复杂度为\(O(m*C_n^m)\)
例3递归实现排列型枚举
思路:递归
边界:
起点:所有数字未选
终点:已选n个数字
递归:
递:选择所有未被选择的数字
归:此题为输出答案,故无需返回结果
标记数字是否被选择:使用visit数组,若vis[i]=0代表未选择,vis[i]=1代表已选择
实现:
void dfs(int dep) {
if (dep == n + 1) {
for (int i = 1; i <= n; i++)
cout << p[i] << " ";
cout << endl;
return;
}
for (int i = 1; i <= n; i++) // 1.
if (!vis[i]) {
p[dep] = i, vis[i] = 1;
dfs(dep + 1);
vis[i] = 0; // 2.
}
}
int main() {
cin >> n;
dfs(1);
return 0;
}
细节:
1.使用循环语句,配合if语句,考虑所有未选择数字
2.此处不写p[N]=0原因同上:p[N]意义由p本身和dep共同控制,dep自动变化,故无需考虑p[N];
此处vis[N]仅由本身取值表示意义,故需进行回溯,保证记录的访问状态与实际一致
例4费解的开关
思路1:递归
我们可以将点击过程视作异或操作,而异或属于按位操作,具有交换律,所以点击的顺序并不影响点击结果。进一步地,我们能得出任意一开关不会被重复点击,否则我们可以调整点击顺序使两次重复点击相邻,即相当于没有进行任何点击,不可能为最优解。
由此,我们可以将从25个点中选k个点(\(k\leqslant6\))设置为我们的状态空间,遍历时需进行\(6*C_{25}^6\)次运算和比较。
思路2:递推
上述思路运算量大的原因在于枚举地没有顺序;人为规定按行的顺序向下填,不难发现,在结束(固定)第n行的填写后(按行顺序,即前n行填写完成),仅第n+1行能对第n行的状态产生影响。具体表现为第n行若含有0,则第n+1行对应位置需进行一次开关操作,否则无法打开该位置的灯。
这样,一旦第1排的灯完成操作,按照行的顺序,后n-1排灯的操作也就唯一确定了。因此,只需枚举第1行的操作策略,按照行的顺序递推,即可求解,遍历时最多操作\(2^5*20\)次运算。
实现:
void op(int i, int j) {
curMap[i][j] ^= 1;
curMap[i - 1][j] ^= 1;
curMap[i][j - 1] ^= 1;
curMap[i + 1][j] ^= 1;
curMap[i][j + 1] ^= 1;
cnt++;
}
void resetMap() {
for (int i = 1; i <= 5; i++)
for (int j = 1; j <= 5; j++)
curMap[i][j] = Map[i][j];
}
int main() {
cin >> n;
for (int t = 0; t < n; t++) {
getchar(); // 1.
ans = INF; // 3.
for (int i = 1; i <= 5; i++) {
for (int j = 1; j <= 5; j++)
Map[i][j] = getchar() ^ 48; // 2.
getchar();
}
for (int S = 0; S < (1 << 5); S++) {
cnt = 0, resetMap(); // 3.
for (int i = 0; i < 5; i++)
if ((S >> i) & 1)
op(1, i + 1);
for (int i = 2; i <= 5; i++)
for (int j = 1; j <= 5; j++)
if (curMap[i - 1][j] == 0)
op(i, j);
bool flag = true;
for (int i = 1; i <= 5; i++)
flag &= curMap[5][i];
if (flag)
ans = min(ans, cnt);
}
cout << (ans > 6 ? -1 : ans) << endl;
}
return 0;
}
细节:
1.由于采用getchar()读取数据,需注意未被读入的回车:此处每组数据前都有回车需要作读入处理
2.getchar()读入数据为char类型,需将其转化为对应的数字。
理论上来说,读入字符\(c-n='0'-0=48\),即\(n=c-48=c-\overline{110000}_{(2)}\)
而对于数字范围的c取值为\(\overline{110000}_{(2)}\sim \overline{111001}_{(2)}\),减去\(\overline{110000}_{(2)}\)不会发生借位,而是将最高两位的1置为0。因此,我们可以考虑使用\(c\oplus \overline{110000}_{(2)}=c \oplus 48\)实现字符向数字的转化。
3.多测不清空,爆零两行泪
例4 Strange Towers of Hanoi
思路:递推
按照由特殊到一般的思路,我们先考虑盘数较少的情况,然后从中提取出一般规律。
当n=1时显然\(f_1=1\)
当n=2时显然\(f_2=3\)
当n=3时显然\(f_3=5\),图示如下:

事实上,我们可以将中间三步合并,即将下面两个盘子看作一个整体,图示如下:
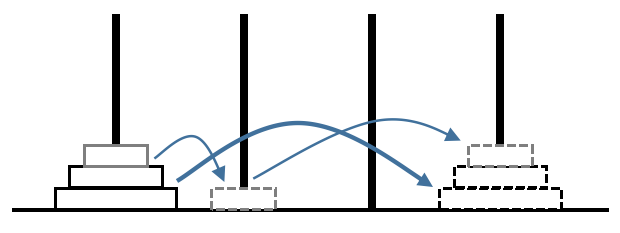
容易发现一般规律:先从左1塔中搬下一部分至左2塔,再将剩余部分搬至右1塔,最后将左2塔搬至右2塔。
当\(n\geqslant4\)时,图示如下:
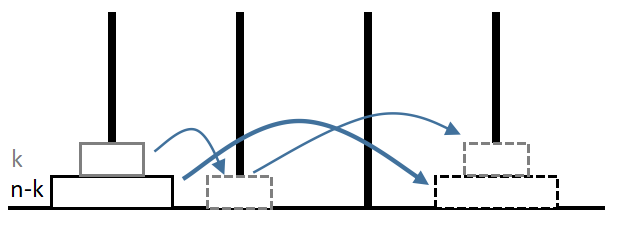
这样,我们只需要枚举所有的k,使\(f_n\)最小即可。
值得注意的是,在进行第一次操作时,由于剩余部分一定大于上部,故四根柱子都可用;进行第二次操作时,由于剩余部分一定大于暂时存放的上部,故暂存柱不可用,仅有三根柱子可用;进行第三次操作时,上部小于已归位的剩余部分,故四根柱子都可用;写作数学表达式即为:
\(f_n=\min\limits_{k}\{2f_k+d_{n-k}\}\)
因此,我们需要预处理出三根柱子可用的情形:
当n=1时显然\(d_1=1\)
当n=2时显然\(d_2=3\)
当n=3时显然\(d_3=7\),图示如下:
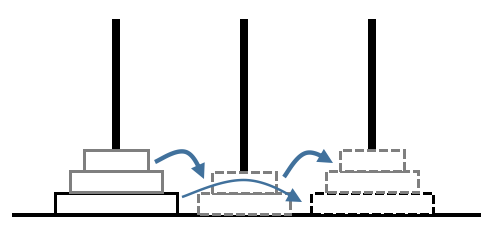
相当于我们将最上面两个盘子看作整体,即\(d_3=2d_2+1=7\)
当\(n\geqslant4\)时,图示如下:
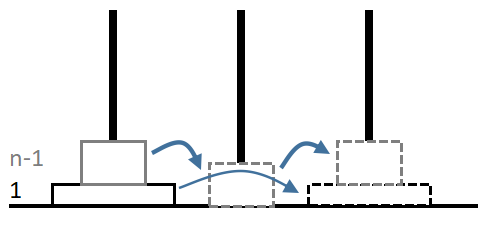
即\(d_n=2d_{n-1}+1\),这样我们就可以对\(d_n\)进行初始化。
这里体现的就是递推思想:大规模的问题从小规模问题处获得答案,即从小规模问题的答案推出大规模问题的答案。
实现:
memset(f, 0x3f, sizeof(f)); // 取min,需初始化为INF
d[1] = f[1] = 1;
for (int i = 2; i <= 12; i++)
d[i] = 2 * d[i - 1] + 1;
for (int i = 2; i <= 12; i++)
for (int j = 1; j < i; j++)
f[i] = min(f[i], 2 * f[j] + d[i - j]);
推广:
若为n盘m塔问题,都有
\(f(n,m)=\min\limits_k\{2*f(k,m)+f(n-k,m-1)\}\)
从等式右边到左边,m递增,故外层递增枚举m,并将n=3情形作为边界。
时间复杂度估计:
状态空间大小:\((m-2)*n\) 转移时间:\(O(n)\)
故时间复杂度为\(O(m*n^2)\)
分治¶
定义:把一个问题划分为若干个规模更小的同类子问题,递子问题求解,归原问题的解。
例5 Sumdiv
思路:数论+分治
利用公式\(\sigma(n)=\prod \limits_i(\sum \limits_{0\leqslant j \leqslant \alpha_i} p_i^j)\)(其中\(n=\prod \limits_i p_i^{\alpha_i}\))(类比母函数,直接展开)
本题即要求\(\prod \limits_i(\sum \limits_{0\leqslant j \leqslant B*\alpha_i} p_i^j)\%9901\)(其中\(A=\prod \limits_i p_i^{\alpha_i}\))
即要能求\(\sum \limits_{0\leqslant i \leqslant c} p^i\)
为了使用分治法,我们最好先设一个状态来代表待求解的值,以保证子问题与原问题性质一致。
这里我们用\(S(p,c)\)代表\(\sum \limits_{0\leqslant i \leqslant c} p^i\).为使用分治法,我们需要将问题规模缩小,尝试将问题规模缩小至原来的\(\dfrac{1}{2}\).
对c的进行奇偶讨论:
若c为奇数,则求和式共有c+1项,平分后化作:
\(S(p,c)=\sum\limits_{0\leqslant i\leqslant \frac{c-1}{2}}p^i+\sum\limits_{\frac{c+1}{2}\leqslant i\leqslant c}p^i\)\(=\)\(\sum\limits_{0\leqslant i\leqslant \frac{c-1}{2}}p^i+p^{\frac{c+1}{2}}\sum\limits_{0\leqslant i\leqslant \frac{c-1}{2}}p^i\)\(=\)\((1+p^{\frac{c+1}{2}})\sum\limits_{0\leqslant i\leqslant \frac{c-1}{2}}p^i\)\(=\)\((1+p^{\frac{c+1}{2}})S(p,\dfrac{c-1}{2})\)
此处将\(p^i\)按大小顺序分为两组:求解的问题具有连续性,即p的指数连续递增;若按奇偶分组,则连续性被破坏。
若c为偶数,拆项转化可得:
\(S(p,c)=S(p,c-1)+p^c=(1+p^{\frac{c}{2}})S(p,\dfrac{c}{2}-1)+p^c\)
即可以在\(O(logc)\)时间内完成求和操作。
其中,\(p^c\)可采用快速幂完成。
同时,需要实现对n的唯一分解,采用试除法分解。
实现:
int qpow(int a, int b) { // 快速幂
int ans = 1;
for (; b; b >>= 1) {
if (b & 1)
ans = (long long)ans * a % MOD;
a = (long long)a * a % MOD;
}
return ans;
}
int sum(int p, int c) {
if (c == 0) // 边界
return 1;
if ((c & 1) == 1)
return (long long)(1 + qpow(p, (c + 1) / 2)) * sum(p, (c - 1) / 2) % MOD;
return ((long long)(1 + qpow(p, c / 2)) * sum(p, c / 2 - 1) % MOD +
qpow(p, c)) %
MOD;
}
int main() {
int a, b, S = 1, cnt = 0;
cin >> a >> b;
for (int i = 2; i * i <= a; i++) // 试除法唯一分解
if (a % i == 0) {
p[cnt] = i;
while (a % i == 0)
a /= i, c[cnt]++;
cnt++;
}
if (a > 1) // a为质数
p[cnt] = a, c[cnt++]++;
for (int i = 0; i < cnt; i++)
S = S * sum(p[i], b * c[i]) % MOD;
cout << S * (a != 0) << endl; // 特判a==0
return 0;
}
分形¶
例6 Fractal Streets
思路:分治
即要确定编号为M的房屋在N级城市中的位置,不妨以左上角为坐标原点建系表示其位置。
为了使用分治法,我们设该状态为\(P(N,M)=(x,y)\).由N级城市的构造方法可以看出其由4个不同形态的N-1级城市构成,故将问题规模缩小至\(P(N-1,M\%4^{N-1})\).
在将M缩至\(M\%4^{N-1}\)的同时,我们规定房子编号从0开始;这样,我们可以利用余数\(0\sim 4^{N-1}-1\)来指明该房屋在其所属小城市中的相对编号;若不规定编号从0开始,则因取模后不会产生\(4^{N-1}\)导致该房屋编号无法表达。
接下来的问题是考虑如何从\(P(N-1,M\%4^{N-1})=(x,y)\)中求得\(P(N,M)=(x',y')\).显然,我们要对M在N级城市中所属哪一个N-1级城市进行分类讨论。
以N=2为例,我们先将每个点分别取模,图示如下:
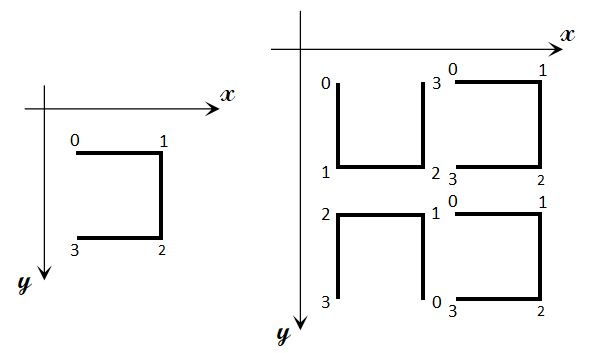
对于右上角的城市,显然\(\left\{\begin{array}{ll}x'=x+2^{N-1},\\y'=y\end{array}\right.\)
同理,对于右下角的城市,显然\(\left\{\begin{array}{ll}x'=x+2^{N-1},\\y'=y+2^{N-1}\end{array}\right.\)
对于左上角的城市,我们可以看作是由小城市关于\(y=x\)对称得到的,图示如下:
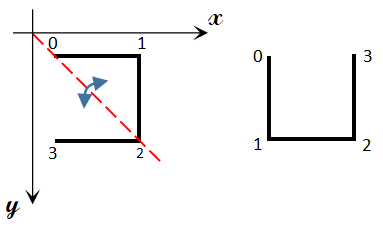
易知\(\left\{\begin{array}{ll}x'=y,\\y'=x\end{array}\right.\)
对于左下角的城市,我们可以看作是由小城市关于\(y=-x+2^{N-1}-1\)对称后平移得到的,图示如下:
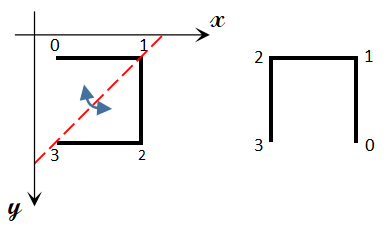
易知\(\left\{\begin{array}{ll}\dfrac{y+y''}{2}=-\dfrac{x+x'}{2}+2^{N-1}-1,\\\dfrac{y''-y}{x'-x}=1\\y'=y''+2^{N-1}\end{array}\right.\)
解得\(\left\{\begin{array}{ll}x'=2^{N-1}-1-y,\\y'=2^N-1-x\end{array}\right.\)
这样,我们只需要判断M属于N的哪个小城市即可。可以通过\(M/4^{N-1}\)进行判断。
当\(N\geqslant3\)时,可以将0,1,2,3看作N-1级城市的四个角,做的平移对称变换一致,都可利用上述式子进行计算。
实现:
struct coord { // 坐标
long long x, y;
};
coord pos(int n, long long m) {
coord ret, npos; // ret相当于(x',y'),npos相当于(x,y)
long long size = 1ll << (2 * (n - 1)), len = 1ll << (n - 1); // 1.
if (n == 0) { // 边界
ret.x = ret.y = 0;
return ret;
}
npos = pos(n - 1, m % size);
if (m / size == 0) {
ret.x = npos.y, ret.y = npos.x;
return ret;
}
if (m / size == 1) {
ret.x = npos.x + len, ret.y = npos.y;
return ret;
}
if (m / size == 2) {
ret.x = npos.x + len, ret.y = npos.y + len;
return ret;
}
ret.x = len - 1 - npos.y, ret.y = (len << 1) - 1 - npos.x;
return ret;
}
long long dis(coord a, coord b) {
return round(sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)) * 10); // 2.
}
int main() {
int n, N;
long long a, b;
cin >> n;
for (int t = 0; t < n; t++) {
cin >> N >> a >> b;
cout << dis(pos(N, a - 1), pos(N, b - 1)) << endl;
}
return 0;
}
细节:
1.1ll表示long long类型的1,否则直接计算将会导致计算结果的类型为int而溢出;由于\(4^{N-1}=2^{2(N-1)}\)和\(2^{N-1}\)多次使用,先将其计算好省去后续重复计算的时间。
2.两房屋中点间距离等于二者左上角之间的距离,利用两点间距离公式计算距离;round用于四舍五入。
递归的机器实现¶
总结:调用即入栈(未运行部分被压栈),返回即出栈(未运行部分继续运行);栈内保存局部变量和未完成部分
图示:
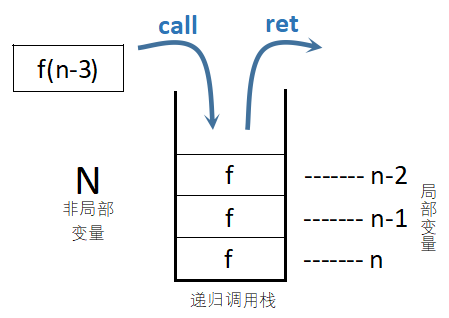
局部变量在每层递归中都占有一份空间,声明过多或递归过深就会超过栈所能存储的范围,造成栈溢出。
应用1:模拟实现形式,将递归改写为非递归
例7非递归实现组合型枚举
思路:模拟
模拟递归的实现形式,维护一个递归调用栈用来保存局部变量和运行状态,按调用即入栈,返回即出栈的规律将递归改写为循环:递归结束的标志是完全返回,即递归调用栈为空,故将栈非空作为while循环的条件。
栈内数据存储:
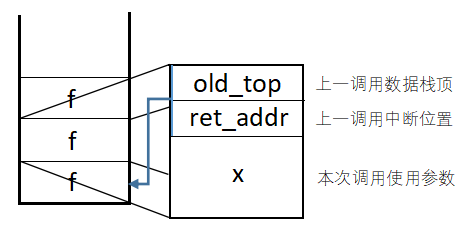
由于我们每次调用时执行入栈操作,所以关于上一调用的运行状态需和本次调用的数据需一并保存;每次返回时需取出上一调用的运行状态,将其放在全局变量中实时更新当前调用运行状态。
实现:
const int N = 25 + 1, M = 4 * N + 5; // 栈深度最大为N,每一调用占用2+2个空间
int n, m, chosen[N], s[M], top, address, dep, k; // address为当前程序运行状态
void call(int dep, int k, int ret_addr) {
int old_top = top;
s[++top] = dep;
s[++top] = k;
s[++top] = ret_addr;
s[++top] = old_top;
}
int ret() {
int ret_addr = s[top - 1];
top = s[top]; // 将top更新为old_top
return ret_addr;
}
int main() {
cin >> n >> m;
call(1, 0, 0); // 0表示起始状态
while (top) { // 起始调用的old_top为0,top归零意味着起始调用结束
dep = s[top - 3], k = s[top - 2]; // 参数传递
switch (address) {
case 0:
if (dep > n + 1 || k + n - dep + 1 < m) {
address = ret(); // 返回时还原上一调用运行状态
continue; // 每次循环相当于一次函数运行过程,continue即结束当前调用的运行
}
if (k == m) {
for (int i = 0; i < k; i++)
cout << chosen[i] << " ";
cout << endl;
address = ret();
continue;
}
chosen[k] = dep;
call(dep + 1, k + 1, 1); // 此调用运行状态为即将运行至case 1处
address = 0; // 新调用默认从头开始
continue;
case 1:
call(dep + 1, k, 2); // // 此调用运行状态为即将运行至case 1处
address = 0;
continue;
case 2:
address = ret();
continue;
}
}
}
由此,我们可以总结出递归转循环的一般方法:
1.维护一个栈,并实现对应的call()和ret()
2.运行状态的划分:由于每次调用会导致未运行部分压栈,所以以调用为界划分运行状态:
递归写法:
int dfs(int dep){
/*
case 0
*/
dfs(dep+1);
/*
case 1
*/
dfs(dep+2);
/*
case 2
*/
//...
dfs(dep+k);
/*
case k
*/
}
对应循环写法:
while (top){
// 参数传递
switch(address){
case 0:
/*
case 0
*/
call(dep+1, 1);
address = 0;
continue;
case 1:
/*
case 1
*/
call(dep+2, 2);
address = 0;
continue;
case 2:
/*
case 2
*/
call(dep+3, 3);
address = 0;
continue;
//...
case k:
/*
case k
*/
address = ret();
continue;
}
}
应用2:用全局变量维护局部变量
用于只能同时执行一个调用,每次调用只会用到一组局部变量,所以我们可以将全局变量做同步更新,从而不使用局部变量。
例如将例2改写为不用局部变量的版本: