贪心

定义：在每次决策时采取当前意义下最优策略的算法

思想：局部最优导出整体最优

关键：

1. 局部

贪心算法从局部到整体的思想，事实上是将原问题划分成了多个结构一致，规模不同的子问题。

如图，我们在原问题的基础上做出相应的决策，从而将问题转化为具有相似结构的更小的子问题。

类似的，这种思想见于递归。

2. 最优

事实上，确保子问题结构与原问题一致，是为了在子问题上继续采取相同的决策；故进行当前决策时，我们可以将子问题看作最优化状态，只考虑如何在子问题与原问题之间做出决策，使得原问题取到当前的最优结果。

3. 导出

与动态规划不同的是，贪心算法是“一次性”的，每个决策只会做出一次，这意味着决策一旦做出，便无法再修改。故贪心算法的正确性需要证明。

能够采用贪心算法的问题一般都具有如下两个性质：

• 贪心选择性(Greedy choice property)

  所有的决策只能依赖于已经做出的决策，且决策一旦做出，便无法修改。这是贪心算法解决问题的形式，只有能够按照这样的形式分阶段一步步做出决策的问题才能运用贪心算法

• 最优子结构(Optimal substructure)

  当前问题的最优解包含了子问题的最优解；换句话说，选择当前问题的最优解并不会干扰子问题的求解。如数字三角形问题：

  

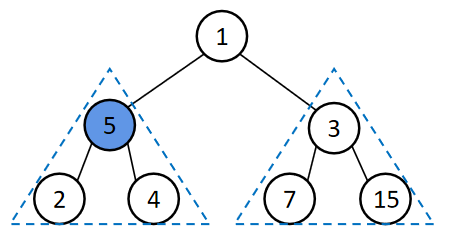
  按照贪心对子问题最优化的假设，从根节点出发后，贪心算法认为此时子结构已经达到最优化的选择，故在此基础上，只需选择5即可使全局达到最优。而问题出在对5的选择，会导致子问题无法取得最优，即选择当前的最优解5，并不包含子问题的最优解(1-3)-15.

  我们知道这种问题可以用动态规划进行求解。不同于贪心，动规将从问题的边界——叶子节点出发向上汇总答案。按照这样顺序的划分具有最优子结构性质。但对于贪心而言，通过做出一次决策使问题缩小为子问题的形式，是无法按动规从下至上的顺序进行的；从贪心算法的角度来看动规做出的决策过程，是依赖于子问题信息的(\(\underbrace{f_{x}}_{Ori}=a_{x}+\underbrace{\max\{f_{x.lson},f_{x.rson}\}}_{Sub}\))，所以并不具有贪心选择性。

在具有这些性质的问题上，往往能够保证局部最优能够导出整体最优。

如前所述，一旦我们能按照贪心的步骤来处理问题，那么该问题就已经具有了贪心选择性。我们只需要证明该问题具有最优子结构，这包含两重含义：确定最优选择方案（贪心策略），证明贪心策略对子问题取得最优无干扰。

围绕这一目标，原书给出的证明手段2-5是统一的，一般步骤如下：

1. 考虑问题求解过程中的任一阶段，并按照选定的贪心策略\(A\)做出决策
2. 假设存在一个更优化的决策\(O\)
3. 分别将\(A,O\)作用在当前局面上，得到子问题\(sub_A,sub_O\)
4. 证明若\(sub_O\)能够取得最优解\(K\)，则\(sub_A\)能取得不坏于\(K\)的解\(K'\)，同时，在当前局面上，\(A\)的贡献\(v_A\)不小于\(O\)的贡献\(v_O\)，即证明\(sub_A+v_A\geqslant sub_O+v_O\)
5. 从而决策\(O\)并不优于决策\(A\)，与假设矛盾

这里体现了如下的数学思想：

1. 数学归纳法：根据贪心选择性，决策分阶段一步步进行，符合数学归纳法的形式；选定求解过程中的任一阶段，同时考虑其子问题的结果的做法运用了数归
2. 反证法：这里利用反证法证明不存在更优策略\(O\)，从而证明策略\(A\)的最优性质
3. 范围缩放/决策包容性：在不同规模的原问题与子问题上进行考虑，并考虑当前策略对子问题的影响，正是从这一角度出发进行考量的

至于原书给出的手段1，适用于排序问题对“最优”策略的决定。

排序问题求解的核心，是确认衡量不同元素间大小关系的“标准”。从这一角度看，微扰能解出用于比较的合适参量。

我们也可以从另一个角度出发来划分排序问题求解的阶段。任何排序终止于逆序对归零，我们每一阶段做出的操作，便是对原序列（给定或随机生成）中的逆序元素进行交换。而对于两个不相邻元素的交换，我们可以将其分解为多次的相邻元素交换，即“微扰”。微扰后，倘若总体贡献增加，我们就认为原先两个元素为“逆序”。这样，每次的相邻交换仅使得在最优化意义下的逆序数减少，并不会对子问题（即交换完某一逆序后的序列）的求解造成干扰；同样的，由于逆序数终将减少为零，所以在当前交换哪一对逆序，并不影响最终问题的求解。事实上，当我们分析出衡量标准后，直接按该标准对原序列进行排序即可。

最优策略的确定：由于选定的最优策略将在不同规模的问题上进行作用，同时划分出子问题，还需保证对子问题没有后效性的影响，我们一般考虑“极端”的选择，即策略一般含有“最大/最小”之类的字眼。

例1 Sunscreen

思路：贪心

贪心策略：选择当前minSPF最大的牛，并给它涂上所能用的SPF最大的防晒霜

证明：

记当前策略为\(A\).考虑求解过程中的任一阶段，假设存在一个更优的策略\(O\).对策略\(A\)取反，有 $$ A=\max minSPF \land\max SPF\ \lnot A=\lnot\max minSPF \lor\lnot\max SPF $$ 即我们考虑这两类策略：(1)\(O_1\)：不选择当前minSPF最大的牛 (2)\(O_2\)：不给选定的牛涂SPF最大的防晒霜。为了控制变量，考虑\(O_1\)的同时所选的牛涂所能用的SPF最大的防晒霜，考虑\(O_2\)时选择minSPF最大的牛。

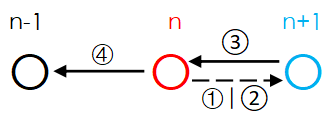
对于\(O_1\)，不妨考虑每次选择当前minSPF次大的牛，对于当前minSPF最大的牛i与次大的牛i-1，如图（其中K为除去两头牛的子问题的最优解）：

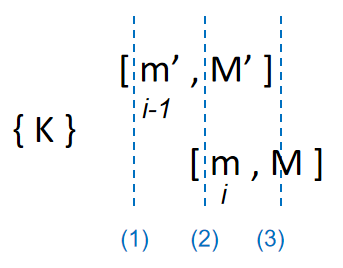
策略\(A\)将选择牛i，而\(O_1\)将选择牛i-1.针对两头牛可用防晒霜范围不同，将有如图所示的三种防晒霜，现考虑具有其中的两瓶（保证两头牛都有的涂），情况如下表（为了防止重复，设I\(\leqslant\) II）：

防晒霜I	防晒霜II	策略A	\(sub+v\)	策略\(O_1\)	\(sub+v\)
1	2	2	(K+1)+1	1	K+1
	3	3	(K+1)+1	1	K+1
2	2	2	(K+1)+1	2	K+1
	3	3	(K+1)+1	2	K+1

事实上，由于我们保证两头牛都有的涂，在\(A\)之后的子问题上，可以继续选择牛i-1，并再进入与\(O_1\)之后相同的子问题中。不难看出，\(O_1\)并不优于\(A\).

注：

1. 考虑子问题最优解K时，我们并不关心子问题采取的是何种策略；事实上，我们可用将K视为关于问题规模的函数，且K关于规模的递增是不减的
2. 或许你会认为，策略\(O_1\)选择i-1后，子问题仍然可以选择i，但这与我们对子问题的规定相悖：在策略\(O_1\)做出选择后，原问题被划分为了规模更小的相同结构的子问题，意味着牛i并不在我们的子问题中；另一个角度看，从本质上来说，我们决定了决策顺序，由于贪心选择性“所有的决策只能依赖于已经做出的决策”，故合理的决策顺序是十分重要的。为了保持子问题的结构一致性，我们需要按照特定的大小顺序来选择当前的决策对象，这是贪心算法本身的性质导致的，我们只能按照特定的顺序来划分子问题。故下文不再对决策顺序进行讨论

对于\(O_2\)，不妨选择SPF次大的防晒霜。将上图的i,i-1牛理解为相邻两次决策的对象（分别为前后两个局面的minSPF最大的牛，保证当前决策对象牛i有两瓶SPF不相等的防晒霜可以涂），情况如下表：

防晒霜I	防晒霜II	策略A	\(sub+v\)	策略\(O_2\)	\(sub+v\)
2	3	3	(K+1)+1	2	K+1

其余情况二者做出的决策无差别。显然，\(O_2\)亦不优于\(A\).

综上，\(O\)并不优于\(A\)，矛盾！故贪心策略正确性得证。

因此，我们只需要将牛按照minSPF递减排序，依次选择每头牛可用SPF最大的防晒霜即可。

上述讨论中，我们并未利用maxSPF进行决策，事实上，如下的贪心决策同样正确：选择当前maxSPF最小的牛，并给它涂上所能用的SPF最小的防晒霜，如图：

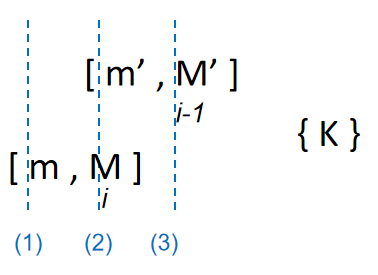
验证方法同上。

实现1：降序选最大

pair<int, int> cow[N], spf[N];
int main() {
  int c, l, a, b, ans = 0;
  cin >> c >> l;
  for (int i = 0; i < c; i++) {
    cin >> a >> b;
    cow[i] = make_pair(a, b); // minSPF, maxSPF
  }
  for (int i = 0; i < l; i++) {
    cin >> a >> b;
    spf[i] = make_pair(a, b); // SPF, cover
  }
  sort(cow, cow + c, greater<pair<int, int>>()); // 降序
  sort(spf, spf + l, greater<pair<int, int>>());
  for (int i = 0; i < c; i++) {
    for (int j = 0; j < l; j++)
      if (spf[j].second && spf[j].first <= cow[i].second &&
          spf[j].first >= cow[i].first) { // 寻找SPF最大的可用防晒霜
        spf[j].second--, ans++;
        break;
      }
  }
  cout << ans << endl;
  return 0;
}

实现2：增序选最小

pair<int, int> cow[N], spf[N];
int main() {
  int c, l, a, b, ans = 0;
  cin >> c >> l;
  for (int i = 0; i < c; i++) {
    cin >> a >> b;
    cow[i] = make_pair(b, a); // 为了对maxSPF进行排序
  }
  for (int i = 0; i < l; i++) {
    cin >> a >> b;
    spf[i] = make_pair(a, b);
  }
  sort(cow, cow + c);
  sort(spf, spf + l);
  for (int i = 0; i < c; i++) {
    for (int j = 0; j < l; j++)
      if (spf[j].second && spf[j].first <= cow[i].first &&
          spf[j].first >= cow[i].second) {
        spf[j].second--, ans++;
        break;
      }
  }
  cout << ans << endl;
  return 0;
}

例2 Stall Reservations

思路：贪心

贪心策略：选择当前开始时间最早的牛（子问题划分标准），并将它安排在结束时间最早的畜栏中（决策内容）

证明：

记上述策略为\(A\)，策略\(O\)将牛放在结束时间次早的畜栏中。

假设现在有两个畜栏\(i,j\)可供我们选择，对于当前的决策对象牛\(p\)，策略\(A\)选择结束时间最早的畜栏\(i\)，而策略\(O\)选择结束时间次早的畜栏\(j\).由于决策顺序按照开始时间递增，故在未放置牛\(p\)的情况下，畜栏\(i,j\)对后面所有牛均可用，并不会出现更优解。

从另一个角度来看，为了将这头牛放下， 我们应该考虑当前结束时间最早的畜栏，倘若结束时间最早的畜栏都不能容纳这头牛的话，将没有畜栏能够容纳它。

故算法正确性得证。

所以我们只要将牛按照开始时间进行排序，依次考虑每头牛，我们选取当前结束时间最早的畜栏将其放入；倘若放不下，则新开一个畜栏将其放入。

我们可以利用小根堆（优先队列）来维护结束时间最早的畜栏，从而将复杂度优化至\(O(n\log n)\).

同样的，我们也可以选择当前结束时间最晚的牛，原理同上。从结构上来说，两种策略在本质上呈对称关系。

实现1：按开始时间递增

pair<pair<int, int>, int> cow[N]; // (开始时间, 结束时间), id
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q; // 小根堆
int main() {
  int n, a, b, cnt = 1;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> a >> b;
    cow[i] = make_pair(make_pair(a, b), i);
  }
  sort(cow, cow + n);
  q.push(make_pair(cow[0].first.second, cnt)); // 结束时间, id
  ans[cow[0].second] = cnt;
  for (int i = 1; i < n; i++) {
    auto p = q.top();
    if (p.first < cow[i].first.first) {
      q.pop();
      q.push(make_pair(cow[i].first.second, p.second));
      ans[cow[i].second] = p.second;
    } else {
      q.push(make_pair(cow[i].first.second, ++cnt));
      ans[cow[i].second] = cnt;
    }
  }
  cout << cnt << endl;
  for (int i = 0; i < n; i++)
    cout << ans[i] << endl;
  return 0;
}

实现2：按结束时间递减

pair<pair<int, int>, int> cow[N];
priority_queue<pair<int, int>, vector<pair<int, int>>> q;
int main() {
  int n, a, b, cnt = 1;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> a >> b;
    cow[i] = make_pair(make_pair(b, a), i);
  }
  sort(cow, cow + n, greater<pair<pair<int, int>, int>>());
  q.push(make_pair(cow[0].first.second, cnt));
  ans[cow[0].second] = cnt;
  for (int i = 1; i < n; i++) {
    auto p = q.top();
    if (cow[i].first.first < p.first) {
      q.pop();
      q.push(make_pair(cow[i].first.second, p.second));
      ans[cow[i].second] = p.second;
    } else {
      q.push(make_pair(cow[i].first.second, ++cnt));
      ans[cow[i].second] = cnt;
    }
  }
  cout << cnt << endl;
  for (int i = 0; i < n; i++)
    cout << ans[i] << endl;
  return 0;
}

例3 Radar Installation

思路：贪心

先将原问题进行转化，对于点\((x_i,y_i)\)，我们将其转化为\(x\)轴上的管辖区间\([l_i,r_i]\)，如图：

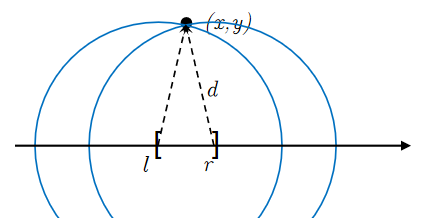
由勾股定理易得 $$ \left{ \begin{array}{ll} l=x-\sqrt{d^2-y^2}\ r=x+\sqrt{d^2-y^2} \end{array} \right. $$ 问题转化为：对于多个区间，选择合适的点，使得每个区间中都至少含有一个点。显然，当\(y>d\)时，原问题无解。

贪心策略：选择当前\(l\)最小的区间（子问题划分标准），若上次放置的点（可通过调整）可用，则（通过适当调整）继续使用上次的点；若上次放置的点不可用，则新设一个点，并将其放置于区间的末尾\(r\)处 （决策内容）

具体而言，调整意味着将点的位置\(pos\)改为\(min(pos,r)\)，如下图：

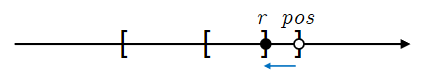
这样，经过调整，该点可为当前考虑的区间所使用，且符合位于区间末尾的要求。

证明：

记上述策略为\(A\)，策略\(O_1\)为当上次放置的点可用时，仍然选择新开一个点，策略\(O_2\)为每次新设点时不将其放在区间末尾。

对于\(O_1\)，由于新设点会对子问题造成影响，我们对子问题的种类进行讨论，如下表：

当前点	新设点	\(sub_A+v_A\)	\(sub_O+v_O\)
下一个区间能用	下一个区间能用	K+0	K+1
下一个区间不能用	下一个区间能用	(K+1)+0	K+1
	下一个区间不能用	(K+1)+0	(K+1)+1

注：我们只需要考虑能否被下一个区间利用，若能被后续1+n个区间利用，则策略\(A\)在子问题上新设的点同样能用于后续的n个区间

可见，策略\(O_1\)并不优于策略\(A\).

对于\(O_2\)，由于\(A\)将点设在更靠后的位置，能被子问题更加充分的利用，故策略\(O_2\)并不优于策略\(A\).

综上，即证。

与前两题类似，本题同样存在一个结构上对称（可以理解为关于直线\(x=0\)对称）的策略，不再赘述。

实现：

pair<double, double> range[N]; // l, r
int main() {
  int n, d, x, y, ans = 0;
  double pos = -INF;
  cin >> n >> d;
  for (int i = 0; i < n; i++) {
    cin >> x >> y;
    if (y > d) {
      cout << -1 << endl;
      return 0;
    }
    range[i].first = x - sqrt(d * d - y * y);
    range[i].second = 2 * x - range[i].first;
  }
  sort(range, range + n);
  for (int i = 0; i < n; i++) {
    if (range[i].first <= pos)
      pos = min(pos, range[i].second);
    else
      ans++, pos = range[i].second;
  }
  cout << ans << endl;
  return 0;
}

例4 国王游戏

思路：微扰+高精

按照正文的分析，我们通过微扰法来确认大臣们排序的标准。事实上，对任意两个相邻大臣\(i,i+1\)的交换，并不会影响其余的大臣，因为交换\(i,i+1\)并不影响\(\prod\limits_{j=0}^k a_j(1\leqslant k<i,i+1<k\leqslant n)\)；而交换非相邻的大臣，都可以转换为多次交换相邻大臣。

一个交换是有效的，当且仅当它减小了整体收益的最大值；又因为除交换的双方外，其余人的收益不发生改变，故只需这个交换减小了交换双方整体收益的最大值，即

\[ \max(\dfrac{\prod\limits_{j=0}^{i-1}a_j}{b_i},\dfrac{\prod\limits_{j=0}^ia_j}{b_{i+1}})>\max(\dfrac{\prod\limits_{j=0}^{i-1}a_j}{b_{i+1}},\dfrac{a_{i+1}\prod\limits_{j=0}^{i-1}a_j}{b_i})\\ \Leftrightarrow\prod\limits_{j=0}^{i-1}a_j*\max(\dfrac{1}{b_i},\dfrac{a_i}{b_{i+1}})>\prod\limits_{j=0}^{i-1}a_j*\max(\dfrac{1}{b_{i+1}},\dfrac{a_{i+1}}{b_i})\\ \Leftrightarrow\max(\dfrac{1}{b_i},\dfrac{a_i}{b_{i+1}})>\max(\dfrac{1}{b_{i+1}},\dfrac{a_{i+1}}{b_i})\\ \Leftrightarrow\max(b_{i+1},a_ib_i)>\max(b_i,a_{i+1}b_{i+1})\\ \Leftrightarrow \left\{ \begin{array}{ll} b_{i+1}>a_ib_i\\ b_{i+1}>b_i\\ b_{i+1}>a_{i+1}b_{i+1} \end{array} \right. Or \left\{ \begin{array}{ll} a_ib_i>b_{i+1}\\ a_ib_i>b_i\\ a_ib_i>a_{i+1}b_{i+1} \end{array} \right. \]

又\(a,b\in\mathbb N^+\)，所以\(b_{i+1}\leqslant a_{i+1}b_{i+1},b_i\leqslant a_ib_i\)（无所谓是否取等，取等时只是没必要交换，但交换并不会导致错误的结果），故 $$ a_ib_i>a_{i+1}b_{i+1}>b_{i+1} $$ 所以，当相邻两大臣满足\(a_ib_i>a_{i+1}b_{i+1}\)时，交换是有效的。故排序标准是\(ab\)，按从小到大的顺序进行排序。

注意，最后要求出最小的最大收益的具体值，而\(a^n\)的上限明显超出了int能存储的范围，需高精（高精乘高精、高精除低精）。

实现：

高精：这里采用压4位、vector存储的部分实现

struct number {
  int len;
  vector<int> n;
  number &operator=(const char *);
  number &operator=(int);
  number();
  number(int);
  bool operator<(const number &) const;
  number operator*(const number &) const;
  number operator/(const int &) const;
  number &operator*=(const number &);
};

number &number::operator=(const char *c) {
  n.clear();
  len = 1;
  int l = strlen(c), k = 1, tmp = 0;
  for (int i = 1; i <= l; i++) {
    if (k == 10000) {
      n.push_back(tmp);
      len++, k = 1, tmp = 0;
    }
    tmp += k * (c[l - i] - '0');
    k *= 10;
  }
  n.push_back(tmp);
  return *this;
}

number &number::operator=(int a) {
  char s[15];
  sprintf(s, "%d", a);
  return *this = s;
}

number::number() {
  n.clear();
  n.push_back(0);
  len = 1;
}

number::number(int n) { *this = n; }

bool number::operator<(const number &b) const {
  if (len != b.len)
    return len < b.len;
  for (int i = len - 1; i >= 0; i--)
    if (n[i] != b.n[i])
      return n[i] < b.n[i];
  return false;
}

number number::operator*(const number &b) const {
  number c;
  c.len = len + b.len + 1;
  for (int i = 0; i < c.len; i++)
    c.n.push_back(0);
  for (int i = 0; i < len; i++)
    for (int j = 0; j < b.len; j++) {
      c.n[i + j] += n[i] * b.n[j];
      c.n[i + j + 1] += c.n[i + j] / 10000;
      c.n[i + j] %= 10000;
    }
  while (c.n[c.len - 1] == 0 && c.len > 1) {
    c.len--;
    c.n.pop_back();
  }
  return c;
}

number &number::operator*=(const number &b) { return *this = *this * b; }

number number::operator/(const int &b) const {
  long long tmp = 0;
  number c;
  c.len = len;
  for (int i = 0; i < c.len; i++)
    c.n.push_back(0);
  for (int i = len - 1; i >= 0; i--) {
    tmp = tmp * 10000 + n[i];
    c.n[i] = tmp / b;
    tmp %= b;
  }
  while (c.n[c.len - 1] == 0 && c.len > 1) {
    c.len--;
    c.n.pop_back();
  }
  return c;
}

ostream &operator<<(ostream &o, number &a) {
  o << a.n[a.len - 1];
  for (int i = a.len - 2; i >= 0; i--) {
    o.width(4);
    o.fill('0');
    o << a.n[i];
  }
  return o;
}

istream &operator>>(istream &i, number &a) {
  char s[15];
  i >> s;
  a = s;
  return i;
}

算法主体：

const int N = 1e3 + 5;
pair<number, pair<int, int>> minister[N];

int main() {
  int n, ka, kb, a, b;
  number tmp, ans = 0;
  cin >> n >> ka >> kb;
  for (int i = 0; i < n; i++) {
    cin >> a >> b;
    tmp = a * b;
    minister[i] = make_pair(tmp, make_pair(a, b));
  }
  sort(minister, minister + n);
  tmp = ka; // 国王
  for (int i = 0; i < n; i++) {
    ans = max(ans, tmp / minister[i].second.second);
    tmp *= minister[i].second.first;
  }
  cout << ans << endl;
  return 0;
}

例5 Color a Tree

思路：微扰

解决问题的关键在于确定合理的染色顺序。

对于权值最大的点，一定会在它能被染的第一时间染上色。假设我们现在能染权值最大的点\(i\)，却染了另外一个点\(j\)，那么推迟\(k\)次染\(i\)的代价为\(kw_i>kw_j\)，即让点\(j\)先染并不优于先染点\(i\).

而由于题目的规定，点\(i\)能被染，当且仅当它的父节点被染色。所以点\(i\)一定是紧接着父节点进行染色的。进一步的，我们可以把所有具有“紧接”关系的点缩成一个“超级点”，当我们一旦选择染这个“超级点”，就会按照我们已经规定好的顺序一口气染完里面所有的点。

注意“超级点”一口气染完这个性质。由于我们在安排顺序时是面向所有的点进行选择的，故两个“超级点”染色时是不可能出现交叉染色的情况的，一定是将一个超级点染完，再染下一个超级点；否则将与超级点的定义相矛盾。

现在问题转化为决定两个超级点染色的先后顺序，按照正文的思路，我们采取微扰法。

注：为了书写的便捷，下面的推导将\(w_i\)记作\(i\)

假设现在有两个超级点\(A,B\)（都处于能被染色的第一时间），其中超级点\(A\)由\(a_1,a_2,\cdots,a_n\)合并而来（\(a_1,\cdots,a_n\)按内部染色顺序排列），超级点\(B\)由\(b_1,b_2,\cdots,b_m\)合并而来，并设当前已经染了\(k\)个点。则先染超级点\(A\)，当且仅当按照顺序\(AB\)染色的代价小于按照顺序\(BA\)染色的代价，即 $$ \sum\limits_{i=1}^n(k+i)a_i+\sum\limits_{i=1}^m(k+n+i)b_i<\sum\limits_{i=1}^m(k+i)b_i+\sum\limits_{i=1}^n(k+m+i)a_i $$ 将常数\(n,m,k\)提出，我们有

\[ k\sum\limits_{i=1}^na_i+\sum\limits_{i=1}^nia_i+k\sum\limits_{i=1}^mb_i+n\sum\limits_{i=1}^mb_i+\sum\limits_{i=1}^mib_i<k\sum\limits_{i=1}^mb_i+\sum\limits_{i=1}^mib_i+k\sum\limits_{i=1}^na_i+m\sum\limits_{i=1}^na_i+\sum\limits_{i=1}^nia_i\\ \Leftrightarrow n\sum\limits_{i=1}^mb_i<m\sum\limits_{i=1}^na_i\\ \Leftrightarrow \dfrac{\sum\limits_{i=1}^mb_i}{m}<\dfrac{\sum\limits_{i=1}^na_i}{n}\Leftrightarrow \bar{a}<\bar{b} \]

其中倒数第二步按照\(A,B\)各自具有的参量进行整理。由此我们看出，超级点内所有点权值的平均值是我们决定染色先后顺序的标准。这样我们可以按照平均值大小关系将先被染色的点并入它的父节点中形成新的超级点，并入后父节点的权值更新为这个新超级点权值的平均值。

由于根节点没有父节点，不对其进行合并操作。由于每次合并都会导致总点数减一，经过\(n-1\)轮的合并后，所有的点都被并入根节点，在根节点中，所有点的染色顺序便确定了。

所以我们的解题步骤是，选取当前代价最大的点（在合并阶段，不考虑此时是否可以染色，只考虑点的相对位置关系），将其合并到父节点中，并更新父节点的权值信息；不断重复上述操作\(n-1\)次，直到所有的点完成合并。

由于我们同时需要维护父子关系，每次合并时，将会影响并入的点\(i\)及\(i\)的子节点\(ch_i\)，\(ch_i\)的父节点将变为\(fa_i\)，我们在合并时同步更新。而点\(i\)并入父节点后我们无需再对其进行考虑，只需将其权值置负便不会对算法进程造成影响。

但直接按照这样的步骤来操作，将难以对染色顺序进行维护，总代价也不易求。我们可以换一个思路来求总代价。以三个点\(a,b,c\)为例，当我们没有按照任何顺序，独立染色时，初始代价为\(a+b+c\).

现在，我们让\(c\)排在\(a\)的后面，则\(c\)会产生“等待代价”\(1*c\)，这时的总代价更新为\(a+b+c+c=a+b+2c\).

继续，我们将\(b\)排在\(a,c\)的后面，则\(b\)会产生相应的“等待代价”\(2*b\)，这是总代价更新为\(a+b+2c+2b=a+3b+2c\).

可见，每次确定顺序，就会产生相应的等待代价。一般地，将总权值为\(\sum\limits w\)的超级点确定到含有\(n\)个点的超级点后面，将产生\(n\sum\limits w\)的“等待代价”；当所有的顺序都被确定下来后，总的等待代价也就计算出来了。

按照总代价=初始代价+等待代价的思路，我们可以在合并时计算总代价。每一次合并过程都是一次确定顺序的过程，将\(i\)合并至\(fa_i\)，会产生\(|fa_i|\sum\limits_{a\in i}w_a\)的等待代价，将其累计到总代价中，便在合并完成时同时得到染色的总代价。

事实上，我们并不用将所有的点看作一棵树，我们关心的只是每个点的父节点而已。

下以样例为例图解合并过程：

初始状态：

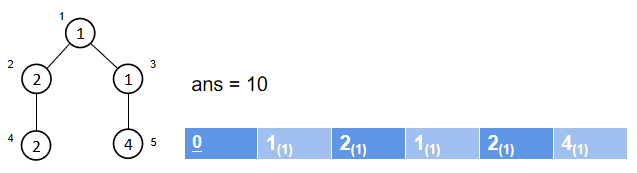
其中点的右上角时点的编号，点从1开始编号，故0号位空缺；点内数字是点的权值。表格中\(w_n\)代表该（超级）点总权值为\(w\)，共有\(n\)个点。

此时总代价为初始代价。

第一次合并：

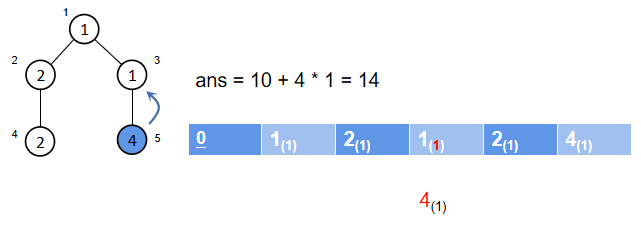
权值最大的5号点被并入父节点3中，并将5号点的权值乘以3号点的大小作为等待代价累计入答案。

同时更新3号点的信息，并将5号点置负，如下图。

第二次合并：

第三次合并：

注意，由于此时2号点有子节点4，需同步更新子节点4的父亲为1.

第四次合并：

终止状态：

实现：

struct Node {
  int fa, n = 1, w; // n为含有的点个数,w为含有点的总权值
  double avg;
} node[N];
int main() {
  int n, r, a, b, ans = 0, id, fa;
  cin >> n >> r;
  for (int i = 1; i <= n; i++) {
    cin >> node[i].w;
    node[i].avg = node[i].w;
    ans += node[i].w; // 累计初始代价
  }
  for (int i = 0; i < n - 1; i++) {
    cin >> a >> b;
    node[b].fa = a;
  }
  double avg;
  for (int i = 0; i < n - 1; i++) { // 处理n-1次即完成合并
    avg = -1;
    for (int j = 1; j <= n; j++) { // 寻找avg最大的点id
      if (j == r) // 根节点没有父节点,不并入
        continue;
      if (node[j].avg > avg)
        avg = node[j].avg, id = j;
    }
    fa = node[id].fa;
    ans += node[id].w * node[fa].n; // 累计等待代价
    node[fa].n += node[id].n, node[fa].w += node[id].w; // 更新父节点信息
    node[fa].avg = 1.0 * node[fa].w / node[fa].n;
    node[id].avg = -1; // 将并入的点权值置负,不再理会
    for (int j = 1; j <= n; j++) // 更新id子节点的fa
      if (node[j].fa == id)
        node[j].fa = fa;
  }
  cout << ans << endl;
  return 0;
}