总结与练习1¶
T1 The Pilots Brothers' Refrigerator
思路:枚举+位运算
与0x02节费解的开关不同的是,本题的状态空间较小,16个开关共有\(2^{16}\)中状态,可以全部进行枚举。
同样的,我们采用二进制状压的手法来完成指数型枚举,我们让状态参量\(S\)走遍\([0,2^{16}-1]\),而\(S\)在二进制表示下第\(i\)位为1意味着对\(i\)对应位置进行操作。
为了便于状压,我们将棋盘编号如下:
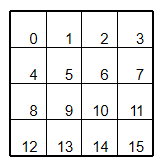
这样,我们便可以利用变量state将棋盘当前的状态保存起来,其中state的二进制表示中第\(i\)位为1代表该处为'+',0代表该处为'-'.同样的,\(S\)的第\(i\)位同样指操作棋盘的对应位置。
由于异或操作可以看作是一种切换,我们可以将行操作和列操作用数字表示,在实际操作时与当前状态进行异或即可,如图:
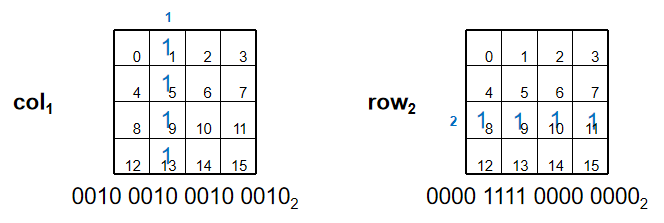
这样,我们只需要与0x1111,0x1111<<1,0x1111<<2,0x1111<<3异或就可以实现对第0,1,2,3列的切换,与15,15<<4,15<<8,15<<12异或就可以实现对第0,1,2,3行的切换。
注:16进制下1位代表4个二进制位;题目描述中行列从1开始编号,输出时需做相应转化
而编号\(i\)对应的行列号分别是\(i/4,i\%4\).这样,我们每次只需要将状态分别与\(col_i,row_i\)和1<<\(i\)异或即可。(\(i\)位置在行列切换中发生重复切换)当操作完成后,若棋盘状态归零,则得出最终答案。
实现:
char c;
int state = 0, cur, cnt;
for (int i = 0; i < 16; i++) {
c = getchar();
if (c == '\n')
c = getchar();
state |= (c == '+') << i; // 填充状态
}
for (int S = 0; S < 1 << 16; S++) {
cur = state, cnt = 0;
for (int i = 0; i < 16; i++) // 解析枚举状态
if (S & (1 << i))
cur ^= row[i / 4], cur ^= col[i % 4], cur ^= 1 << i, cnt++;
if (!cur) {
cout << cnt << endl;
for (int i = 0; i < 16; i++)
if (S & (1 << i))
cout << 1 + i / 4 << ' ' << 1 + i % 4 << endl;
return 0;
}
}
T2 占卜DIY
思路:模拟
由于每次从牌堆底部取牌,可以考虑开12个栈来模拟牌堆,对于最后一堆牌直接边读边处理即可。
实现:
const int N = 13;
stack<int> s[N];
int cnt[N], cur, tmp, ans;
int convert(char c) { // 片面字符 -> 数字
if ('0' < c && c <= '9')
return c - '0';
else if (c == '0')
return 10;
else if (c == 'J')
return 11;
else if (c == 'Q')
return 12;
else if (c == 'K')
return -1;
else
return 1;
}
int main() {
char c;
for (int i = 1; i < N; i++)
for (int j = 0; j < 4; j++) {
c = getchar();
if (c == ' ' || c == '\n')
c = getchar();
s[i].push(convert(c));
}
for (int i = 0; i < 4; i++) {
c = getchar();
if (c == ' ' || c == '\n')
c = getchar();
cur = convert(c);
if (cur != -1) // 最后一堆牌也算明牌
cnt[cur]++;
while (cur != -1) {
tmp = s[cur].top();
s[cur].pop(), cnt[tmp]++, cur = tmp;
}
}
for (int i = 1; i < N; i++)
if (cnt[i] == 4)
ans++;
cout << ans << endl;
return 0;
}
T3 Fractal
思路:递归
为了利用分形和好的结构性质,我们无法按照正常的行顺序进行打印。由于题目规模较小,我们可以将图形暂存到数组中。
递归边界为\(n=1\).下面来寻找规模\(n\)与\(n-1\)之间的关系。
以\(n=3\)为例,如图,它可以被看作5个\(n=2\)子块:
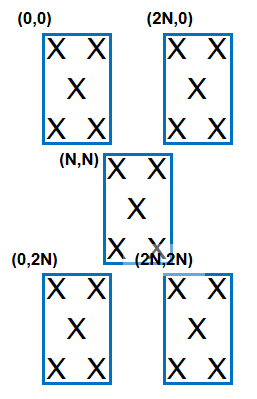
为了对子块进行定位,我们选定块的右上角为锚点,用锚点坐标来代替子块坐标,记子块的边长为\(N\),则以左上角为原点的坐标系中五个子块的坐标为 $$ (0,0),(2N,0),(N,N),(0,2N),(2N,2N) $$ 当左上角的实际坐标为\((x,y)\)时,与之叠加即可。
现在我们的问题转化为求子块的边长\(N\)。更一般的,我们来求块\(n\)的大小\(N_n\),则子块大小为\(N_{n-1}\).不难发现,当\(n=1\)时\(N=1\),\(n=2\)时\(N=3\),\(n=3\)时\(N=9\).事实上,从图中我们也能看出它们的递推关系\(N_k=3N_{k-1}\),不难求出\(N_{n-1}=3^{n-2}\).
值得注意的是,由于\(n\leqslant 7\),我们可以预处理出\(n=7\)的图形,然后对于多组询问,直接输出左上角的相应子块即可。
实现:
const int N = 1e3 + 5; // 3^6 = 729
const int delta[][2] = {{0, 0}, {2, 0}, {1, 1}, {0, 2}, {2, 2}}; // 增量系数
bool pic[N][N];
void dfs(int n, int x, int y) {
if (n == 1) {
pic[x][y] = 1;
return;
}
int size = pow(3, n - 2);
for (int i = 0; i < 5; i++)
dfs(n - 1, x + delta[i][0] * size, y + delta[i][1] * size);
}
int main() {
int n;
dfs(7, 0, 0); // 预处理
while (true) {
cin >> n;
if (n == -1)
break;
n = pow(3, n - 1);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout << (pic[i][j] ? 'X' : ' ');
cout << endl;
}
cout << "-\n";
}
return 0;
}
T4 Raid
思路:平面最近点对
先考虑平面最近点对的经典问题:给定平面内若干点的坐标,求任意两点之间距离的最小值。
若采用暴力枚举的做法,时间复杂度为\(O(n^2)\);利用分治,我们可以将其优化至\(O(n\log n)\).
我们将所有点按\(x\)坐标大小排序,将其按照\(x\)坐标大小分为两部分点,如图:
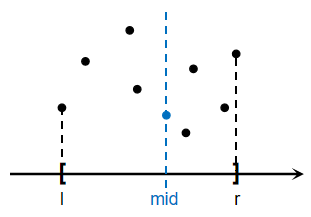
我们递的将点\([l,r]\)分为\([l,mid],[mid+1,r]\)两部分分别求最小值,再归的将\([l,mid],[mid+1,r]\)两部分的最小值合并为\([l,r]\)的最小值。
递的过程每层耗时\(O(1)\),我们主要讨论归的过程。
由于递的过程中我们已经得到了两部分点内部的最小值,所以在归的过程中,我们是在考虑两部分点之间的距离对答案产生的贡献。事实上,在归的过程中,能对答案造成贡献的点,一定不会距离\(x_{mid}\)特别远。假设我们现在拿到了子问题\([l,mid],[mid+1,r]\)的最小值\(d_1,d_2\),设\(d=\min\{d_1,d_2\}\),那么\(x\)坐标位于\([x_{mid}-d,x_{mid}+d]\)之外的点一定不会对答案做出任何贡献。假设左边的某点\(x<x_{mid}-d\),那么与右边任意一点的距离\(d'=\sqrt{(\Delta x)^2+(\Delta y)^2}\geqslant\Delta x\geqslant x_{mid}-x>d\).因此,我们只需要考虑\(x\in[x_{mid}-d,x_{mid}+d]\)之间的点即可。
\(\forall x\in[x_{mid}-d,x_{mid}+d]\),同样的,与点\(x\)距离小于\(d\)的点的纵坐标也不会离它太远,如图:
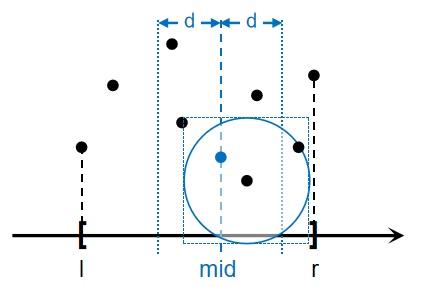
以点\(x\)为圆心,\(d\)为半径画圆,圆内的异侧点将对答案产生贡献(同侧点已经计算过)。为了简化判断,我们考虑所有\(y\in[x-d,x+d]\)的异侧点,并让点\(x\)与之更新。
合并过程总结如下:
- 求得子问题\([l,mid],[mid+1,r]\)的最小值\(d\)
- 考虑所有横坐标位于\([x_{mid}-d,x_{mid}+d]\)的点(设所有符合条件的点构成集合\(S\))
- \(\forall P(x,y)\in S\),将其与\(S\)中所有纵坐标位于\([x-d,x+d]\)的异侧点计算距离,更新答案
下证合并过程复杂度不超过\(O(6n)\).
只要证只有有限个点会与上述\(P\)进行距离的计算。特别地,有限点的个数不会超过6.
考虑极端情况,即点位于中线上,此时异侧部分所占面积最大,为正方形的一半。我们只要证相对于该点的异侧部分中,点的个数不会超过6.
根据我们对\(d\)的定义,同侧点的距离一定大于等于\(d\).为了利用这一性质,我们将这一区域分为6等分,如图:
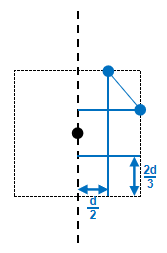
由抽屉原理知,当同侧存在多于6个点时,必然有两个位于同一个矩形中,它们的最远距离为对角线长\(d'=\sqrt{(\dfrac{d}{2})^2+(\dfrac{2d}{3})^2}=\dfrac{5d}{6}<d\),矛盾!
综上,分治的复杂度为\(O(n\log n)\).
在实现的过程中,由于我们每次需要快速找到与某一点纵坐标距离在\([x-d,x+d]\)的点,我们希望此时的点关于\(y\)也是有序的。又由于分治过程与归并排序的划分思路一致,我们可以利用归并排序,边做边对\(y\)归并,就能快速的找到这些点。
注:实际实现的时候,为了简洁起见,我们并没有严格区分同侧点与异侧点,而是将所有位于集合\(S\)中的点进行更新。从证明中可以看出,这样做并不会改变复杂度,而同侧点之间进行更新也不会对答案造成影响。
实现:
double ans;
struct Point {
int x, y;
bool operator<(const Point &b) const { return x < b.x; }
} p[N], tmp[N];
double dis(Point a, Point b) {
return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
double dfs(int l, int r) {
if (l == r)
return ans;
int mid = (l + r) >> 1;
int cnt = 0, mid_x = p[mid].x;
ans = min(dfs(l, mid), dfs(mid + 1, r)); // 3.
for (int pos = l, i = l, j = mid + 1; pos <= r; pos++) { // 归并
if (j > r || (i <= mid && p[i].y < p[j].y))
tmp[pos] = p[i++];
else
tmp[pos] = p[j++];
}
for (int pos = l; pos <= r; pos++)
p[pos] = tmp[pos];
for (int i = l; i <= r; i++) // 挑出[x_mid-d, x_mid+d]的点
if (abs(mid_x - p[i].x) < ans)
tmp[cnt++] = p[i];
for (int i = 0; i < cnt; i++)
for (int j = i - 1; j >= 0 && tmp[i].y - tmp[j].y < ans; j--) // 2.
ans = min(ans, dis(tmp[i], tmp[j]));
return ans;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> p[i].x >> p[i].y;
ans = dis(p[0], p[1]); // 1.
sort(p, p + n);
printf("%.3f\n", dfs(0, n - 1)); // 保留三位小数
return 0;
}
细节:
- 将初始距离指定为任意两点之间的距离,有效的缩小合并时考虑的\([x_{mid}-d,x_{mid}+d]\)的区间大小
- 将挑选出的点按照\((i,j)\ j<i\)的形式枚举点对,防止重复计算距离\((d(i,j)=d(j,i))\);此处为严格的小于号,否则当出现重合点时将出现问题
- 此处无需带着\(ans\)取\(\min\),由于递归过程中取\(\min\)时带有\(ans\),故\(dfs(l, mid), dfs(mid + 1, r)\leqslant ans\).
回到原题,题中具有两类点。与上述经典问题不同的是,经典问题采取的是几何距离\(d\),而本题我们需要定义相应的逻辑距离
将相同类型的点规定为无穷远,防止其对答案造成影响。在此基础上,我们对距离函数进行修改,然后直接套用上述做法。
也正因如此,经典问题中的一个重要性质消失了:当前问题中,同侧点的几何距离不一定大于等于\(d\).
当一堆同类的点聚在一起时,它们的距离将用\(\infty\)替代,这意味着合并过程中的同侧点可以包含若干几何距离小于\(d\)的同类点。按照上述做法,我们无法保证合并过程的复杂度为\(O(n)\),最坏情况下,甚至会退化至\(O(n^2)\),从而分治的复杂度变为\(O(n^2\log n)\).
我们能做的只有对它进行一定的优化,使复杂度不那么容易退化至恐怖的\(O(n^2\log n)\).
优化1:调整距离的定义
事实上,我们将同类点之间的距离设为\(\infty\)的目的是为了防止它更新答案。但将同类距离设为\(\infty\)会前功尽弃:在某一个合并支上,我们已经求出了当前的最小距离为\(d\),这意味着,当前合并支上,我们考虑的范围应包含于\([x_{mid}-d,x_{mid}+d]\).但倘若当前合并支左右两侧都是同类点的话,拿到的最小距离将是\(\infty\),从而会考虑全范围的点诱发复杂度退化。
从目的出发,既能防止答案更新、又能充分利用已有分支答案的做法是,当\(type_P=type_Q\)时,令\(D(P,Q)=d\).通过缩小考虑范围的规模,我们能对合并的复杂度进行一定的限制。
实现:
struct Point {
bool type = 0; // 类型标记
int x, y;
bool operator<(const Point &b) const { return x < b.x; }
} p[N], tmp[N];
double dis(Point a, Point b) {
return a.type == b.type ? ans : sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
// dfs内容同上
int main() {
int t, n;
cin >> t;
while (t--) {
cin >> n;
for (int i = 0; i < n; i++) // 两类点各n个
cin >> p[i].x >> p[i].y;
for (int i = n; i < n << 1; i++) {
cin >> p[i].x >> p[i].y;
p[i].type = 1;
}
ans = dis(p[0], p[(n << 1) - 1]); // 1.
sort(p, p + (n << 1));
printf("%.3f\n", dfs(0, (n << 1) - 1));
}
return 0;
}
细节:
- 排序前,点\(0,n-1\)一定为两个不同类型的点,选择点对\((0,n-1)\)的距离作为初始距离
优化2:旋转坐标系
从上述讨论我们发现,问题的关键在于同类点的混合。如果出题人构造了如下数据:
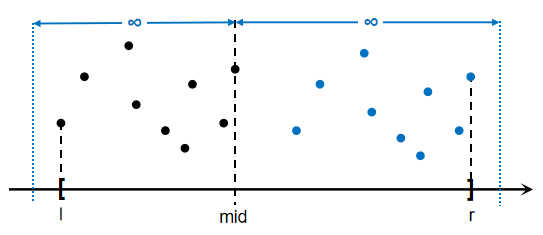
按照\(x\)坐标大小来划分,最后一次合并将是\(O(n^2)\)的。
如果我们按照斜线将点划分为两个区域,将让不同类的点适当混合,从而加快\(d\)缩小的进程。相对的来看,按照斜线划分点,等价于所有点的坐标进行旋转(绕原点),如图:
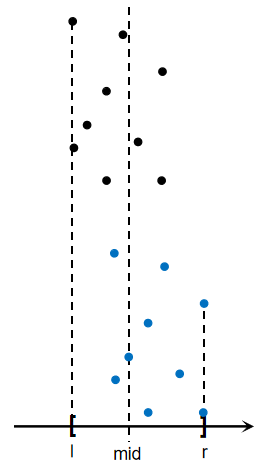
这样将有效解决不同类点混合的问题。
实现:
struct Point {
bool type = 0;
double x, y; // 旋转后出现小数
bool operator<(const Point &b) const { return x < b.x; }
} p[N], tmp[N];
// dis同上
double dfs(int l, int r) {
if (l == r)
return ans;
int mid = (l + r) >> 1;
int cnt = 0;
double mid_x = p[mid].x; // 此处mid_x同步改为double类型
ans = min(dfs(l, mid), dfs(mid + 1, r));
for (int pos = l, i = l, j = mid + 1; pos <= r; pos++) {
if (j > r || (i <= mid && p[i].y < p[j].y))
tmp[pos] = p[i++];
else
tmp[pos] = p[j++];
}
for (int pos = l; pos <= r; pos++)
p[pos] = tmp[pos];
for (int i = l; i <= r; i++)
if (abs(mid_x - p[i].x) < ans)
tmp[cnt++] = p[i];
for (int i = 0; i < cnt; i++)
for (int j = i - 1; j >= 0 && tmp[i].y - tmp[j].y < ans; j--)
ans = min(ans, dis(tmp[i], tmp[j]));
return ans;
}
int main() {
int t, n, x, y;
double theta;
srand(time(0));
cin >> t;
while (t--) {
theta = rand() % 360;
theta = theta / 180 * acos(-1);
cin >> n;
for (int i = 0; i < n; i++) {
cin >> x >> y;
p[i].x = x * cos(theta) - y * sin(theta);
p[i].y = x * sin(theta) + y * cos(theta);
}
for (int i = n; i < n << 1; i++) {
cin >> x >> y;
p[i].x = x * cos(theta) - y * sin(theta);
p[i].y = x * sin(theta) + y * cos(theta);
p[i].type = 1;
}
ans = dis(p[0], p[(n << 1) - 1]);
sort(p, p + (n << 1));
printf("%.3f\n", dfs(0, (n << 1) - 1));
}
return 0;
}
优化3:打乱相同横坐标
旋转的策略能有效解决大部分同类点的混合,但当点分布在转轴上时将束手无策,如图:
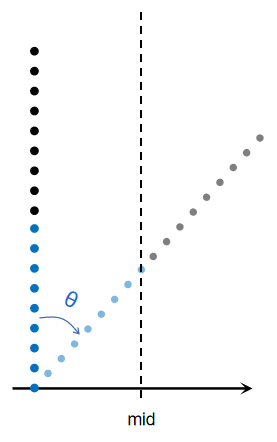
可以看到,无论怎样旋转,所有同类点仍将混合在一起。
我们采取这样的策略:当点的横坐标相等时,将这些点打乱。这样数组内部点的实际顺序就变得与直观看见的不同了:
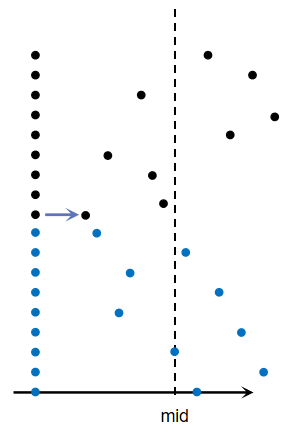
尽管这些点的横坐标相同,但在数组中的实际顺序决定了按照上述做法能有效的将不同类的点进行混合。
为了实现随机打乱,我们为每个点附加一个随机数,并将其作为第二关键字参与排序。
实现:
struct Point {
bool type = 0;
int x, y, rd = rand();
bool operator<(const Point &b) const {
return x == b.x ? rd < b.rd : x < b.x;
}
} p[N], tmp[N];
// dis同上
double dfs(int l, int r) {
if (l == r)
return ans;
int mid = (l + r) >> 1;
int cnt = 0, mid_x = p[mid].x;
ans = min(dfs(l, mid), dfs(mid + 1, r));
for (int pos = l, i = l, j = mid + 1; pos <= r; pos++) {
if (j > r || (i <= mid && p[i].y < p[j].y))
tmp[pos] = p[i++];
else
tmp[pos] = p[j++];
}
for (int pos = l; pos <= r; pos++)
p[pos] = tmp[pos];
for (int i = l; i <= r; i++)
if (abs(mid_x - p[i].x) < ans)
tmp[cnt++] = p[i];
for (int i = 0; i < cnt; i++)
for (int j = i - 1; j >= 0 && tmp[i].y - tmp[j].y < ans; j--)
ans = min(ans, dis(tmp[i], tmp[j]));
return ans;
}
int main() {
int t, n, x, y;
cin >> t;
srand(time(0));
while (t--) {
cin >> n;
for (int i = 0; i < n; i++)
cin >> p[i].x >> p[i].y;
for (int i = n; i < n << 1; i++) {
cin >> p[i].x >> p[i].y;
p[i].type = 1;
}
ans = dis(p[0], p[(n << 1) - 1]);
sort(p, p + (n << 1));
printf("%.3f\n", dfs(0, (n << 1) - 1));
}
return 0;
}
T5 防线
思路:二分+前缀和
本题有一个十分重要的性质:奇数点至多只有一个。
我们用\(0\)来代表偶数,\(1\)来代表奇数,问题转化为在\(01\)序列中寻找至多只有一个的\(1\).例如序列\(00010000\),我们的目标是找到3号位的\(1\)(下标从0开始)。
由于序列长\(m\)上限\(2^{31}\),我们需要一个\(O(n\log m)\)的算法。因此,我们需要在序列上二分。
回顾二分的本质:寻找边界值。为此,我们期望构造出类似\(00011111\)的序列,这样我们可以利用二分顺利的找到边界。
形式上,这类似于原\(01\)序列的前缀和。而由于奇数与偶数的和仍为奇数、偶数与偶数的和仍为偶数,所以我们可以将原序列中的每个数定义为序列起点到序列终点的防具之和的奇偶性,奇数为\(1\),偶数为\(0\).
现在我们的问题转化为求某一段序列\([x,y]\)的防具之和。更一般的,我们考虑求\([0,x]\)的防具之和\(S(x)\),那么\([x,y]\)的防具之和为\(S(y)-S(x-1)\).
注:求\(S(x)\)而不是直接求\(S(x,y)\)的好处在于原点始终位于所有左端点的左侧(或重合)
考虑每一类防具\(i\),\(S(x)=\sum\limits_{i=1}^nS_i(x)\),我们只需要求出该类防具在\([0,x]\)上摆放的防具数\(S_i(x)\)即可。
当\(s_i>x\)时,\(i\)类防具的起点落在了整个考察区间的外面,没有任何防具落在区间内,贡献为0.
当\(s_i\leqslant x\)时,应考虑相应的终点\(e=\min\{e_i,x\}\).则落在区间内的防具数量为\(\lfloor\dfrac{e}{d_i}\rfloor+1\),如图:
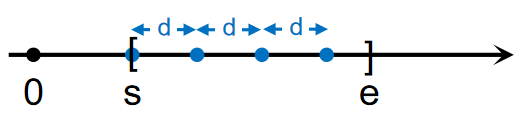
综上,
实现:
struct Armor {
int s, e, d;
} a[N];
int n, l, _l, r;
int getSum(int x) {
int res = 0;
for (int i = 0; i < n; i++) {
if (a[i].s > x)
continue;
res += (min(a[i].e, x) - a[i].s) / a[i].d + 1;
}
return res;
}
bool check(int x) { return (getSum(x) - getSum(_l - 1)) % 2; }
int main() {
int t, mid;
cin >> t;
while (t--) {
cin >> n;
l = INF, r = -1;
for (int i = 0; i < n; i++) {
cin >> a[i].s >> a[i].e >> a[i].d;
a[i].e = (a[i].e - a[i].s) / a[i].d * a[i].d + a[i].s; // 将e移至最后一个防具处
l = min(l, a[i].s), r = max(r, a[i].e);
}
_l = l; // 防具起点
while (l < r) {
mid = ((long long)l + r) >> 1; // l=1,r=INT_MAX时可能溢出,需强制类型转换
if (check(mid))
r = mid;
else
l = mid + 1;
}
if (check(l)) { // INT_MAX+1溢出,故采取二次检查的方式判断无解情况,而不是将初始区间设为[0,_r+1]
cout << l << ' ' << getSum(l) - getSum(l - 1) << endl;
} else
cout << "There's no weakness." << endl;
}
return 0;
}
T6 Corral the Cows
思路:二分+离散化+前缀和
寻找最小畜栏属于最优化问题,我们对畜栏长度进行二分。
为了快速求出某区域内三叶草总量,我们需要处理三叶草数量的二维前缀和。
注意到三叶草数小于等于500,而坐标取值最大为10000,我们考虑对坐标进行离散化。离散化要求问题求解应依赖于数据的相对大小,而本题中恰好有这样的性质:考虑当前有两株三叶草,分别位于\((0,0),(500,500)\),当我们框定\((0,0)\sim(n,n)\ n<500\)的范围时,都将得到唯一的一株三叶草,换句话说,只有当坐标的相对大小改变了,才会对答案产生贡献。故此处可以使用离散化。
现在问题转化为判定,即在离散化后的数组中确定当前给定畜栏长度最多能覆盖多少三叶草。
我们将利用二维前缀和求出最终的答案,故问题转化为确定离散化后的坐标\((x_1,y_1),(x_2,y_2)\),使得它代表的离散化前的区域\((x[x_1],y[y_1]),(x[x_2],y[y_2])\)满足给定的畜栏长度\(len\).
先考虑\(x\)方向。我们先枚举其中一个点,那么另一个点受\(len\)的限制而随之确定。不妨先枚举\(x_2\)(\(x_2>x_1\)).
当\(len\)过大时,即\(len\)能过将所有的离散化前的\(x\)覆盖住(\(len>x[x_2]-x[1]+1\)),那么我们只需要考虑\(x[x_2]=\max x\)的情形:此时所有的\(x\)都被\(len\)覆盖住,为能够达到的最大覆盖。
注:此处涉及前缀和,数组下标从1开始
当\(len\)不能将所有\(x\)覆盖住时,我们应该寻找\(x_1\ s.t.x[x_2]-x[x_1]+1\leqslant len,x[x_2]-x[x_1-1]+1>len\),即构成\(\leqslant len\)的最大距离。由于前面我们已经说过,最终的答案只与\(x\)的相对大小有关,当\(x[x_2]-x[x_1]+1\not=len\)时,就算将\(x[x_1]\)移动至\(x[x_2]-len+1\)处,也不会对答案造成任何贡献,如图:
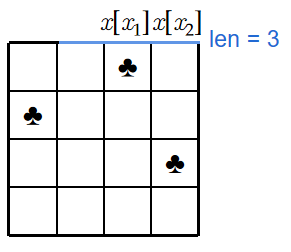
在枚举\(x_1,x_2\)的基础上,按照同样的方式枚举\(y_1,y_2\)即可确定我们所要的离散化后的坐标\((x_1,y_1),(x_2,y_2)\).
实现:
const int N = 500 + 5, INF = 1e4 + 5;
int _x[N], _y[N], x[N], y[N], c, s[N][N], cntx, cnty;
// _x[],_y[]存储原始数据,x[],y[]为离散化数组,cntx,cnty为离散化后值的个数
int query(int a[], int n, int x) {
return lower_bound(a + 1, a + n + 1, x) - a; // 数组下标从1开始
}
bool check(int len) {
for (int x2 = 1, x1 = 1; x2 <= cntx; x2++)
if (x[x2] - x[1] + 1 >= len || x2 == cntx) { // len过大时只考虑x_max即x[xcnt]
while (x[x2] - x[x1] + 1 > len)
x1++;
for (int y2 = 1, y1 = 1; y2 <= cnty; y2++)
if (y[y2] - y[1] + 1 >= len || y2 == cnty) {
while (y[y2] - y[y1] + 1 > len)
y1++;
if (s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] >=
c)
return true;
}
}
return false;
}
int main() {
int n;
cin >> c >> n;
for (int i = 1; i <= n; i++) {
cin >> _x[i] >> _y[i];
x[i] = _x[i], y[i] = _y[i];
}
sort(x + 1, x + 1 + n); // 对x,y分别离散化
sort(y + 1, y + 1 + n);
cntx = unique(x + 1, x + n + 1) - (x + 1);
cnty = unique(y + 1, y + n + 1) - (y + 1);
for (int i = 1; i <= n; i++)
s[query(x, cntx, _x[i])][query(y, cnty, _y[i])]++;
for (int i = 1; i <= cntx; i++) // 求离散化后的二维前缀和
for (int j = 1; j <= cnty; j++)
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + s[i][j];
int l = 1, r = INF;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid))
r = mid;
else
l = mid + 1;
}
cout << l << endl;
return 0;
}
T7 糖果传递
思路:中位数
环形均分纸牌原题,弱化版七夕祭。
实现:
long long a[N], avg, sum, pos, ans;
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
sum += a[i];
}
avg = sum / n;
for (int i = 0; i < n; i++)
a[i] -= avg;
for (int i = 1; i < n; i++)
a[i] += a[i - 1];
sort(a, a + n);
pos = a[(n - 1) >> 1]; // 数组下标从0开始
for (int i = 0; i < n; i++)
ans += abs(a[i] - pos);
cout << ans << endl;
return 0;
}
T8 Soldiers
思路:中位数
\(x,y\)方向独立。\(y\)方向为货仓选址问题,我们主要看\(x\)方向的处理。
最终的目的是将所有的\(x\)移动至相邻的状态。相邻意味着一旦其中的某一点的位置确定,那么所有点的位置将被确定。
首先有这样一个性质:所有点横坐标的相对大小不会改变。否则,一旦出现交叉,如图:
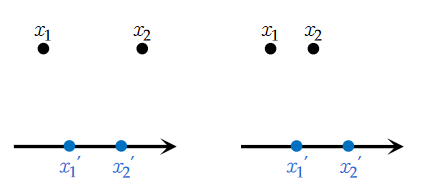
当两个点都向内移动时,如左图,不交叉的移动距离\(d=|x_1-x_1'|+|x_2-x_2'|\),交叉移动距离\(d'=|x_1-x_2'|+|x_2-x_1'|=d+2|x_1'-x_2'|>d\).
当至少有一个点向外移动时,如右图,不妨设\(x_2\)移动至外部,则交叉移动距离与不交叉移动距离差为 $$ d'-d=|x_1-x_2'|+|x_2-x_1'|-(|x_1-x_1'|+|x_2-x_2'|)\ =(|x_1-x_2'|-|x_2-x_2'|)+(|x_2-x_1'|-|x_1-x_1'|)\ =(|x_1-x_2|+|x_2-x_1'|)-|x_1-x_1'|\
|x_1-x_1'|-|x_1-x_1'|=0 $$ 综上,所有点横坐标的相对大小不会改变。故先将\(x\)排序。
按照这样的思路,我们将最终位置看作相对位移+绝对位移,即\(x_i\)应移动至\(i+k\)处(横坐标相对大小不变)。问题转化为求 $$ \min\sum\limits_{i=1}^n|x_i-(i+k)|=\min\sum\limits_{i=1}^n|(x_i-i)-k| $$ 我们将\(x_i-i\)看作一个整体\(z_i\),故问题转化为在\(\{z_n\}\)上做货舱选址,即\(k\)为\(\{z_n\}\)中位数。
实现:
sort(x, x + n);
sort(y, y + n);
for (int i = 0; i < n; i++)
x[i] -= i;
sort(x, x + n);
posx = x[(n - 1) >> 1], posy = y[(n - 1) >> 1];
for (int i = 0; i < n; i++)
ans += abs(x[i] - posx) + abs(y[i] - posy);
T9 Number Base Conversion
思路:进制转换+高精
将原数制\(k\)转化为10进制:\(n_{k}=\overline{a_n\cdots a_1a_0},n_{10}=\sum\limits_{i=0}^n a_ik^i\)
将10进制转化为目标数制:短除法
高精:
struct number {
int len;
vector<int> n;
number &operator=(const char *);
number &operator=(int);
number();
number(int);
bool operator<(const number &) const;
bool operator!=(const number &) const;
number operator+(const int &) const;
number operator*(const number &) const;
number operator/(const int &) const;
int operator%(const int &) const;
number &operator/=(const int &);
};
number &number::operator=(const char *c) {
n.clear();
len = 1;
int l = strlen(c), k = 1, tmp = 0;
for (int i = 1; i <= l; i++) {
if (k == 10000) {
n.push_back(tmp);
len++, k = 1, tmp = 0;
}
tmp += k * (c[l - i] - '0');
k *= 10;
}
n.push_back(tmp);
return *this;
}
number &number::operator=(int a) {
char s[15];
sprintf(s, "%d", a);
return *this = s;
}
number::number() {
n.clear();
n.push_back(0);
len = 1;
}
number::number(int n) { *this = n; }
bool number::operator<(const number &b) const {
if (len != b.len)
return len < b.len;
for (int i = len - 1; i >= 0; i--)
if (n[i] != b.n[i])
return n[i] < b.n[i];
return false;
}
bool number::operator!=(const number &b) const {
return (b < *this) || (*this < b);
}
number number::operator+(const int &b) const {
number c;
c.len = len;
for (int i = 0; i < c.len; i++)
c.n.push_back(n[i]);
c.n.push_back(0);
c.n[0] += b;
int cnt = 0;
while (c.n[cnt] >= 10000) {
c.n[cnt] -= 10000, c.n[++cnt]++;
}
if (c.n[c.len])
c.len++;
else
c.n.pop_back();
return c;
}
number number::operator*(const number &b) const {
number c;
c.len = len + b.len + 1;
for (int i = 0; i < c.len; i++)
c.n.push_back(0);
for (int i = 0; i < len; i++)
for (int j = 0; j < b.len; j++) {
c.n[i + j] += n[i] * b.n[j];
c.n[i + j + 1] += c.n[i + j] / 10000;
c.n[i + j] %= 10000;
}
while (c.n[c.len - 1] == 0 && c.len > 1) {
c.len--;
c.n.pop_back();
}
return c;
}
number number::operator/(const int &b) const {
long long tmp = 0;
number c;
c.len = len;
for (int i = 0; i < c.len; i++)
c.n.push_back(0);
for (int i = len - 1; i >= 0; i--) {
tmp = tmp * 10000 + n[i];
c.n[i] = tmp / b;
tmp %= b;
}
while (c.n[c.len - 1] == 0 && c.len > 1) {
c.len--;
c.n.pop_back();
}
return c;
}
int number::operator%(const int &b) const {
long long tmp = 0;
number c;
c.len = len;
for (int i = 0; i < c.len; i++)
c.n.push_back(0);
for (int i = len - 1; i >= 0; i--) {
tmp = tmp * 10000 + n[i];
c.n[i] = tmp / b;
tmp %= b;
}
return tmp;
}
number &number::operator/=(const int &b) { return *this = *this / b; }
算法主体:
int char_to_num(char a) {
if ('0' <= a && a <= '9')
return a - '0';
if ('A' <= a && a <= 'Z')
return a - 'A' + 10;
return a - 'a' + 36;
}
char num_to_char(int n) {
if (0 <= n && n <= 9)
return n + '0';
if (10 <= n && n <= 35)
return n - 10 + 'A';
return n - 36 + 'a';
}
int main() {
int t, from, to;
string ori, ans;
number n;
cin >> t;
while (t--) {
n = 0, ans = "";
cin >> from >> to >> ori;
cout << from << ' ' << ori << endl << to << ' ';
if (ori == "0") {
cout << 0 << endl << endl;
continue;
}
for (int i = 0; i < ori.length(); i++)
n = n * (number)from + char_to_num(ori[i]);
while (n != (number)0) {
ans += num_to_char(n % to); // C++风格字符串支持string+char
n /= to;
}
for (int i = ans.length() - 1; i >= 0; i--)
cout << ans[i];
cout << endl << endl;
}
return 0;
}
T10 Cow Acrobats
思路:微扰
用微扰来确认牛的排序标准。交换牛\(k,k+1\)并不会对其余的牛造成影响,且牛\(k,k+1\)的交换有效,当且仅当
又\(w>0\),故\(-s_k<w_{k+1}-s_k,w_k-s_{k+1}>-s_{k+1}\).所以 $$ w_k-s_{k+1}>w_{k+1}-s_k>-s_k $$ 即\(w_k+s_k>w_{k+1}+s_{k+1}\).故排序标准为\(w+k\),升序排列。
实现:
pair<int, pair<int, int>> cow[N];
int main() {
int n, ans = -INF, sum = 0; // 1.
cin >> n;
for (int i = 0; i < n; i++) {
cin >> cow[i].second.first >> cow[i].second.second;
cow[i].first = cow[i].second.first + cow[i].second.second;
}
sort(cow, cow + n);
for (int i = 0; i < n; i++) {
ans = max(ans, sum - cow[i].second.second);
sum += cow[i].second.first;
}
cout << ans << endl;
return 0;
}
细节:
- ans需初始化为\(-\infty\),\(\sum w-s\)最大值可能为负
T11 To the Max
思路:前缀和+贪心
按照常规做法,我们处理出原矩阵的二维前缀和,然后暴力枚举\(x_1,x_2,y_1,y_2\),复杂度\(O(n^4)\).
事实上,我们可以将复杂度优化至\(O(n^3)\).
换一个枚举方式,我们枚举上下边界,即\(y_1,y_2\),然后计算\(y_1,y_2\)间最大的子块,如图:
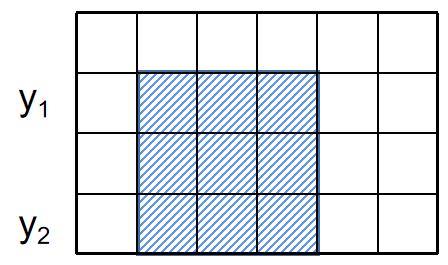
让我们先考虑一下它的一维版本,即序列最大连续和。
我们从\(a_1\)开始依次向后考虑,并设当前最大和为\(sum\),已考虑前\(k-1\)项。对于第\(k\)项,我们采取如下的贪心策略(记作\(A\)):
- 若\(sum\leqslant 0\),则丢弃\(sum\)原有值,令\(sum=a_k\)
- 若\(sum>0\),则将\(a_k\)放入\(sum\)中,令\(sum=sum+a_k\)
假设存在更优策略\(O\),对于第一条,\(sum_O=sum+a_k\leqslant a_k=sum_A\);对于第二条,\(sum_O=a_k<sum+a_k=sum_A\),矛盾!
故贪心正确性得证。
现在,我们将它拓展至高维。为了快速获得\(\sum\limits_{y=y_1}^{y_2}a_{x,y}\)的值,我们需要对每一列处理前缀和,即 $$ s_{i,j}=\sum\limits_{y=1}^ja_{i,y} $$ 这样,我们便可以在\(O(n^3)\)的复杂度下求解原问题。
实现:
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
cin >> s[i][j];
s[i][j] += s[i - 1][j];
}
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j++) {
sum = 0;
for (int k = 1; k <= n; k++) {
if (sum <= 0)
sum = s[j][k] - s[i - 1][k];
else
sum += s[j][k] - s[i - 1][k];
ans = max(ans, sum);
}
}
T12 Task
思路:贪心
贪心策略:选择当前\(x\)最大的任务,将它安排在可安排的\(y\)最小的机器上。
证明:
由于\(y\in[0,100]\),\(y\)的波动对答案造成的影响\(\leqslant 200<500\),故我们优先考虑\(x\).
其次,题目要求我们在保证任务完成最多的前提下考虑收入最大,所以我们考虑的顺序是:完成的任务数、\(x,y\).
记原策略为\(A\),设\(O_1\)为选择当前\(x\)次大的任务。
对于任务数,若放完最大任务后,仍可以放入次大任务,则\(sub_A+w_A=sub_{O_1}+w_{O_1}+1>sub_{O_1}+w_{O_1}\);若放完最大任务后,无法放入次大任务,则\(sub_A+w_A=sub_{O_1}+w_{O_1}\),故\(sub_A+w_A\geqslant sub_{O_1}+w_{O_1}\).
对于\(x\),由于\(x_{最大任务}>x_{次大任务}\),所以\(w_A>w_{O_1}\),进而\(sub_A+w_A>sub_{O_1}+w_{O_1}\).
故策略\(O_1\)并不优于\(A\).
设\(O_2\)为将\(x\)最大的任务安排在可安排的\(y\)次小的机器上。
对于任务数,放到\(y\)最小的机器后,若\(y\)次小的机器能容纳下一个任务,\(sub_A+w_A=sub_{O_2}+w_{O_2}+1>sub_{O_2}+w_{O_2}\);若不能,则\(sub_A+w_A=sub_{O_2}+w_{O_2}\),故\(sub_A+w_A\geqslant sub_{O_2}+w_{O_2}\).
对于\(y\),对于同一个任务,\(y\)的贡献与机器无关,故\(sub_A+w_A=sub_{O_2}+w_{O_2}\).
故策略\(O_2\)并不优于\(A\).即证。
现在的问题是快速找到某任务可被安排的\(y\)最小的机器。我们可以每次将能容纳新任务的机器加入multiset中,由于\(x\)递减,故上次剩余的机器仍能被下一个任务使用。我们利用lower_bound寻找具有最小\(y\geqslant y_i\)的机器,并在统计答案后将其删去。
实现:
pair<int, int> work[N], machine[N];
multiset<int> s;
int main() {
int n, m, cnt, ans;
long long w;
while (cin >> n >> m) {
ans = w = 0;
for (int i = 0; i < n; i++)
cin >> machine[i].first >> machine[i].second;
for (int i = 0; i < m; i++)
cin >> work[i].first >> work[i].second;
sort(machine, machine + n, greater<pair<int, int>>()); // 递减
sort(work, work + m, greater<pair<int, int>>());
cnt = 0;
for (int i = 0; i < m; i++) {
while (cnt < n && machine[cnt].first >= work[i].first)
s.insert(machine[cnt++].second);
auto it = s.lower_bound(work[i].second); // 返回迭代器
if (it != s.end()) { // it == s.end()时查找失败,即没有可以容纳该任务的机器
ans++, w += 500 * work[i].first + 2 * work[i].second;
s.erase(it);
}
}
cout << ans << ' ' << w << endl;
}
return 0;
}