前缀和与差分

前缀和

定义：\(S_n=\sum\limits_{i=1}^n a_i\)

应用：求部分和

\(sum(l,r)=\sum\limits_{i=l}^ra_i=S_r-S_{l-1}\)

\(O(n)\)预处理前缀和，\(O(1)\)查询部分和

---

例1激光炸弹

思路：二维前缀和

即要求最大的二维部分和，故可以先预处理出二维前缀和，再遍历所有的二维部分和。

先求二维前缀和，记\(S_{m,n}=\sum\limits_{i=1}^m\sum\limits_{j=1}^na_{i,j}\).

仿照一维前缀和，我们有\(a_n=S_n-S_{n-1}\Leftrightarrow S_n=S_{n-1}+a_n\),利用递推初始化\(S_n\);类似的，我们可以利用递推初始化\(S_{m,n}\),即寻找\(S_{m,n}\)与\(S_{m-1,n},S_{m,n-1},S_{m,n},a_{m,n}\)之间的关系，如下图所示：

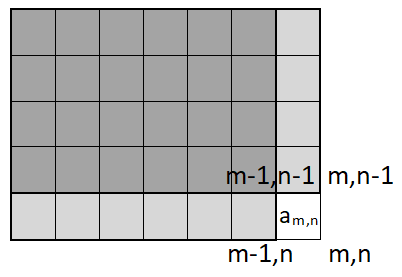
写作数学表达式即为：

\(S_{m,n}=S_{m-1,n}+S_{m,n-1}-S_{m-1,n-1}+a_{m,n}\),需\(O(m*n)\)时间完成初始化。

再利用二维前缀和求二维部分和，利用部分和区域的四个顶点，如下图所示：

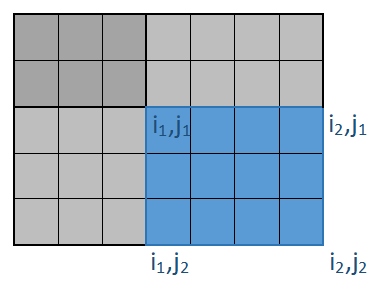
写作数学表达式即为：

\(\sum\limits_{i=i_1}^{i_2}\sum\limits_{j=j_1}^{j_2}a_{i,j}=S_{i_2,j_2}-S_{i_2,j_1-1}-S_{i_1-1,j_2}+S_{i_1-1,j_1-1}\ (*)\)

回到本题，我们假设爆炸范围右下角坐标为\((i,j)\),那么左上角坐标为\((i-R+1,j-R+1)\),如图：

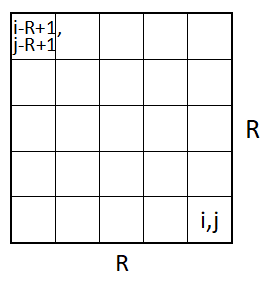
代入\((*)\)得：

\(sum(i,j)=S_{i,j}-S_{i,j-R}-S_{i-R,j}+S_{i-R,j-R}\)

这里有一个细节需要注意，即题中所给\((X_i,Y_i)\)为格点坐标而非格子。我们可以将其视为坐标为\((X_i,Y_i)\)格子的中点，而爆炸边界位于格子边线，如图：

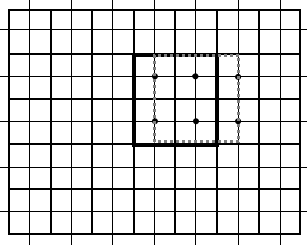
此时(黑色边界)能容纳的格点数最多；反之，若选择格点边线做爆炸边界(灰色边界)，则因边界上目标不会被摧毁而使容纳量降低。

此时将格点视作其所在的格子，即转化为上述分析所对应的情形。

实现：

#include <bits/stdc++.h>
using namespace std;
const int N = 5e3 + 5;
int s[N][N];
int main() {
  int n, r, x, y, w, max_x = 0, max_y = 0, ans = -1;
  cin >> n >> r;
  r = min(r, 5001); // 特判全覆盖；0化为1，5000化为5001
  for (int i = 0; i < n; i++) {
    cin >> x >> y >> w;
    s[x + 1][y + 1] += w; // 坐标从0开始
    max_x = max(max_x, x + 1), max_y = max(max_y, y + 1);
  }
  max_x = max(max_x, r), max_y = max(max_y, r); // 1.
  for (int i = 1; i <= max_x; i++)
    for (int j = 1; j <= max_y; j++)
      s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + s[i][j]; // 2.
  for (int i = r; i <= max_x; i++)
    for (int j = r; j <= max_y; j++)
      ans = max(ans, s[i][j] - s[i][j - r] - s[i - r][j] + s[i - r][j - r]);
  cout << ans << endl;
  return 0;
}

细节：

1.前缀和计算范围：先考虑上界：

(1)包含所有有点区域，即\(x\geqslant\max X_i,y\geqslant\max Y_i\).(2)满足贴边的爆炸区域，即\(x,y\geqslant R\),如下图所示：

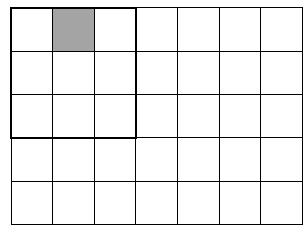
当\(\max X_i\leqslant R\)时，在x方向上为了尽可能的纳入更多的格子，爆炸范围应贴边摆放；此时应保证贴边时右下角的前缀和完成初始化，否则无法得到正确的结果。

当\(max X_i>R\)时，在x方向上为了不纳入空白格子，爆炸范围下边界不会超出\(max X_i\).

再考虑下界：

由\(S_{1,1}=a_{1,1}\),故此时仅\(S_{1,1}\)完成初始化，而\(S_{1,j},S_{i,1}\)并未完成，故需从\((1,1)\)开始初始化。

综上，前缀和计算范围为\(\left\{\begin{array}{ll}1\leqslant x\leqslant \max X_i,\\1\leqslant y\leqslant\max Y_i\end{array}\right.\)

2.此题所给空间不够两个数组，故将\(a_{i,j}\)直接存在\(S_{i,j}\)中，由于前缀和计算时右边到左边\(i,j\)递增，故可保证\(a_{i,j}\)不会被提前抹去，且\(S_{i,j}\)计算顺序准确，从而可得到正确的\(S_{i,j}\).

差分

定义：\(b_1=a_1,b_i=a_i-a_{i-1}(2\leqslant i\leqslant n)\)

性质：与前缀和互为逆运算

略证：\(\Delta_{S_i}=S_i-S_{i-1}=a_i,\sum\limits_{i=1}^n\Delta_i=a_1+\sum\limits_{i=2}^n(a_i-a_{i-1})=a_1+a_n-a_1=a_n\)

应用：将原序列上的区间操作转化为差分序列上的单点操作，即\(a_{i..j}+d\Leftrightarrow \Delta_i+d,\Delta_{j+1}-d\)

略证：

对于\(\Delta_{1..i-1}\),由于\(a_{1..i-1}\)不变，无影响；

对于\(\Delta_i\),由于\(a_i+d\)而\(a_{i-1}\)不变，故\(\Delta_i+d\)；

对于\(\Delta_{i+1..j}\),由于\(a_{i..j}+d\)，故\(\Delta_{i+1..j}\)不变;

对于\(\Delta_{j+1}\),由于\(a_j+d\)而\(a_{j+1}\)不变，故\(\Delta_{j+1}-d\)

特别的，当j=n时，此时\(\Delta_{n+1}\)无意义，可设为任意值

---

例2 IncDec Sequence

思路：差分

容易想到将区间操作转化为单点操作。题中操作即转化为选择差分序列中的两个数，一个加一，一个减一，使得\(\Delta_{2..n}=0\).

由于题目条件要求操作次数最少，故优先在\(\Delta_{2..n}\)中操作。设其中正数之和为\(p\)，负数之和为\(-q\)，两两配对并操作至无法配对，共操作\(\min\{p,q\}\)次。

接着处理\(\Delta_{2..n}\)中剩余非0项。一方面，我们可以利用\(\Delta_1\),它不在目标要求之中；另一方面，我们可以利用\(\Delta_{n+1}\),它没有定义，可任意设值。因此，我们可以将剩余非零项与\(\Delta_1,\Delta_{n+1}\)配对并使之归零，需操作\(|p-q|\)次。

综上，至少操作\(min\{p,q\}+|p,q|=max\{p,q\}\)次。

值得注意的是，我们不会将\(\Delta_1,\Delta_{n+1}\)配对，它对目标达成无任何贡献；从区间操作的角度来看，相当于将\(a_{1..n}\)同时变化，显然无效。

换言之，中间的数受到其左右两边数大小的限制，而首尾两数只受其一边数大小的限制，我们先处理限制强的，再利用限制松的进行调整。

再考虑最终数列的种数。导致答案出现多解的根源在于处理\(\Delta_{2..n}\)中剩余非0项时利用\(\Delta_1,\Delta_{n+1}\)情况不同。因此，解的个数即为将\(|p-q|\)拆成两数的组数，为\(|p-q|+1\)组。

实现：

cin >> n >> pre;
for (int i = 1; i < n; i++) {
  cin >> cur;
  d = cur - pre; // 差分值仅取决与前驱值和当前值，可使用两个变量节省空间
  d > 0 ? p += d : q -= d;
  pre = cur;
}
cout << max(p, q) << endl; 
cout << abs(p - q) + 1 << endl;

例3 Tallest Cow

思路：差分

先证任意区间不会交叉，否则对于编号为\(a,b,c,d\)的4头牛(其中\(a<b<c<d\))且\(a,c\)与\(b,d\)互相看见，由\(b,d\)互相看见\(\Rightarrow c<b\),与\(b<c\)矛盾！所以不存在交叉区间。

我们可以将牛的初始高度看作等高(为0)，然后通过降低部分牛的身高使其满足条件。

对于第一组关系，为了使\(A,B\)能互相看见，我们将\(A,B\)中间的所有牛身高降低一格，为这些牛的最高身高，如图：

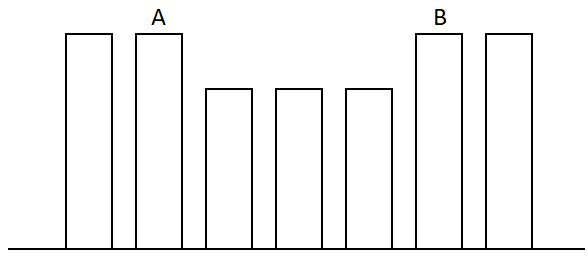
由于我们已经证明了任意两个区间不会交叉，故与\(A,B\)有关的区间与\(A,B\)形成嵌套关系。

若\(A',B'\)在\(A,B\)内，直接将\(A',B'\)间的牛身高降低一格，如图：

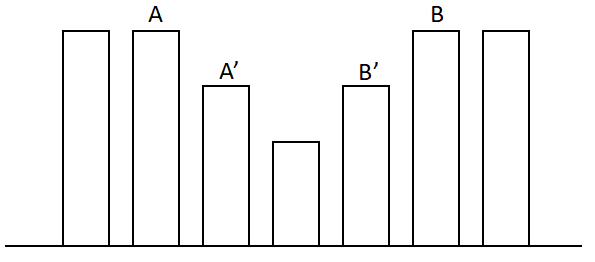
这样既满足了\(A',B'\)的要求，又满足了\(A,B\)的要求。

若\(A',B'\)在\(A,B\)内，类似的，将\(A',B'\)间的牛身高降低一格，如图：

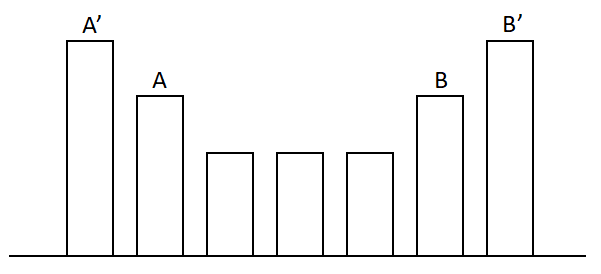
若我们只降低\(A,B\)的高度，而不降低\(A,B\)中间的高度，尽管\(A',B'\)的关系得到满足，但\(A,B\)关系被破坏，原因在于\(A..B\)构成一个满足条件的整体，只修改\(A..B\)的端点会破坏该整体，从而使\(A，B\)不再满足条件；反过来，将它们全部降低，此时\(A..B\)作为整体整体降低一格，关系得到保留。

对于区间操作，容易想到用差分降低时间复杂度；我们可以维护奶牛身高数列的差分数列，每次降低身高时在区间端点进行操作，最后再求前缀和还原出奶牛的身高。

实现：

for (int i = 0; i < m; i++) {
  cin >> A >> B;
  if (A > B) // 保证A..B中A<B
    swap(A, B);
  if (!vis[A][B]) // 去重
    b[A + 1]--, b[B]++, vis[A][B] = 1; // 1.
}
for (int i = 1; i <= n; i++) {
  s += b[i];
  cout << s + h << endl; // 2.
}

细节：

1.此处用差分维护区间操作：将\(A+1..B-1\)全部减一，等价于\(\Delta_{A+1}-1,\Delta_B+1\)

2.由于不会有跨过最高牛的区间，故前缀和还原后的数列中最高牛对应高度为0，所以需将所有牛加上高度H得到真正的最大高度