二分¶
应用:当问题的答案具有单调性时,可以通过二分把求解转化为判定
复杂度理论:判定难度小于求解
效率提升本质:利用单调性,通过一次比较即可批量判断解是否符合条件
整数集合上的二分¶
规定:
1.答案位于\([l,r]\)中
注:\([l,r]\)为当前能确认含有答案的准确区间,即\(l,r\)符合条件,而\(l-1,r+1\)不符合条件
2.每次循环后区间缩小
3.条件为\(mid\)符合条件
分类:
a.若\(mid\)符合条件,则区间向左缩小,如图:
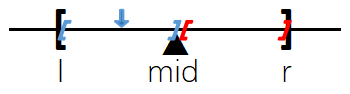
由1知,当\(mid\)符合条件时,\([l,r]\rightarrow[l,mid]\);当\(mid\)不符合条件时,\([l,r]\rightarrow[mid+1,r]\)
由2知,\(\left\{\begin{array}{ll}mid<r,\\mid+1>l\end{array}\right.\Leftrightarrow l-1<mid<r\)
由于我们要进行二分操作,\(mid\)应尽量与\(\dfrac{l+r}{2}\)靠近,又由于\(mid\in \mathbb{Z}\),故问题转化为选择\(\lfloor\dfrac{l+r}{2}\rfloor\)还是\(\lceil\dfrac{l+r}{2}\rceil\)作为\(mid\)的值。
易知\(x-1<\lfloor x\rfloor\leqslant x\),故选择\(mid=\lfloor\dfrac{l+r}{2}\rfloor\)时有\(\dfrac{l+r}{2}-1<mid\leqslant\dfrac{l+r}{2}\),
由1知,\(l<r\),故\(mid>\dfrac{l+r}{2}-1>\dfrac{l+l}{2}-1=l-1,mid\leqslant\dfrac{l+r}{2}<\dfrac{r+r}{2}=r\),
即\(l-1<mid<r\),符合条件。
实现:
细节:
1.终止时\(l=r\),则\(l\leqslant ans\leqslant r=l\Leftrightarrow ans=l=r\)
2.\(\lfloor\dfrac{l+r}{2}\rfloor\)应写作(l+r)>>1而不是(l+r)/2.
略证:考虑奇数\(S(S>0)\),要证\((-S)>>1=\lfloor\dfrac{-S}{2}\rfloor\),只要证\(\overline{-S}-1=-S-1\),
而\(0-(\overline{-S}-1)=[2^n-(\overline{-S})]+1=S+1\),即证。
c++整数除法向0取整。
b.若\(mid\)符合条件,则区间向右缩小,如图:
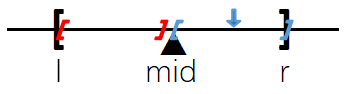
由1知,当\(mid\)符合条件时,\([l,r]\rightarrow[mid,r]\);当\(mid\)不符合条件时,\([l,r]\rightarrow[l,mid-1]\)
由2知,\(\left\{\begin{array}{ll}mid>l,\\mid-1<r\end{array}\right.\Leftrightarrow l<mid<r+1\)
易知\(x\leqslant\lceil x\rceil< x+1\),故选择\(mid=\lceil\dfrac{l+r}{2}\rceil\)时有\(\dfrac{l+r}{2}\leqslant mid<\dfrac{l+r}{2}+1\),
由1知,\(l<r\),故\(mid\geqslant\dfrac{l+r}{2}>\dfrac{l+l}{2}=l,mid<\dfrac{l+r}{2}+1<\dfrac{r+r}{2}=r+1\),
即\(l<mid<r+1\),符合条件。
实现:
细节:
1.由于上取整不易直接使用下取整来表示,我们先对可能的结果进行讨论:若\(\dfrac{x}{2}\in \mathbb{Z}\),则\(\lceil\dfrac{x}{2}\rceil=\dfrac{x}{2}\);若\(\dfrac{x}{2}\in \mathbb{Q}\),则\(\dfrac{x}{2}\)可写作\(\overline{n.5}\)的形式,\(\lceil\dfrac{x}{2}\rceil=\lfloor\dfrac{x}{2}\rfloor+1\).
不难发现,此时\(\lceil\dfrac{x}{2}\rceil=[\dfrac{x}{2}]\),对\(\dfrac{x}{2}\)进行四舍五入即可求得\(\lceil\dfrac{x}{2}\rceil\)的值。
而\([x]=\lfloor x+0.5\rfloor\)(\(\{x\}\geqslant0.5\)将进位),故\(\lceil\dfrac{l+r}{2}\rceil=[\dfrac{l+r}{2}]=\lfloor\dfrac{l+r}{2}+0.5\rfloor=\lfloor\dfrac{l+r+1}{2}\rfloor\),写作(l+r+1)>>1.
值得注意的是,我们认为答案位于\([l,r]\)中,事实上已经假设有解;若\([1,n]\)中无解,以符合便向左缩小情况为例,每一个\(mid\)都不符合条件,答案区间最终会向右缩小至n,而我们并没有判断n是否符合条件。一方面,我们可以特判n,另一方面,我们可以将求解范围扩展至\([1,n+1]\),这样,当无解时范围将会被缩小至n+1,显然超出求解范围,便能快速判断是否无解。
符合便向右缩小情况类似,扩展至\([0,n]\)即可。
总结:
| 左 | 右 | |
|---|---|---|
| mid符合 | r = mid | l = mid |
| mid不合 | l = mid+1 | r = mid-1 |
| mid取值 | \(\lfloor\dfrac{l+r}{2}\rfloor\) | \(\lceil\dfrac{l+r}{2}\rceil=[\dfrac{l+r}{2}]\) |
| 代码实现 | (l+r)>>1 | (l+r+1)>>1 |
| 无解判定 | \([1,n+1]\) | \([0,n]\) |
简记:左下右上
c++ STL中lower_bound与upper_bound函数实现了在一个序列中二分查找某个整数x的后继。
问题写法:
1.\(l=mid+1,r=mid-1\):符合便向左缩小时\(r\)缩过头导致\(mid\)丢失;符合便向右缩小时\(l\)缩过头导致\(mid\)丢失
2.\(l=mid,r=mid\):符合便向左缩小时\(l\)未缩到位导致\(mid+1\)混入;符合便向右缩小时\(r\)未缩到位导致\(mid-1\)混入
实数域上的二分¶
实现1:精度控制
while (l + eps < r) { // 1.
double mid = (l + r) / 2; // 2.
if (check(mid)) r = mid;
else l = mid;
}
细节:
1.eps为精度,即\(r-l<eps\),若保留k位小数,一般取\(eps=10^{-(k+2)}\),此时出现\(l+eps\)发生进位的概率极小,几乎能求出正确结果。
2.此处\(l,r\)为浮点数,做实数运算。
实现2:固定次数
const int K = 100;
for (int i = 0; i < K; i++) {
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
三分法求单峰函数极值¶
定义:拥有唯一极值点,且极值点两侧严格单调
思路:分类讨论
以单峰函数为例,在定义域\([l,r]\)任取两点\(lmid,rmid(lmid<rmid)\),则
当\(f(lmid)<f(rmid)\)时,如图:
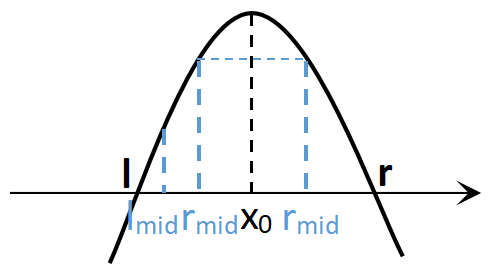
由于\(rmid\)位置不确定,而\(lmid\)一定在\(x_0\)左侧(由\(lmid<rmid\)限制),故利用\(lmid<x_0\)确定极值点比\(lmid\)大,将\(l\)缩小至\(lmid\);
当\(f(lmid)>f(rmid)\)时,如图:
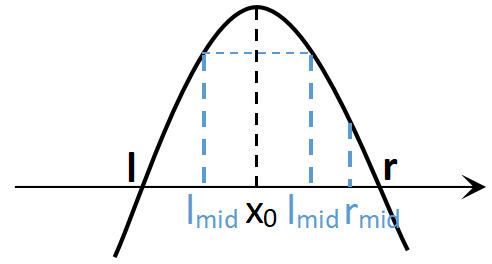
同理,利用\(rmid>x_0\)将\(r\)缩小至\(rmid\);
当\(f(lmid)=f(rmid)\)时,如图:
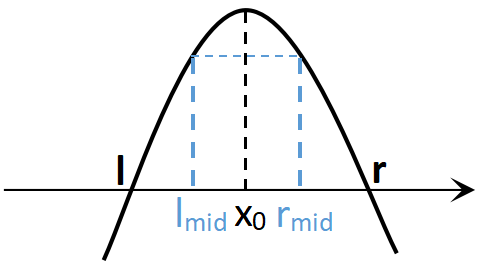
由于该函数在极值点两侧具有严格单调性,故\(lmid,rmid\)一定位于\(x_0\)两侧,可将\(l\)缩小至\(lmid\),\(r\)缩小至\(rmid\).
在此基础上,取\(lmid,rmid\)为\([l,r]\)三等分点,每次将范围缩小\(\dfrac{1}{3}\),或取\(lmid,rmid\)靠近中点,可将范围近似缩小\(\dfrac{1}{2}\),在\(O(logn)\)的时间中求得最值。
二分答案转化为判定¶
二分的本质¶
二分的本质是寻找被二分量对应的合法与不合法的边界处的合法值。
为了证明这一性质,我们先对上述表述进行简化:
1.将\([l,r]\)中每一个数以\(check(i)=0/1\)代替(未进行判定的用?代替),表示取该值时是否合法;
2.将符合便向左缩小情况记作\(+1\),将符合便向右缩小情况记作\(1+\).
对于\(+1\)型,我们先考虑一般情况,即判定过程中即有符合情况,又有不符合情况。在最后一次区间缩小前,应为\(0[1,1]\).接着计算出\(check(mid)=1\)(下取整,左侧1),缩小后得到\(0[1]1\),即求得\(0,1\)边界处对应为1的值。
再考虑特殊情况:
当判定过程仅有符合情况时,最后一次缩小前为\([?,1]\).接着将会计算并确定?的值,如果\(?=0\),缩小后得到\(0[1]\),符合;如果\(?=1\),缩小后得到\([1]1\),为最左边的符合条件的值。
当判定过程仅有不符情况时,最后一次缩小前为\(0[?,?]\).接着将会计算并确定左侧?的值,如果\(?=1\),缩小后得到\(0[1]?\),符合;如果\(?=0\),缩小后得到\(0[?]\),需进行特判,与上述无解处理一致。
对于\(1+\)型,同理,一般情况时最后一次缩小前为\([1,1]0\),缩小为\(1[1]0\),符合;
仅有符合情况时,最后一次缩小前为\([1,?]\),接着确定?的值,\(?=0\)缩小为\([1]0\),符合;\(?=1\)缩小为\(1[1]\),为最右边的符合条件的值;
仅有不符情况时,最后一次缩小前为\([?,?]0\).接着确定右侧?的值,\(?=1\)缩小为\(?[1]0\),符合;\(?=0\)缩小为\([?]0\),需进行特判,与上述无解处理一致。
这样我们就证明了二分的本质。
我们可以定义广义的二分单调性,即通过对某一点情况的考察,能判断解位于该点左侧或右侧。
在此基础上,对于一个不具有一般意义下的单调性问题,我们将1用\(↗\)代替,0用\(↘\)代替,可将其图示为(以\(+1\)型为例):

不难发现,二分法事实上求得的是极值点,且\(+1\)型求得的是极小值点,\(1+\)型求得的是极大值点。
进而推广到\(+1\)型求得的是一个形如\(0[1]\)的分界,而\(1+\)型求得的是一个形如\([1]0\)的分界;更一般的,1,0不一定为合法状态和非法状态,可以为任意的两个状态。
最优化问题¶
最优化问题中最终价值具有单调性(较小合法、过大非法或较大合法、过小非法),所以我们对最终价值进行二分,进而求得最优化的价值。
在这一过程中,我们将整个问题转化为了判定最终价值是否合法,即二分答案转化为判定。
例1 Best Cow Fences
思路:二分答案+前缀和
当最终价值(平均数)过小或过大时都非法,形成\(↗↘\)形式的单调性,故可用二分法(1+型)求最值。
判断二分形式:1.表达单调性 2.将极值点记作+,将\(↗\)记作1
对最终价值进行二分,问题转化为判定是否存在一个长度不小于F的连续子段,使得其平均数大于等于给定的二分值,即\(\dfrac{1}{n}\sum a_i\geqslant avg\)。
为了便于计算,我们将等式右边化为0,即
\(\sum a_i\geqslant n*avg\Leftrightarrow\sum(a_i-avg)\geqslant0\)
故把数列中每一个数减去二分值,并判断是否存在一个长度不小于F的连续子段,子段和非负。
部分和使用前缀和简化计算,取\(a_{j+1..i}(i\geqslant j+F)\),则
\(\max\sum\limits_{k=j+1}^i a_k=\max\limits_{F\leqslant i\leqslant n}\{S_i-\min\limits_{0\leqslant j\leqslant i-F}S_j\}\)
并且\(\min\limits_{0\leqslant j\leqslant i-F}S_j\)可随i变化动态更新。
实现:
bool check(double avg) {
double ret = -1, tmp = INT_MAX;
for (int i = 1; i <= n; i++)
cur = a[i] - avg, s[i] = cur + s[i - 1];
for (int i = f; i <= n; i++)
tmp = min(tmp, s[i - f]), ret = max(ret, s[i] - tmp);
return ret >= 0;
}
int main() {
double l = 1, r = INF, eps = 1e-5; // 保留三位小数
cin >> n >> f;
for (int i = 1; i <= n; i++)
cin >> a[i];
while (l + eps < r) {
double mid = (l + r) / 2;
if (check(mid))
l = mid;
else
r = mid;
}
cout << (int)(r * 1000) << endl;
}
例2 Innovative Business
思路:二分答案
本题即要求有向完全图(竞赛图)的Hamilton路径(不重不漏经过所有点的路径)。
先证本题有解,即任意竞赛图都存在Hamilton路径。
下对图中节点数\(n\)用数学归纳法:
当\(n=1,2\)时,显然;
当\(n\geqslant3\)时,假设\(n=k\)时结论成立,即\(k\)点的竞赛图存在Hamilton路径;
当\(n=k+1\)时,有以下三种情况:
1.第k+1点有一条指向原Hamilton路径起点的出边,如图:
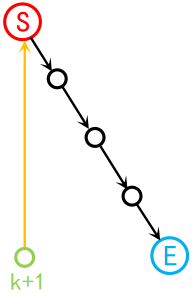
那么我们直接将它作为新Hamilton路径的起点;
2.第k+1点有一条被原Hamilton路径终点指向的入边,如图:
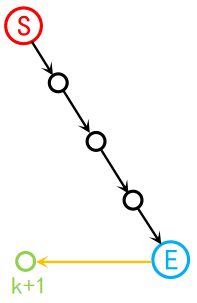
那么我们直接将它作为新Hamilton路径的终点;
3.若以上两种情况都不符合,即第k+1点被原Hamilton路径起点指向的入边,有指向原Hamilton路径终点的出边,如图:
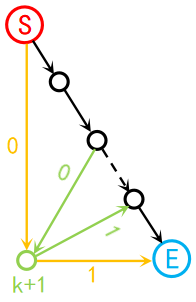
方便起见,我们将指向第k+1点的入边记作0,由第k+1点发出的出边记作1,问题转化为证明0-1串\(0…1\)中存在相邻两数为\(01\).
采用反证法,若该0-1串中任意相邻两数都相等,易知此时该串末尾的数为0,矛盾!
故存在相邻两数不等,且从左往右第一个出现的组合一定为\(01\)(两数之前都是0),即证。
那么我们只要将第k+1点连入涉及到的两点之间即可。
由归纳原理知,结论成立。
回到原题,仿照上述数归思路,我们可以逐个确定元素的位置,将第k+1个元素放入已排好序的前k个元素中去。由于放置点为出边状态和入边状态的边界,具有\(↘↗\)的局部单调性,故可用二分法(+1型)求解。
实现:
vector<int> specialSort(int N) {
vector<int> ans;
ans.push_back(1);
if (N == 1)
return ans;
if (compare(1, 2))
ans.push_back(2);
else
ans.insert(ans.begin(), 2);
if (N == 2)
return ans; // 特判n = 1, 2
for (int i = 3; i <= N; i++) {
int l = 1, r = i; // 1.
while (l < r) {
int mid = (l + r) >> 1;
if (compare(i, ans[mid - 1])) // 下标从0开始
r = mid;
else
l = mid + 1;
}
ans.insert(ans.begin() + l - 1, i); // 2.
}
return ans;
}
细节:
1.此处需对“无解”情况进行处理:本题实际上将某数插入至\(0\downarrow1\)处,仅有符合情况时,会插入至\(\downarrow1\)处,符合条件;而仅有不符情况时,会插入至\(0\downarrow0\)处(未对末位0作判定)导致结果出错,故需向右拓宽区间,使得此情况能插入至\(0\downarrow\)处。
2.向vector中插入某元素:\(v.insert(v.begin() + pos, val);\)将val插入至第pos位(下标从0开始)前(使val放置在第pos位)。