PRML读书会第五期——概率图模型(Graphical Models)

Info

本文为浙江大学人工智能协会(ZJUAI)PRML读书会系列活动会议记录。

问题的提出

概率论的基本规则

研究对象

高维随机变量：\(\vec x=(x_1,x_2,\cdots,x_p)\)，下文记作\(X\)（其中p为随机变量的维数）

基本记号

联合概率密度：\(p(x_1,x_2,\cdots,x_p)\)（下文简称联合概率）

边缘概率：\(p(x_i)\)

条件概率：\(p(x_j|x_i)\)

基本规则

• Sum Rule：\(p(x_1)=\int p(x_1,x_2)dx_2\)

对于离散变量，只需用求和替代积分即可；下文默认采用积分符号

• Product Rule：\(p(x_1,x_2)=p(x_1)p(x_2|x_1)=p(x_2)p(x_1|x_2)\)
• Chain Rule：\(p(x_1,x_2,\cdots,x_p)=\prod\limits_{i=1}^pp(x_i|x_1,\cdots,x_{i-1})\)
• Bayesian Rule：\(p(x_2|x_1)=\dfrac{p(x_1,x_2)}{p(x_1)}=\dfrac{p(x_2)p(x_1|x_2)}{\int p(x_1,x_2)dx_2}=\dfrac{p(x_2)p(x_1|x_2)}{\int p(x_2)p(x_1|x_2)dx_2}\)

注：

1. 四条法则内在的逻辑关系：加法法则与乘法法则为基本法则，链式法则为乘法法则高维形式的推广，贝叶斯法则为反复利用加法法则与乘法法则求后验概率

2. 链式法则的推导：

法一：从后向前

记\(x_1,x_2,\cdots,x_{p-1}\)为\(X\setminus x_p\)，将\(X\setminus x_p\)看作\(x_1\)，\(x_p\)看作\(x_2\)，利用乘法法则得： $$ p(X\setminus x_p,x_p)=p(X\setminus x_p)p(x_p|X\setminus x_p)=p(x_1,x_2,\dots,x_{p-1})p(x_p|x_1,x_2,\dots,x_{p-1}) $$ 对于联合概率\(p(x_1,x_2,\cdots,x_{p-1})\)，重复上述操作，向前递推即可。

*本文所有形如\(X\setminus x_p\)的记号含义与\(X\setminus \{x_p\}\)一致

法二：从前向后

从条件概率的本质出发：在已有变量的条件下的概率。

这样，我们先考虑\(x_1\)，概率为\(p(x_1)\)；在此基础上，我们再考虑\(x_2\)，由于此时处于已有\(x_1\)的条件下，故概率为\(p(x_2|x_1)\)；利用乘法法则将两步操作连接起来，即有\(p(x_1,x_2)=p(x_1)p(x_2|x_1)\).按同样的方式依次考察剩余的变量，即得：

$$ p(x_1,x_2,\dots,x_p)=p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)\dots p(x_p|x_1,x_2,\dots,x_{p-1})=\prod\limits_{i=1}^pp(x_i|x_1,\dots,x_{i-1}) $$

特别的，当\(i=1\)时，\(p(x_1|\phi)\triangleq p(x_1)\)

困境与模型简化

以计算联合概率为例，我们会发现这样一个问题：当随机变量维度过高时，计算将变得非常复杂，\(p(x_1,x_2,\cdots,x_p)\)计算量太大。

计算复杂的根本原因是变量间的依赖关系过于复杂。针对这一问题，我们可以提出以下假设：

• 相互独立

我们认为所有变量之间相互独立，意味着\(\forall x_i\in X,X_s\subset X\setminus x_i,p(x_i|X_s)=p(x_i)\)，即对于任何一个变量，其它变量的存在并不会影响到它的边缘概率。那么联合概率的计算可以简化为： $$ p(x_1,x_2,\dots,x_p)=\prod\limits_{i=1}^pp(x_i) $$ 典型的应用有朴素贝叶斯算法(Naive Bayes)，其核心假设为\(p(x|y)=\prod\limits_{i=1}^pp(x_i|y)\).

可是这种假设太强，我们需要适当的引入变量之间的依赖关系来增强模型的表达能力。

• （齐次）马尔可夫假设

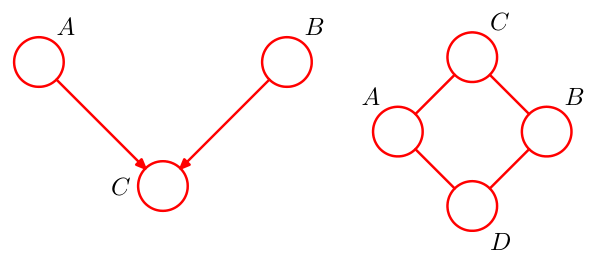
如图，我们向相互独立的模型中引入这样的依赖关系：所有的变量都唯一地依赖于前一个变量，再往前的变量都与之无关，例如\(p(x_3|x_1,x_2)=p(x_3|x_2)\)，当\(x_2\)被观测后，\(x_1\)对\(x_3\)不造成影响，换句话说在确定（观测）\(x_2\)的条件下，\(x_1\)与\(x_3\)独立，记作\(x_1\perp \!\!\! \perp x_3|x_2\).(其中\(\perp \!\!\! \perp\)为条件独立符号)

注：齐次马尔可夫假设的原始表述为：t+1时刻的状态只依赖于t时刻的状态，与观测状态无关

更一般的，我们可以将该假设中的条件独立性记为：

\[x_j\perp\!\!\!\perp x_{i+1}|x_i,i<j\]

当\(x_i\)被观测后，下一个状态\(x_{i+1}\)将与\(x_i\)之前的状态都独立，即\(x_{i+1}\)只与\(x_i\)有关，而与\(x_1,x_2,\cdots,x_{i-1}\)无关。

该假设中的条件独立性被称为马尔可夫性(Markov Property).典型的应用有隐马尔可夫模型(HMM)，其核心假设即为齐次马尔可夫假设。

可是这种假设依赖关系较单调，表达能力仍有提升空间。

条件独立性

进一步讨论马尔可夫假设。我们可以对上述齐次马尔可夫假设进行泛化处理，将条件独立性作用在变量集合上：

\[X_A\perp\!\!\!\perp X_B|X_C\]

其中\(X_A,X_B,X_C\)为变量集合，且互不相交。式子的含义简单明了：在观测到变量集合\(X_C\)中的全部变量的条件下，变量集合\(X_A\)与\(X_B\)中的变量将变得相互独立。

事实上，概率图模型正是将图作为可视化的工具，将抽象的条件独立性以图的形式形象地表达出来。

概率图模型的基本概念

概率图，顾名思义，我们需要研究其中概率的成分与图的成分。上文中，我们已经充分讨论了有关概率的部分。再进一步探讨图的成分前，先建立对概率图模型研究的基本思路。

在概率图模型中，我们主要研究以下三个问题：概率图模型的表示、推断与学习，如图所示：

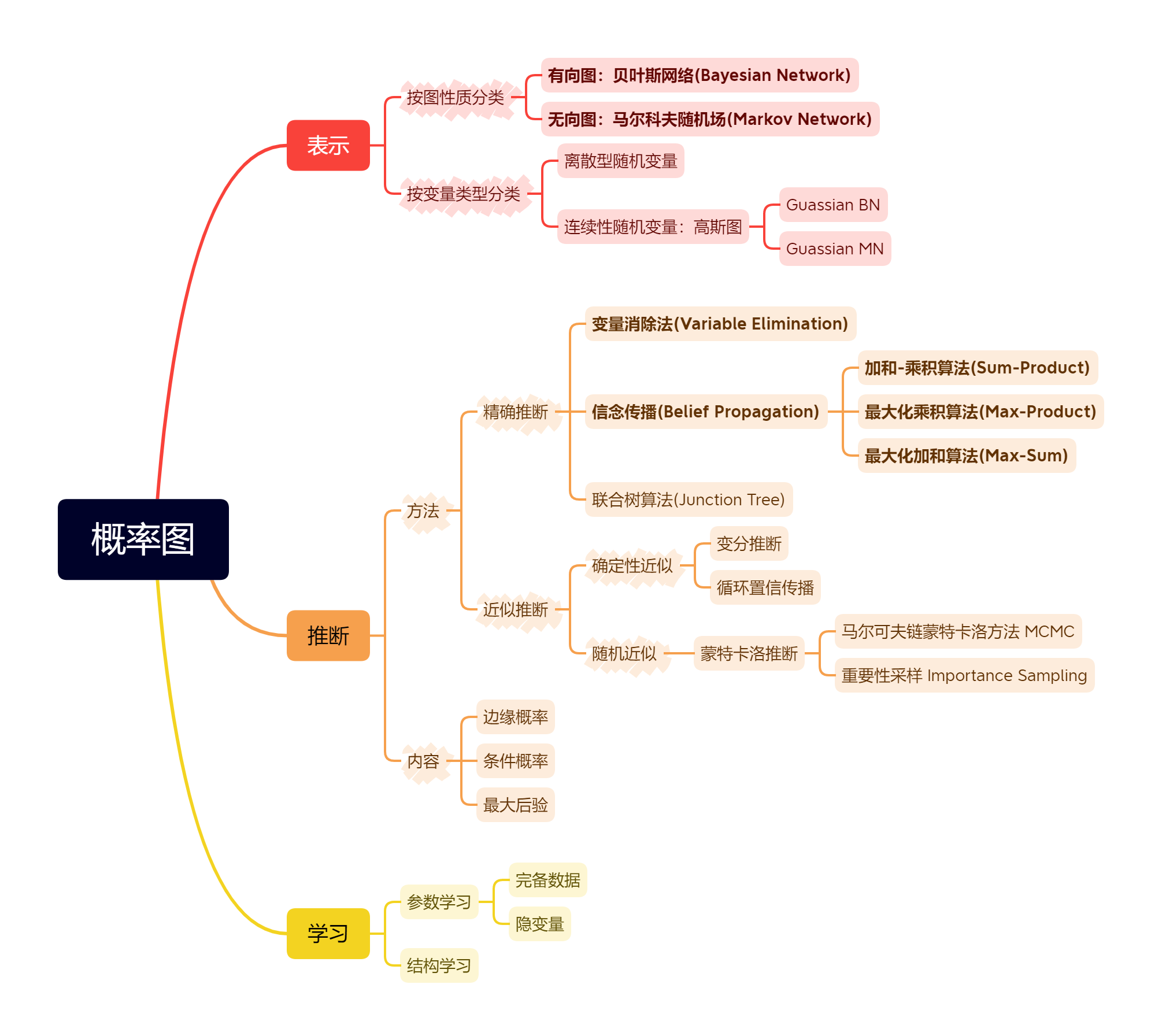
本章中，我们将重点讨论加粗部分的内容。接下来，我们先讨论概率图的表示。

贝叶斯网络(Bayesian Network)

基本概念

贝叶斯网络即用有向图表示变量的联合概率，其中有向图的节点代表随机变量，而箭头的方向是对条件概率进行描述。

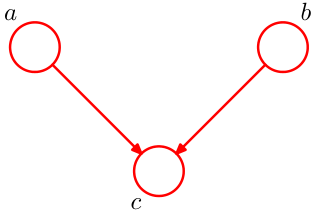
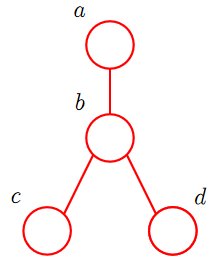
由于贝叶斯网络是对变量的联合概率进行描述，我们先从变量的联合概率入手。假设我们有三个变量\(a,b,c\)，利用链式法则，我们可以写出它们的联合概率： $$ p(a,b,c)=p(a)p(b|a)p(c|a,b) $$

注：在涉及概率图模型的探讨中，不在记号上对变量\(x_a\)与节点\(a\)做区分，二者含义一致

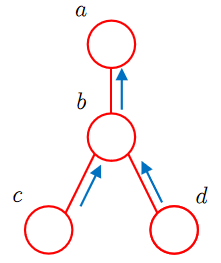
观察联合概率的表达式，我们发现，计算b的概率时“依赖”于a，计算c的概率时“依赖”于a,b。我们可以作出它对应的贝叶斯网络：

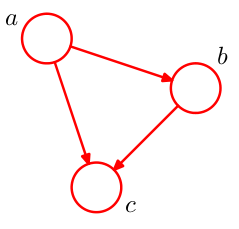
如图，节点a为节点b的父节点，当且仅当变量b“依赖”于变量a.为了清晰的描述所谓的“依赖”关系，我们将联合概率写作如下形式： $$ p(x_1,x_2\dots,x_p)=\prod\limits_{i=1}^pp(x_i|pa_i) $$

链式法则：\(p(x_1,x_2,\cdots,x_p)=\prod\limits_{i=1}^pp(x_i|x_1,\cdots,x_{i-1})\)

并称之为因子分解。因子分解形式中，\(x_i\)“依赖”于它的因子中以条件形式出现的所有变量。对应的，这些被“依赖”的变量就会成为\(x_i\)的父节点，\(pa_i\)即为\(x_i\)的父节点集合。

为了从联合概率的因子分解形式得到对应的贝叶斯网络，我们首先要明确“依赖”关系，确定谁是谁的父节点。在此基础上，我们对这些节点进行拓扑排序，即可做出对应的贝叶斯网络。

反过来，利用因子分解，我们也可以轻易地得到这些变量对应的联合概率。

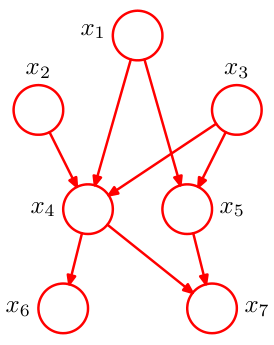
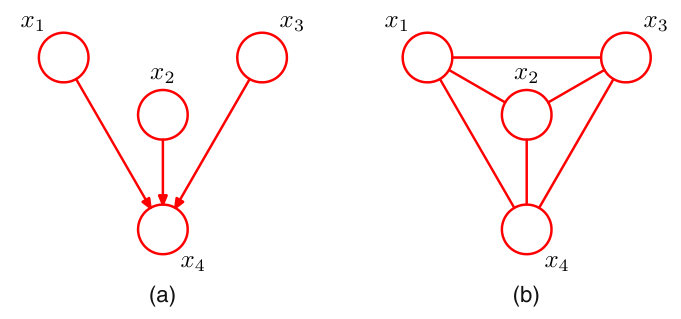
例如上图，我们可以直观的看到\(x_4\)的父节点是\(x_1,x_2,x_3\),\(x_5\)的父节点是\(x_1,x_3\)，以此类推，按照因子分解的形式，我们可以写出它的联合概率： $$ p(x_1,x_2,\dots,x_7)=p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3)p(x_5|x_1,x_3)p(x_6|x_4)p(x_7|x_4,x_5) $$

注：当存在相同形式的依赖关系（如多个变量都唯一的依赖于同一个变量）时，我们可以引入板的记号来进一步简化表达：

如图，左图表示的关系与右图一致。

基本结构

为了高效的分析更加复杂的贝叶斯网络，我们需要对构成贝叶斯网络的基本结构进行研究。

为了明确的称呼这些基本结构，我们做如下规定：

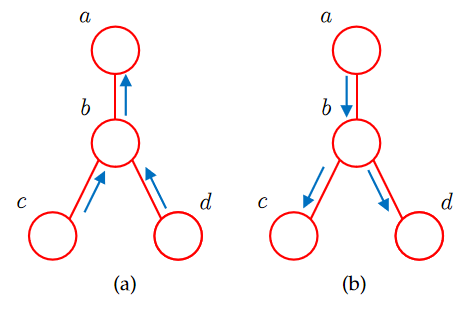
如图，我们将有向边即箭头的箭镞称为head,将箭头的箭杆成为tail。

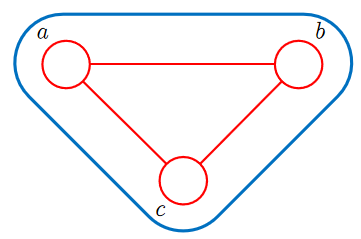
tail-to-tail

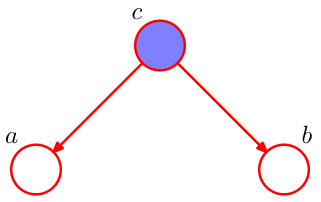
如图，节点c与两边的tail相连。写出它的因子分解，可以得到： $$ p(a,b,c)=p(a|c)p(b|c)p( c) $$ 我们有两种方法可以得出背后蕴含的条件独立性。

法一：考虑链式法则给出的联合概率\(p(a,b,c)=p( c)p(b|c)p(a|b,c)\)，注意，此处的联合概率并未考虑任何的条件独立性。

两式联立，得： $$ p( c)p(b|c)p(a|b,c)=p(a|c)p(b|c)p( c) $$ 两边同除\(p( c)p(b|c)\)，即得\(p(a|b,c)=p(a|c)\).这意味着在给定c的条件下，b对a并未产生任何影响，即

\[a\perp\!\!\!\perp b|c\]

法二：倘若没有任何一个变量被观测，利用加法法则，我们可以求出边缘概率\(p(a,b)=\int p(a|c)p(b|c)p( c)dc\)，而等式右边往往难以被分解为\(p(a)p(b)\)，因此，\(a\not\!\perp\!\!\!\perp b|\phi\).

在给定c的条件下，利用贝叶斯法则，我们可以得到后验概率\(p(a,b|c)\)： $$ p(a,b|c)=\dfrac{p(a,b,c)}{p( c)}=p(a|c)p(b|c) $$ 很显然，我们有

\[a\perp\!\!\!\perp b|c\]

为了记住最终结论，我们可以认为，对c的观测，阻断了无向路径\(a-b-c\).

head-to-tail

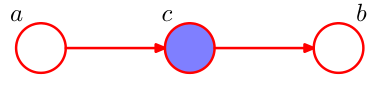
如图，节点c与a的head相连，与b的tail相连。写出它的因子分解，可以得到： $$ p(a,b,c)=p(a)p(b|c)p(c|a) $$ 仿照head-to-head中的讨论，我们同样可以采用这两种做法来寻找背后的条件独立性：

法一：

\[\begin{array}{l}p(a,b,c)=p(a)p(c|a)p(b|a,c)=p(a)p(b|c)p(c|a)\\\Rightarrow p(b|a,c)=p(b|c)\Rightarrow a\perp\!\!\!\perp b|c\end{array}\]

法二：

\[\begin{array}{l}p(a,b)=\int p(a)p(b|c)p(c|a)dc=p(a)\int p(b|c)p(c|a)dc\not=p(a)p(b)\Rightarrow a\not\!\perp\!\!\!\perp b|\phi\\p(a,b|c)=\dfrac{p(a,b,c)}{p( c)}=\dfrac{p(a)p(c|a)}{p( c)}p(b|c)=\dfrac{p(a,c)}{p( c)}p(b|c)=p(a|c)p(b|c)\Rightarrow a\perp\!\!\!\perp b|c\end{array}\]

类似的，对c的观测，阻断了无向路径\(a-c-b\).

head-to-head

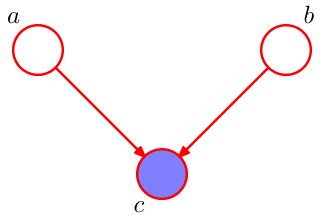
如图，节点c与两边的head相连。写出它的因子分解，可以得到： $$ p(a,b,c)=p(a)p(b)p(c|a,b) $$ 同样的，我们有两种做法：

法一：

\[\begin{array}{l}p(a,b,c)=p(a)p(b|a)p(c|a,b)=p(a)p(b)p(c|a,b)\\\Rightarrow p(b|a)=p(b)\Rightarrow a\perp\!\!\!\perp b|\phi\end{array}\]

法二：

\[\begin{array}{l}p(a,b)=\int p(a,b,c)dc=\int p(a)p(b)p(c|a,b)dc=p(a)p(b)\int p(c|a,b)dc=p(a)p(b)\Rightarrow a\perp\!\!\!\perp b|\phi\\ p(a,b|c)=\dfrac{p(a,b,c)}{p( c)}=p(a)p(b)\dfrac{p(c|a,b)}{p( c)}\not=p(a)p(b)\Rightarrow a\not\!\perp\!\!\!\perp b|c\end{array}\]

这里我们得出了非常不同的结论，默认情况下a,b独立，但在对c进行观测后，a,b反而不一定独立，变得有关了。这是贝叶斯网络的独特之处。

当我们利用法一来寻找背后的条件独立性时，我们并不能从正面严谨地得到\(a\not\!\perp\!\!\!\perp b|c\)的结论。我们可以采取举反例的方式来说明这一点。事实上，从法二中我们可以看到，造成条件独立性被破坏的根本原因在于\(p(c|a,b)\not=p( c)\)，由于c会受到a,b的影响，当我们观测c时，得到的观测值的分布并不一定与让\(a,b\)“自由”地影响c时具有的概率分布一致。

众多反例表明，\(p(a|c)>p(a|c,b)\)，在此意义上同样能够说明a,b的独立性被破坏。

作为该结论的一个推广，当c的任何子孙节点被观测到时（c可以不被观测），a,b之间的独立性同样会消失。

注：主讲人提到的“不太恰当”的例子为将其理解为亲人关系。特别的，上述head-to-head结构中，将a理解为父亲，将b理解为母亲，而c为二者的孩子，并将观测过程直观的理解为确定孩子的存在。在孩子尚未出生时，男女双方并无亲人关系，而孩子的降临将男女双方以亲人的身份联系在一起。

猜测主讲人认为该比喻不恰当的地方如下：该比喻中，是孩子的出现影响了父母的关系，而法二中指出是节点a,b对c的影响造成了独立性的消失。我认为换一种理解方式可以使该例变得恰当：正是父母想要一个孩子的行为决定了孩子的出现。在此意义上，是a,b对c造成了影响。事实上，这两种理解是相通的。

这是一个十分形象的例子，在不考虑普世道德限制的前提上，该比喻亦能很好的解释该结论的推广形式。

条件独立性

D-划分(D-separation)

回到最初的目的上，我们向一般的联合概率中引入图，是为了形象的表示这些变量之间的条件独立性。具体的来说，是为了确定变量集合\(X_A,X_B,X_C\)，使得

\[X_A\perp\!\!\!\perp X_B|X_C\]

我们有两个探讨的角度：在整体层面确定\(X_A,X_B,X_C\)（全局马尔可夫性）；在个体层面判断具体的a,b在给定观测下是否独立（局部马尔可夫性）。

先从个体层面进行讨论。对于给定节点a,b之间的任意联通路径\(P\)（\(P\)为路径上节点的集合），若\(\exists c\in P\)满足以下两个规则之一

1. \(c\in\{tail-to-tail,head-to-tail\}\)且\(c\)被观测
2. \(c\in\{head-to-head\}\)且\(\forall d\)为\(c\)及其子孙，\(d\)未被观测

则\(a\perp\!\!\!\perp b\).

再从整体层面进行讨论。对于给定的变量集合\(X_A,X_B\)，\(\forall a\in X_a,b\in X_b,\forall P\ s.t.a-P-b\)，按如下规则对\(\forall c\in P\)进行划分

1. \(c\in\{tail-to-tail,head-to-tail\}\)，则\(c\in X_c\)
2. \(c\in\{head-to-head\}\)，则\(\forall d\)为\(c\)及其子孙，\(d\notin X_c\)

换言之，所有能够通过观测以阻断a,b间联系，使得a,b独立的点c都在\(X_C\)中，如图所示：

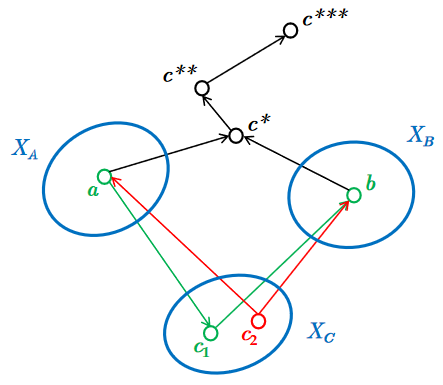
下面给出D划分的具体示例。如图，标出的为观测节点，判断a,b在观测节点的条件下是否具有独立性。

图中a,b之间具有唯一的路径\(P=\{e,f\}\).

如左图，e作为head-to-head型节点，其子孙c被观测，故不具有阻碍作用；而具备阻碍能力的tail-to-tail型节点f并未被观测，故并不具有阻碍作用，因此a,b并不独立，即\(a\not\!\perp\!\!\!\perp b|c\)；如右图，情况刚好完全相反，e,f均起到阻碍作用，故a,b独立，即\(a\perp\!\!\!\perp b|f\).

马尔可夫毯(Markov blanket)

进一步探讨变量之间的条件独立性。在相互独立的简化模型中，我们假设\(p(x_i|X\setminus x_i)=p(x_i)\).既然现在我们引入了贝叶斯网络，在此基础上再考虑条件概率\(p(x_i|X\setminus x_i)\)，利用贝叶斯法则与贝叶斯网络的因子分解可以写作 $$ p(x_i|X\setminus x_i)=\dfrac{p(x_1,\dots,x_p)}{\int p(x_1,\dots,x_p)dx_i}=\dfrac{\prod\limits_{i=1}^pp(x_i|pa_i)}{\int \prod\limits_{i=1}^pp(x_i|pa_i)dx_i} $$ 记\(\prod\limits_{i=1}^pp(x_i|pa_i)=\Delta\bar\Delta\)，其中\(\Delta\)为与\(x_i\)有关的因子之积，而\(\bar\Delta\)为与\(x_i\)无关的因子之积，则上式可进一步化简为 $$ \dfrac{\Delta\bar\Delta}{\int \Delta\bar\Delta dxi}=\dfrac{\Delta\bar\Delta}{\bar\Delta\int \Delta dxi}=\dfrac{\Delta}{\int \Delta dxi}\triangleq f(\Delta) $$ 即\(p(x_i|X\setminus x_i)\)仅与与\(x_i\)相关的条件概率有关。

从因子分解中，我们很容易找到与\(x_i\)有关的因子：\(x_i\)作为儿子的\(p(x_i|pa_i)\)与\(x_i\)作为父亲的\(p(ch_i|x_i,pa_{ch_i})\)，其中\(ch_i\)为\(x_i\)的子节点，除\(x_i\)以外的\(pa_{ch_i}\)称为\(x_i\)的同父节点。因此，与\(x_i\)有关的节点仅为其父节点、子节点与同父节点，构成下图所示的马尔可夫毯：

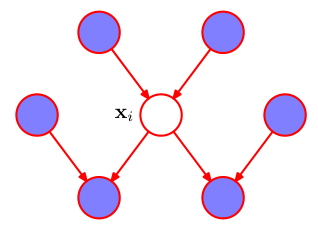
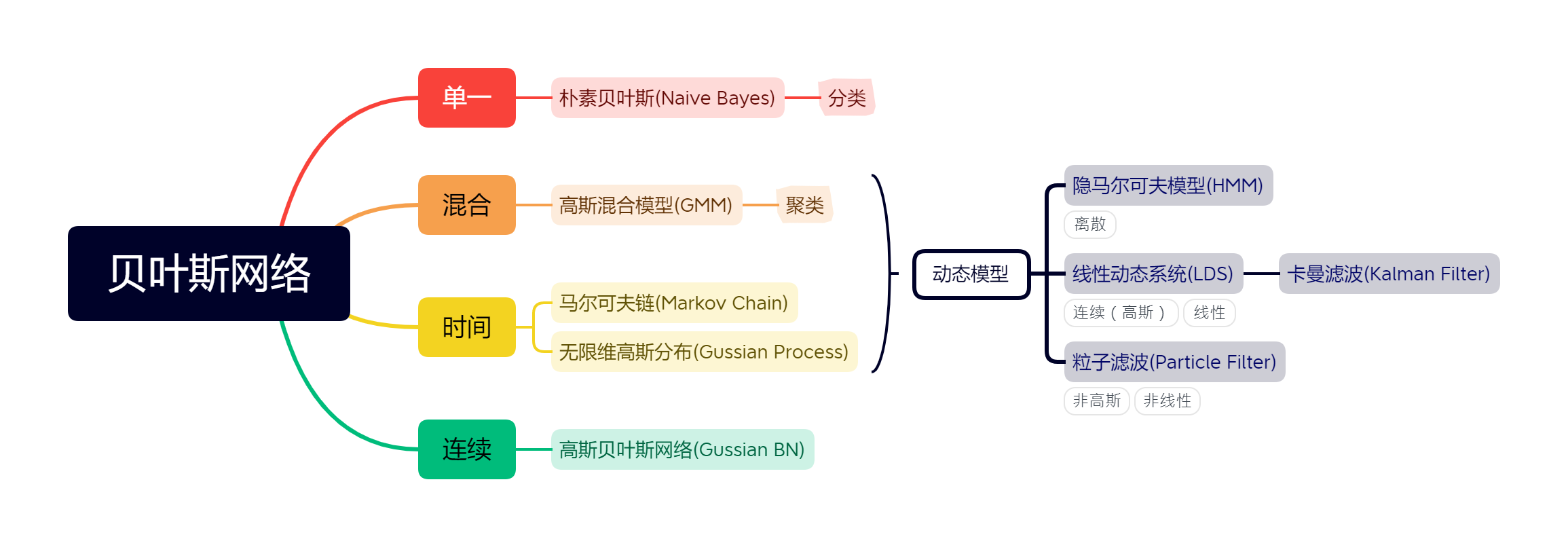
贝叶斯网络的分类及其具体模型

可以按照从单一模型到混合模型，从有限时空（离散）到无限时空（连续）将贝叶斯网络分成如下几类：

马尔可夫随机场(Markov Random Fields)

通过上述讨论，我们发现，在使用有向图表示变量的联合概率时，会出现head-to-head型较为反常的结构；而当我们利用无向图表示变量的联合概率时，由于无向边不再具有head与tail的区分，故这样的问题能很好的得到解决。

基本概念

马尔可夫随机场（又称马尔可夫网络）即是用无向图来表达变量的联合概率。在马尔可夫随机场中，无向边表示了变量之间的软约束。

与贝叶斯网络相反，讨论马尔可夫随机场的条件独立性是较为容易的。

条件独立性

马尔可夫随机场的条件独立性体现在三个方面上：全局马尔可夫性、局部马尔可夫性和成对马尔可夫性，且三者等价。

全局马尔可夫性

实际上，D-划分中的D是directing的缩写，特指的是有向图中判断条件独立性的划分方法。借助D-划分的思想，我们一样可以确定无向图中的马尔可夫性。

由于不存在head与tail之分，自然就不会出现head-to-head的情形，而tail-to-tail与head-to-tail都可以看作观测中间节点使得两端的节点被阻断，从而独立。

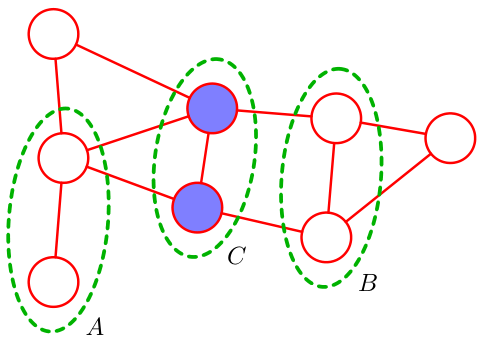
按照这样的思路，我们很容易得到无向图全局马尔可夫性。对于给定的变量集合\(X_A,X_B,X_C,\forall a\in X_A,\forall b\in X_B,\forall P\ s.t.a-P-b,\)若\(\exists c\in P\ s.t.c\in X_C\)，那么\(X_A\perp\!\!\!\perp X_B|X_C\).

如图，从A到B的所有路径都被C所阻断，即可得到\(X_A\perp\!\!\!\perp X_B|X_C\).

局部马尔可夫性

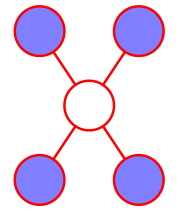
利用马尔可夫毯，我们容易发现一旦i的邻居节点（记作\(ne_i\)）被观测，那么i与除邻居节点及i以外的节点将变得条件独立，即

\[x_i\perp\!\!\!\perp X\setminus (x_i\cup ne_i)|ne_i\]

成对马尔可夫性

考虑马尔可夫网络上的任意两个没有边直接相连的节点i,j，若除i,j外所有的节点都被观测，那么由于i,j没有直接相连的边，它们之间的连接将被阻断，即

\[x_i\perp\!\!\!\perp x_j|X\setminus\{x_i,x_j\}\]

因子分解

因子分解的目的是为了体现条件独立性，以成对马尔可夫性为例，如果\(x_i\perp\!\!\!\perp x_j|X\setminus\{x_i,x_j\}\)，那么\(x_i,x_j\)应该位于不同的因子中，这样\(p(x_i,x_j|X\setminus\{x_i,x_j\})\)才有可能写成\(p(x_i|X\setminus\{x_i,x_j\})p(x_j|X\setminus\{x_i,x_j\})\)的形式。

为了实现这一目的，我们引入团(clique)的概念：团是完全子图。换句话说，团是原图上的某些节点构成的集合，并且这些节点两两相连。在此基础上我们还可以将具有如下性质的团定义最大团：不可能将图中的任何⼀个其他的节点包含到这个团中而不破坏团的性质（所含节点两两相连）。

我们将最大团记作\(C\)，最大团中变量构成的集合记作\(X_C\)，并在最大团上定义势函数\(\psi_C(X_C)\)，那么联合概率的因子分解可以写为： $$ p(X)=\dfrac{1}{Z}\prod\limits_C \psi_C(X_C) $$ 其中\(Z\)为归一化因子，为了保证\(\sum\limits_Xp(X)=1\)，有 $$ Z=\sum\limits_X\prod\limits_C\psi_C(X_C) $$

注：

1. 势函数\(\psi_C(X_C)>0\)，否则概率无法被正确的归一化
2. 对\(\prod\limits_C\)的理解：即对所有的最大团求积；\(\psi_C\)可以理解为对于不同的最大团，\(\psi_C\)的具体表达可能有不同
3. 对\(\sum\limits_X\)的理解：这里是对\(X=\{x_1,x_2,\cdots,x_p\}\)全体的求和，可以一步一步来，写作\(\sum\limits_{x_1}\sum\limits_{x_2}\cdots\sum\limits_{x_p}\)
4. 事实上，从后文的讨论中我们会发现，并不一定需要将因子分解定义在最大团上，只需保证\(C\)是团即可。但例如对于a,b,c构成的团，若写作\(\psi_a(a)\psi_b(b)\psi_c( c)\)，我们可以令\(\Psi_{a,b,c}(a,b,c)=\psi_a(a)\psi_b(b)\psi_c( c)\)，将三个因子整合在一起，又因为a,b,c构成了团，所以\(\Psi_{a,b,c}\)的表达合法，我们可以只考虑最大团，既保证了正确性，又减少了因子的数量，让式子变得更加简洁

你可能会对“势函数”这一名称感到困惑。事实上，这里是借鉴了热力学统计物理的吉布斯分布（Gibbs，又称玻尔兹曼分布）。在热力学中，我们定义\(\psi(X_C)\triangleq exp\{-E(X_c)\}\)，其中\(E(X_C)\)为能量函数，代入因子分解中，我们可以得到 $$ p(X)=\dfrac{1}{Z}\prod\limits_Cexp{-E(X_c)}=\dfrac{1}{Z}exp{-\sum\limits_CE(X_C)} $$ 进一步地，我们可以将它化作指数族分布： $$ p(X)=h(X)exp{\eta^T\phi(X)-A(\eta)}=\dfrac{1}{Z(\eta)}h(X)exp{\eta^T\phi(X)} $$ 类似的，在热力学中，我们利用最大熵原理，同样可以得到指数族分布的最终结果。

事实上，利用Hammesley-Clifford定理可以证明吉布斯分布与马尔可夫随机场的等价性，由于定理的证明较为繁琐，我将其放在附录中，有兴趣的读者可以自行查阅。

无向图与有向图的关系

通过上述讨论，我们发现马尔可夫随机场相较于贝叶斯网络，由于没有head-to-head的异常结构，条件独立性的表达将变得非常直观。有没有一种方法能够让我们将有向图转化为无向图呢？

道德图(Moral Graph)

答案是肯定的。概率图模型的设计初衷是将抽象的条件独立性通过图的结构具象的表达出来，而联合概率的因子分解形式是条件独立性的数学表达，所以我们只需要考察转化前后的因子分解即可。

按照上文讨论有向图D-划分时的思路，我们依次考察三种基本结构。

对于tail-to-tail结构，如图：

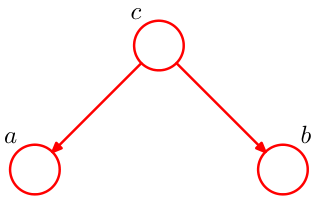
写出它的因子分解： $$ p(a,b,c)=p(a|c)p(b|c)p( c) $$ 调整一下顺序，我们有

\[ p(a,b,c)=\underbrace{p(a|c)p( c)}_{\psi_{a,c}}\underbrace{p(b|c)}_{\psi_{b,c}} \]

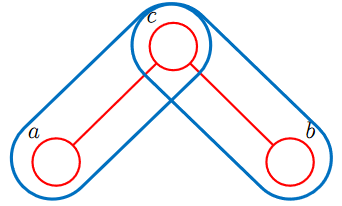
正好对应无向图的因子分解（其中最大团为\(\{a,c\},\{b,c\}\)）：

\[ p(a,b,c)=\dfrac{1}{Z}\psi_{a,c}(a,c)\psi_{b,c}(b,c) \]

故tail-to-tail结构的道德图直接将有向边改为无向边即可。

对于head-to-tail结构，如图：

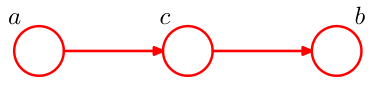
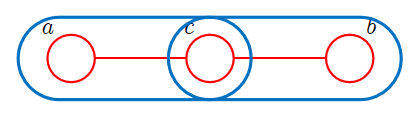
类似的，我们有

\[ p(a,b,c)=p(a)p(b|c)p(c|a)=\underbrace{p(a)p(c|a)}_{\psi_{a,c}}\underbrace{p(b|c)}_{\psi_{b,c}}=\dfrac{1}{Z}\psi_{a,c}(a,c)\psi_{b,c}(b,c) \]

故对应的道德图为

对于head-to-head结构，如图：

类似的，我们有

\[ p(a,b,c)=p(a)p(b)p(c|a,b)=\underbrace{p(a)p(b)p(c|a,b)}_{\psi_{a,b,c}}=\dfrac{1}{Z}\psi_{a,b,c}(a,b,c) \]

故对应的道德图为

与前两种基本结构不同的地方在于，由于项\(p(c|a,b)\)的存在，它只能被归入\(\psi_{a,b,c}\)中，故最终得到的道德图中\(a,b,c\)整体以最大团的形式出现，换言之，\(a,b\)之间产生了连边。

事实上，这是道德图命名的由来之处，\(a,b\)产生连接的过程被称为“伦理”(moralization)，伦理过程后的图被称作道德图。

注：中文版给出的翻译为“伦理”，可能参考了将图理解为亲人关系的比喻；原文的确切翻译为“道德教化”，较为抽象

综上，我们将有向图转换为对应的道德图有赖于一下两条规则：

1. 对于图中任何节点i，将\(pa_i\)中的节点两两相连
2. 将图中的所有有向边替换为无向边

例如下面的有向图(a)，按照上述规则我们很容易得到它对应的道德图(b)：

图的表达能力

通过对道德图的讨论，我们可以对有向图与无向图在表达条件独立性这一具体任务下的表达能力做一个总结。

直观的来说，二者的关系可以表为如下的韦恩图：

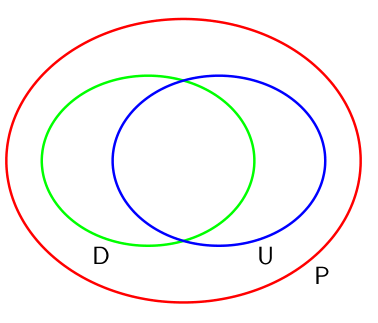
其中\(P\)为所有概率分布组成的全集，而\(D,U\)分别为有向图和无向图能完美表达的概率分布的部分。

至于何为完美，原书中引入如下两个概念：

• 依赖图(Dependency map,D图)：如果⼀个概率分布中的所有条件独立性质都通过⼀个图反映出来，那么这个图被称为这个概率分布的D图，比如完全非连接的散点图（分布的独立性\(\subset\)图的独立性）

• 独立图(Independence map,I图)：如果⼀个图的每个条件独立性质都可以由⼀个具体的概率分布满足，那么这个图被称为这个概率分布的I图，比如完全连接的完全图（图的独立性\(\subset\)分布的独立性）

既是依赖图又是独立图的图被称作完美图。

其中\(D\)与\(U\)的交集即为刚才讨论的一部分道德图，而有部分的图位于\(D\setminus U\)与\(U\setminus D\)的部分，如下：

左图原先表达的\(A\perp\!\!\!\perp B|\phi,A\not\!\perp\!\!\!\perp B|C\)，无法同时在一张具有三个点的无向图中表出；同样，右图原先表达的\(A\not\!\perp\!\!\!\perp B|\phi,A\perp\!\!\!\perp B|C\cup D,C\perp\!\!\!\perp D|A\cup B\)也无法同时在一张具有四个点的有向图中表出。

推断概述

利用概率图模型，我们可以解决以下几类推断任务：

• 边缘概率\(p(x_i)\)：利用加法法则，\(p(x_i)=\sum\limits_{x_1}\sum\limits_{x_2}\cdots\sum\limits_{x_{i-1}}\sum\limits_{x_{i+1}}\cdots\sum\limits_{x_p}p(X)=\sum\limits_{X\setminus x_i}p(X)\)
• 条件概率\(p(X_A|X_B)\)：利用贝叶斯法则
• 最大后验\(X^{max}=\mathop{\arg\max}\limits_X\ p(X)\)

注：从推断部分起，我们默认所有随机变量变量都是离散的；对于连续型随机变量，只需将求和改为积分即可

下文我们主要讨论精确推断，精确推断有如下几种方法：

• 变量消除法(Variable Elimination)

回到我们的具体任务上来。当我们利用加法法则进行推断时，我们的核心做法是对联合概率进行求和。稍后我们会看到，直接利用变量消除法暴力的计算边缘概率会造成计算复杂度极高的问题。但从上述对因子分解的讨论中我们不难看出，联合概率中的部分因子与某些变量并无直接关联。这样，我们就可以利用乘法对加法的分配率，将部分无关因子从求和式中提出，进而简化我们的运算。由于将某因子提出后，剩余的和式中的总变量得以减少，故名之曰变量消除。

• 信念传播(Belief Propagation)

利用变量消除法，在同一个概率图上求解不同随机变量的边缘概率时，会出现重复计算的问题。而信念传播的本质是为了减少重复的计算，将计算结构存储下来，空间换时间，进一步优化算法效率。

信念传播算法提出“信息”(message)的概念，将这些在不同计算中出现重叠的部分以“信息”的形式进行传递。这些重叠部分互相引用的特点构成了传递的基础，如同不断传播的信念，正是算法名称的由来之处。

纯粹的变量消除法还会带来这样一个问题：我们难以确定变量的最优消除次序（属于NP-Hard问题），从图结构出发来安排变量的消除次序是信念传播的另一大优势所在。

结合上述的乘法对加法的分配律，利用信念传播的思想，就有了著名的Sum-Product算法（加和-乘积算法）。加和-乘积算法在不同的图结构上有不同的作用范围，下文我们主要在引入因子节点的因子图的基础上讲解Sum-Product算法，事实上我们也可以完全脱离因子的概念得到该算法的另一种版本，我将在附录中进行讲解，供兴趣的读者参考。形式不同，思想相同，作用范围略有不同：前者因因子图的特性，能处理在有向图转化为对应道德图时产生的环结构，而后者仅能处理树结构。

事实上，这样的算法步骤亦可用于最大后验的求解，由于乘法对max函数同样具有分配律，我们只需对Sum-Product算法稍加修改就可以得到Max-Product算法（最大化乘积算法）。由于Max-Product中涉及连续的乘法操作，对于概率这种小数据来说，精度的保持较为困难，我们可以简单的给两边取一个对数，这样乘法就化为了加法，简单优化后的Max-Sum算法（最大化加和算法）能很好的解决精度问题。

• 联合树算法(Junction Tree)

上文中提到的Sum-Product算法（及其衍生算法）都难以直接运用到一般的图结构中。从图本身的性质出发，我们可以对图进行一些变换，使得这些算法能被很好的运用到一般的无环图中，而算法的基本思想并没有改变。

对于有环图，由于环的存在，我们难以对其进行精确推断，在这种图结构中我们只能采取近似推断的方法。循环置信传播是一种在某些情况下能发挥巨大作用的确定性近似方法。

上述的联合树算法与近似推断方法，并不在我们的讨论范围内。有兴趣的读者请自行查阅相关资料。

Sum-Product算法

预备

在继续下文的讨论之前，为了更好的利用乘法分配率，将我先加深一下对\(\sum\)符号的理解。

• 对多个变量求和：\(\sum\limits_a\sum\limits_b\)可以简写为\(\sum\limits_{a,b}\)；同样的，\(\sum\limits_{a,b}\)可以看作是\(\sum\limits_a\sum\limits_b\).事实上，从for型循环的角度来看，\(\sum\)实际上是提供了一个计算的环境，\(\sum\limits_a\)为变量a提供了计算环境，故a不能直接提到求和号的外部，而这个a的求和环境对b不会造成任何影响，可以将b提到求和号的外部
• 乘法对加法的分配律：小学初学乘法分配率的时候，多以\(c(a+b)=ca+cb\)的形式出现，我们了解到乘数\(c\)对和式是怎样的作用效果；但反过来\(ca+cb=c(a+b)\)，意味着多个加数有公共的因子（所谓公共即加数在变但因子不变，因子与加数的变化无关），我们可以把这个公共部分拿到求和号外面来，例如\(\sum\limits_{a}f( c)g(a)=f( c)\sum\limits_a g(a)\)，与上述”环境说“相一致

有时候，我们会遇到形如”加括号”的操作，即\(\sum\sum=(\sum)(\sum)\).事实上，这是由于第二个求和号及其求和对象与第一个求和号无关，将其作为一个整体提出；从提供环境的角度来看，前一个求和号无法为后一个求和号提供环境，二者互不干扰，我们简单的利用括号隔开它们，这与提公因式在形式上是一致的

所谓的大型计算的化简，基本上是不断的对因子进行拆分合并，对求和式进行拆分合并，提出或放入不同的因子，以得到一个相对简洁的形式；如果算不下去了，就再交换一下求和顺序。

变量消除法

概述中，我们提到所有这些算法都是在变量消除法的基础上进行的，所有我们先结合具体实例，对变量消除法进行讨论。

例如上面这个贝叶斯网络，我们想知道边缘概率\(p(d)\).

出于讨论的方便起见，我们假设\(a,b,c,d\)均为离散的二值随机变量，取值集合为\(\{0,1\}\).

利用加法法则与贝叶斯网络的因子分解，我们有 $$ p(d)=\sum_{a,b,c}p(a,b,c,d)=\sum\limits_{a,b,c}p(a)p(b|a)p(c|b)p(d|c) $$ 我们先进行暴力计算。求和号\(\sum\limits_{a,b,c}\)要求我们提供\(a,b,c\)的求和环境，我们让\(a,b,c\)分别取遍\(\{0,1\}\)，有

\[\begin{array}{l} p(d=0)=p(a=0)p(b=0|a=0)p(c=0|b=0)p(d=0|c=0)+p(a=0)p(b=0|a=0)p(c=1|b=0)p(d=0|c=1)+\\ p(a=0)p(b=1|a=0)p(c=0|b=1)p(d=0|c=0)+p(a=0)p(b=1|a=0)p(c=1|b=1)p(d=0|c=1)+\\ p(a=1)p(b=0|a=1)p(c=0|b=0)p(d=0|c=0)+p(a=1)p(b=0|a=1)p(c=1|b=0)p(d=0|c=1)+\\ p(a=1)p(b=1|a=1)p(c=0|b=1)p(d=0|c=0)+p(a=1)p(b=1|a=1)p(c=1|b=1)p(d=0|c=1)\end{array} \]

\[\begin{array}{l} p(d=1)=p(a=0)p(b=0|a=0)p(c=0|b=0)p(d=1|c=0)+p(a=0)p(b=0|a=0)p(c=1|b=0)p(d=1|c=1)+\\ p(a=0)p(b=1|a=0)p(c=0|b=1)p(d=1|c=0)+p(a=0)p(b=1|a=0)p(c=1|b=1)p(d=1|c=1)+\\ p(a=1)p(b=0|a=1)p(c=0|b=0)p(d=1|c=0)+p(a=1)p(b=0|a=1)p(c=1|b=0)p(d=1|c=1)+\\ p(a=1)p(b=1|a=1)p(c=0|b=1)p(d=1|c=0)+p(a=1)p(b=1|a=1)p(c=1|b=1)p(d=1|c=1)\end{array} \]

共16项，非常繁琐。计算复杂度为\(O(K^p)\)，其中\(K\)为随机变量的取值数，\(p\)为随机变量的维数。

依据概述中提到的乘法对加法的分配律的思想，我们将其化简为

\[\begin{array}{l} \sum\limits_{a,b,c}p(a)p(b|a)p(c|b)p(d|c)=\sum\limits_{c}\sum\limits_{b}\sum\limits_{a}p(a)p(b|a)p(c|b)p(d|c)\\ =\sum\limits_{c}p(d|c)\sum\limits_{b}\sum\limits_{a}p(a)p(b|a)p(c|b)\\ =\sum\limits_{c}p(d|c)\sum\limits_{b}p(c|b)\sum\limits_{a}p(a)p(b|a)\\\end{array} \]

这样，最内层的求和式\(\sum\limits_{a}p(a)p(b|a)\)就只含有变量\(a,b\)，实现了变量消除。

为了使变量消除更为明显，我们作记号\(\phi_x(y)\)，指代通过对变量\(x\)求和后变得与\(x\)无关而成为关于\(y\)的因子，则

\[\begin{array}{l} \sum\limits_{c}p(d|c)\sum\limits_{b}p(c|b)\underbrace{\sum\limits_{a}\overbrace{p(a)}^{\psi_a}\overbrace{p(b|a)}^{\psi_{a,b}}}_{\phi_a(b)}\\ =\sum\limits_{c}p(d|c)\underbrace{\sum\limits_{b}p(c|b)\phi_a(b)}_{\phi_b( c)}\\\end{array} =\sum\limits_{c}p(d|c)\phi_b( c)=\phi_c(d) \]

上面的过程非常直观的反应了我们依次消除\(a,b,c\)的过程。

事实上，我们也可以将\(\sum\limits_{a,b,c}\)拆为\(\sum\limits_{a}\sum\limits_{b}\sum\limits_{c}\)，但此处讲解变量消除法是为下文讲解信念传播而服务，将其拆为\(\sum\limits_{c}\sum\limits_{b}\sum\limits_{a}\)隐含了信念传播算法的思想（由叶子到根）。

比较化简前后的两个式子

\[\begin{array}{l} \sum\limits_{a,b,c}p(a)p(b|a)p(c|b)p(d|c)\\ \sum\limits_{c}p(d|c)\sum\limits_{b}p(c|b)\sum\limits_{a}p(a)p(b|a)\end{array} \]

前者我们需要做\((4-1)*16=48\)次乘法以及\((8-1)*2=14\)次加法来完成最终的计算；而采取后者，我们只需要做\(3*4=12\)次乘法以及\(3*2=6\)次加法来完成最终的计算，计算效率大大提升。

因子图

在进行更加深入的讨论前，我们先引入因子图的概念。

从上文提到的因子分解的角度来看，联合概率可以分解为多个因子的乘积。我们可以直观地将其在图中表达出来：引入因子节点，其与该因子中涉及到的所有变量对应的节点相连。

在这样的观点下，我们可以将联合概率的因子分解形式改写为 $$ f(X)=\prod_{S}f_S(X_S) $$ 其中\(S\)为因子\(f_S\)涉及到的节点集合，\(X_S\)为变量集合。下结合具体例子进行说明。

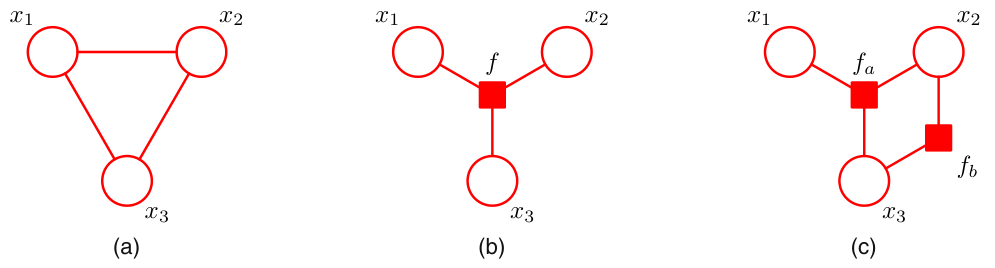
对于图(a)中的马尔可夫随机场，我们可以写出它的因子分解 $$ p(x_1,x_2,x_3)=\frac{1}{Z}\psi_{1,2,3}(x_1,x_2,x_3) $$ 当我们按最大团的形式进行分解时，得到的因子\(\psi_{1,2,3}\)涉及到节点\(1,2,3\)，我们引入因子节点\(f\)代表\(\psi_{1,2,3}\)，与与之相关的节点\(1,2,3\)相连，便得到图(b)中的因子图。

事实上，如果你看过附录中的Hammesley-Clifford定理的证明，你会明白我们其实可以按照从下面的方式来对此马尔可夫随机场进行因子分解 $$ p(x_1,x_2,x_3)=\dfrac{1}{Z}\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{2,3}(x_2,x_3)\psi_{1,2,3}(x_1,x_2,x_3) $$ 调整求积顺序，我们有

\[ p(x_1,x_2,x_3)=\dfrac{1}{Z}\underbrace{\psi_{1,2}(x_1,x_2)\psi_{1,3}(x_1,x_3)\psi_{1,2,3}(x_1,x_2,x_3)}_{f_a(x_1,x_2,x_3)}\underbrace{\psi_{2,3}(x_2,x_3)}_{f_b(x_2,x_3)} \]

这样，我们可以引入两个因子节点\(f_a,f_b\)，让它们分别与相关的节点相连便得到图( c)中的因子图。

请注意，不要混淆因子与团的概念

可见，同一张概率图，由于因子分解形式的不同，会存在多张对应的因子图。因子图只是针对某一种特定的因子分解形式，将对应的因子形象化表达的手段而已。

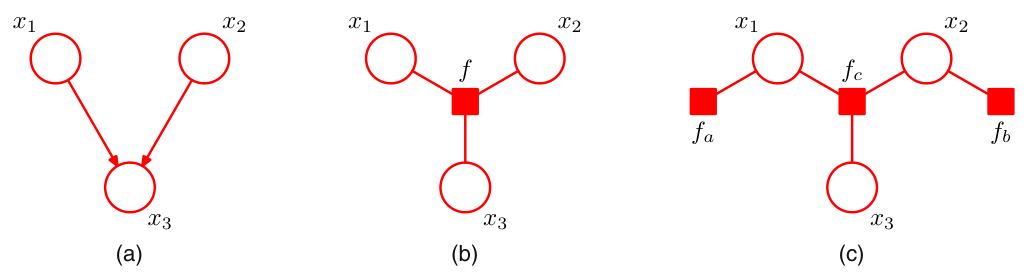
有向图的处理方式完全一致。对于图(a)中的贝叶斯网络，我们写出它的因子分解 $$ p(x_1,x_2,x_3)=p(x_1)p(x_2)p(x_3|x_1,x_2) $$ 如果我们将三项看作一个整体，即

\[ \underbrace{p(x_1)p(x_2)p(x_3|x_1,x_2)}_{f(x_1,x_2,x_3)} \]

那么对应的因子图为图(b).

如果我们将三项看作三个整体，即

\[ \underbrace{p(x_1)}_{f_a(x_1)}\underbrace{p(x_2)}_{f_b(x_2)}\underbrace{p(x_3|x_1,x_2)}_{f_c(x_1,x_2,x_3)} \]

那么对应的因子图为图( c).

可见，即使是同一个因子分解，我们对它的理解不同，一样会产生多种不同的因子图。

在概述中我们提到，基于因子图的Sum-Product算法可以处理道德图中”伦理“过程产生的环结构，原因如下图：

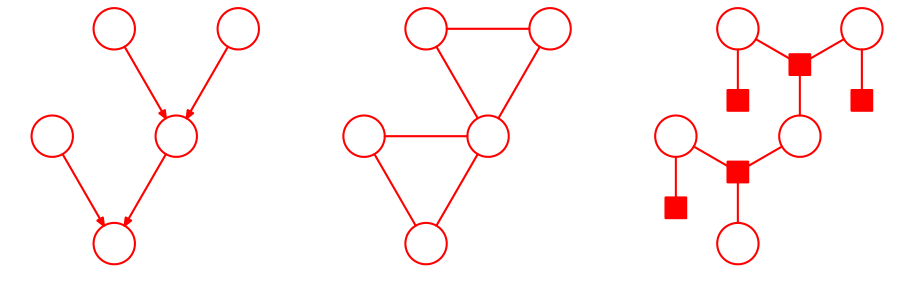
由于”伦理“过程产生的环结构可以被囊括到一个因子中去，所以最终得到的因子图中，环结构将被去除。

除此之外，因子图还存在图结构上的性质：每个因子节点只与变量节点相连，而每个变量节点只与因子节点相连，具有这样性质的图被称为二分图，可以化为如下的形状：

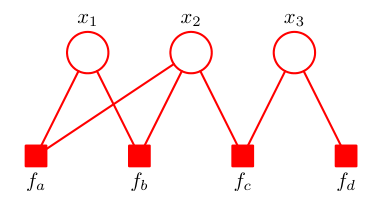
在下面的讨论中，我们并不会利用二分图的性质，而是保持其原有的形态便于直观的读取信息。

算法推导

符号与规定

为了保证行文中符号的一致性，在推导中采取如下的符号体系：

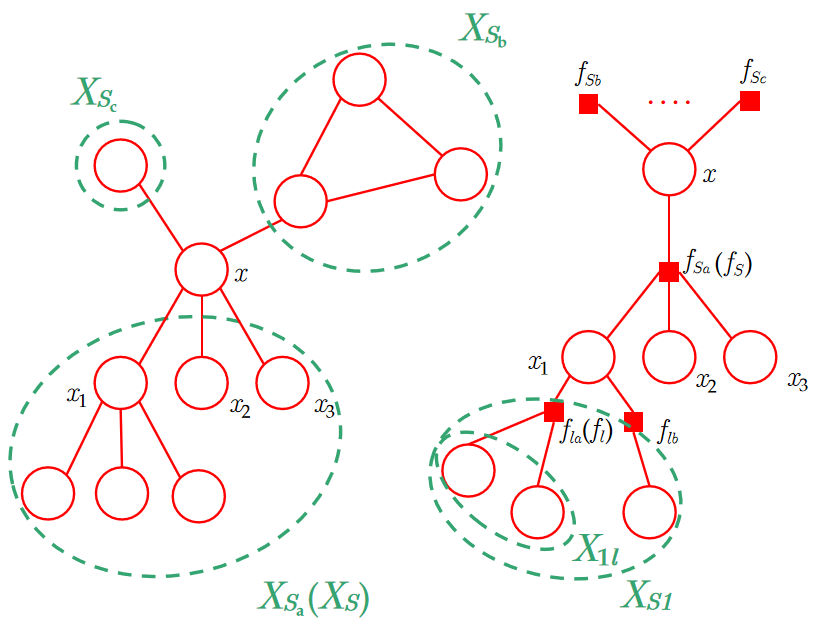
与上文一致地，\(X\)代表全体随机变量，\(x(x_i)\)代表某一随机变量。此处，我们的任务为求变量\(x\)的边缘概率。

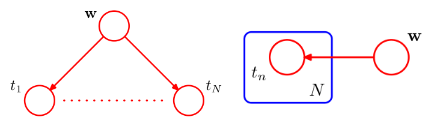
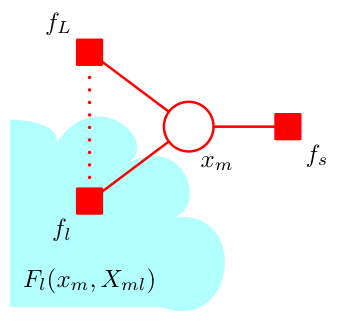
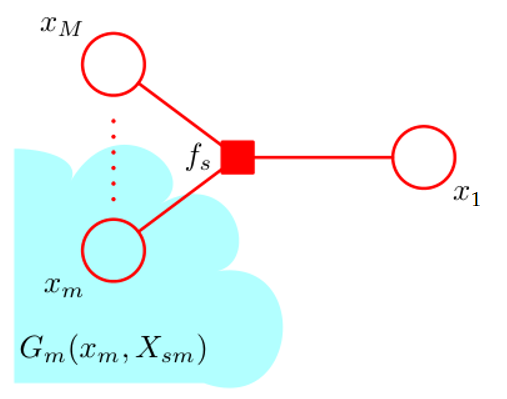
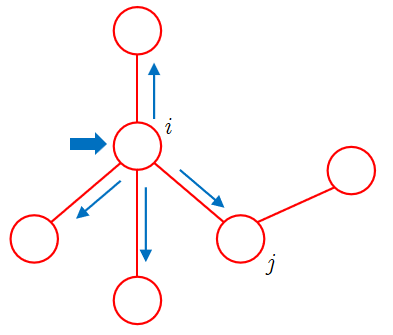
由于算法在具有树结构的因子图上进行，我们考虑每一个与\(x\)相连的因子，\(x\)通过这些因子与图的其它部分相关联。我们记这些因子节点为\(f_{S_a},f_{S_b},\cdots\).一般的，我们将任一\(f_{S_n}\)视作\(f_S\)以简化讨论。于此同时，我们规定\(X_{S_a},X_{S_b},\cdots\)，它们是通过对应因子节点\(f_{S_a},f_{S_b},\cdots\)与\(x\)相连的子树中的所有节点对应的随机变量组成的集合，如图所示。同样的，我们将任一\(X_{S_n}\)视作\(X_S\).

在此基础上我们定义\(x\)关于\(f_S\)的邻居\(x_1,x_2,\cdots,x_M\)，因子\(f_S\)正是定义在\(x\)与它关于\(f_S\)的邻居们构成的集合上的。

进一步地，我们将\(X_S\)中通过邻居节点\(x_m\)与\(f_S\)相连的子树中的所有节点对应的随机变量组成的集合记作\(X_{Sm}\)，如图中的\(X_{S1}\).与刚才定义\(X_S\)时类似，我们在\(x_m\)的基础上定义\(f_l\)与\(X_{ml}\)：与\(x_m\)直接相连的因子节点，除\(f_S\)外，其余因子节点分别记为\(f_{l_a},f_{l_b},\cdots\)，并一般化地记为\(f_l\)；通过\(f_l\)与\(x_m\)相连的子树中的所有节点对应的随机变量的集合记作\(X_{ml}\)。

于此同时，我们用\(ne\)来记邻居构成的集合。对于变量节点\(x_i\)来说，\(ne(x_i)\)是与\(x_i\)相连的所有因子节点的集合；对于因子节点\(f_S\)来说，\(ne(f_S)\)是所有与\(f_S\)相连的变量节点的集合。特别的，当我们说节点集合\(S\in ne(x_i)\)时，\(S\)实际上指的是上文中规定的\(f_S\)对应的\(X_S\)对应的节点集合，即\(S\)是由通过因子节点\(f_S\)与\(x\)相连的子树中的所有节点构成的。

除此之外，我们使用省略号来略去与通过因子节点与讨论对象相连的子树部分。我们还将在变量和变量集合的层面上定义一些函数，如\(F_S\)是由因子节点\(f_S\)关联起来的随机变量在联合概率中的因子之积，具体来说是联合概率中涉及与\(f_S\)对应地\(X_S\)与\(x\)的所有因子；而\(G_m\)是通过\(x_m\)对应的节点（包括\(x_m\)本身）从而与因子节点\(f_S\)关联起来的随机变量在联合概率中的因子之积，具体来说是联合概率中涉及与\(x_m\)对应地\(X_{Sm}\)及\(x_m\)的所有因子；而其余的函数将在具体推导中给出相应的定义。

总结一下，小写字母\(x\)通常代表了随机变量，大写字母\(X\)通常代表了变量集合，而\(X_S\)的下标\(S\)为随机变量集合在图中对应的节点集合，对于函数\(G,F\)，可以简单的通过它们所接受的自变量来判断它们代表了联合概率中的哪一部分因子（\(F\)面向因子节点进行定义，而\(G\)面向变量节点进行定义）。算法的具体推导过程并不是十分复杂，如果忘记了记号的具体含义，可以参照上述图示。

注：

1. 原书中仅通过图示的手段给出了部分记号的含义，容易使读者感到一头雾水；尽管将所有的记号全部给出会给读者带来一定的心理压力，但配合综合图示，在感到困惑时能够有迹可循

2. 或是迫于时间压力，主讲人仅给出了半个算法的部分推导。这里将按照书本顺序将其补全

3. 书中此处采用小写s来指代变量集合，为了与前文风格保持一致，采用了大写S，具体算式可能与书中摘录的图示稍有出入

下文为连续的推导过程，处于简洁考虑，所有式子默认采用\((*)\)标注，式前的\((*)\)默认指上一个式子。

推导过程

先明确我们的目标：求边缘概率\(p(x)\).由加法原理，我们有 $$ p(x)=\sum\limits_{X\setminus x}p(X) $$ 引入因子图中因子分解的概念，我们有 $$ p(X)=\prod\limits_Sf_S(X_S) $$ 此处对因子\(S\)的划分较为自由。结合具体任务，我们选定如下的划分方式 $$ p(X)=\prod\limits_{S\in ne(x)}F_S(x,X_S) $$ 事实上，在上述对\(X_S\)的定义过程中已经蕴含了这种划分的背后的思想。由于算法在具有树结构的因子图上进行，\(x\)通过与之相连的因子节点与整张图其余部分相连；换句话说，对\(\forall S\in ne(x)\)，即\(S\)取遍\(f_{S_a},f_{S_b},\cdots\)时，\(F_S(x,X_S)\)也将取遍联合概率中的所有因子；自然而然地，\(F_S\)定义在\(\{x\}\cup X_S\)上，指代了涉及这些随机变量的因子。

将此处的\(p(X)\)带入边缘概率的表达式，得

\[ p(x)=\sum\limits_{X\setminus x}\prod\limits_{S\in ne(x)}F_S(x,X_S)(*) \]

既然\(S\)能将\(x\)外的节点取遍，我们自然可以利用\(S\)来拆解求和号

\[ (*)=\sum\limits_{X_{S_a}}\sum\limits_{X_{S_b}}\cdots\sum\limits_{X_{S_n}}\prod\limits_{S\in ne(x)}F_S(x,X_S)(*) \]

将累乘写开，利用乘法分配律作进一步的化简

\[\begin{array}{l} (*)=\sum\limits_{X_{S_a}}\sum\limits_{X_{S_b}}\cdots\sum\limits_{X_{S_n}}F_{S_a}(x,X_{S_a})F_{S_b}(x,X_{S_b})\cdots F_{S_n}(x,X_{S_n})\\ =\sum\limits_{X_{S_a}}F_{S_a}(x,X_{S_a})\sum\limits_{X_{S_b}}F_{S_b}(x,X_{S_b})\cdots\sum\limits_{X_{S_n}}F_{S_n}(x,X_{S_n})\\ =\Big[\sum\limits_{X_{S_a}}F_{S_a}(x,X_{S_a})\Big]\Big[\sum\limits_{X_{S_b}}F_{S_b}(x,X_{S_b})\Big]\cdots\Big[\sum\limits_{X_{S_n}}F_{S_n}(x,X_{S_n})\Big]\\ =\prod_{S\in ne(x)}\sum\limits_{X_S}F_S(x,X_S)\end{array} \]

其中最后一步利用累乘符号对结果进行简化。

我们已经得到了一个相对简单的结果，我们作定义

\[ \mu_{f_S\to x}(x)\triangleq\sum\limits_{X_S}F_S(x,X_S) \]

从上述过程中我们可以看出，若应用将乘法分配律的步骤称为变量消除法，那么每一个因式中，\(\mu_{f_S\to x}(x)\)携带了整个式子中与\(f_S\)有关的全部“信息"，通过累乘的方式将它们传递到我们的目标中，如图：

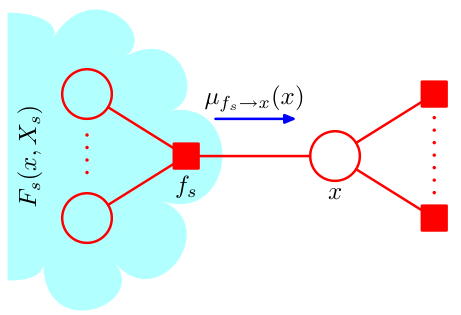
这便是从因子节点到变量节点的”信念传播“。

由于\(F_S\)还可以继续化简，我们将\(F_S\)中的因子展开出来，有 $$ F_S(x,X_S)=f_S(x_1,x_2,\dots,x_M)G_1(x_1,X_{S1})G_2(x_2,X_{S2})\cdots G_M(x_M,X_{SM}) $$ 从定义的图示中我们能很明显看出它的正确性：\(F_S(x,X_S)\)囊括了\(\{x\}\cup X_S\)对应的节点，这些节点包括了\(f_S\)本身涵盖的节点（即\(x\)与\(x\)关于\(f_S\)的邻居节点），还有与这些邻居节点相连的子树部分。由于条件独立性的存在，在\(\{x\}\cup X_S\)中，\(x\)仅与这些邻居节点有关，而与其余的子树无关，故可将这些子树部分的因子写作对应\(G_m(x_m,X_{SM})\)的乘积。

将上述分解形式带入\(\mu_{f_S\to x}(x)\)得

\[ \mu_{f_S\to x}(x)=\sum\limits_{X_S}f_S(x_1,x_2,\dots,x_M)G_1(x_1,X_{S1})G_2(x_2,X_{S2})\cdots G_M(x_M,X_{SM})(*) \]

根据上述讨论，对\(X_S\)进行拆分 $$ X_S={x_1}\cup{x_2}\cup\cdots\cup{x_M}\cup X_{S1}\cup X_{S2}\cup\cdots\cup X_{SM} $$ 在此基础上利用分配律对原式进行化简

\[\begin{array}{l} (*)=\sum\limits_{x_1}\cdots\sum\limits_{x_M}\sum\limits_{X_{S1}}\cdots\sum\limits_{X_{SM}}f_S(x_1,x_2,\dots,x_M)G_1(x_1,X_{S1})G_2(x_2,X_{S2})\cdots G_M(x_M,X_{SM})\\ =\sum\limits_{x_1}\cdots\sum\limits_{x_M}f_S(x_1,x_2,\dots,x_M)\sum\limits_{X_{S1}}G_1(x_1,X_{S1})\cdots\sum\limits_{X_{SM}}G_M(x_M,X_{SM})\\ =\sum\limits_{x_1}\cdots\sum\limits_{x_M}f_S(x_1,x_2,\dots,x_M)\Big[\sum\limits_{X_{S1}}G_1(x_1,X_{S1})\Big]\cdots\Big[\sum\limits_{X_{SM}}G_M(x_M,X_{SM})\Big]\\ =\sum\limits_{x_1}\cdots\sum\limits_{x_M}f_S(x_1,x_2,\dots,x_M)\prod\limits_{m\in ne(f_S)\setminus \{x\}}\sum\limits_{X_{Sm}}G_m(x_m,X_{Sm})\end{array} \]

其中最后一步用\(ne(f_S)\setminus\{x\}\)对这些\(x\)关于\(f_S\)的邻居进行刻画，从而写作累乘形式以化简。注意，因子\(G_m(x_m,X_{Sm})\)依赖于\(x_m\)，需要\(\sum\limits_{x_m}\)提供的求和环境，故不可以提到前面去。

仿照前面定义\(\mu_{f_S\to x}(x)\)的做法，我们作定义 $$ \mu_{x_m\to f_S}(x_m)\triangleq\sum\limits_{X_{Sm}}G_m(x_m,X_{Sm}) $$ 同样的，我们可以认为\(\mu_{x_m\to f_S}(x_m)\)携带了与之关联的子树\(X_{S_m}\)中的全部信息，如图：

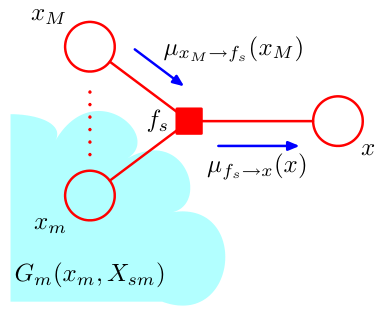
这便是变量节点到因子节点的“信念传播”。结合上述因子节点到变量节点的“信念传播”，从图中我们可以直观的理解这一连续的过程。

继续化简\(G_m(x_m,X_{Sm})\)，不难发现，以\(x_m\)为根的子树的结构，与将\(x\)作为原树根节点的树结构完全一致。仿照前面的划分，我们有 $$ G_m(x_m,X_{Sm})=\prod\limits_{l\in ne(x_m)\setminus f_S}F_l(x_m,X_{ml}) $$ 由于在子树中复现前文的操作，我们需要将\(f_S\)节点从\(ne(x_m)\)中剔除。

同样的，将上述分解形式带入\(\mu_{x_m\to f_S}(x_m)\)得

\[ \mu_{x_m\to f_S}(x_m)=\sum\limits_{X_{Sm}}\prod\limits_{l\in ne(x_m)\setminus f_S}F_l(x_m,X_{ml})(*) \]

同样的，我们利用\(l\)来拆分求和号，并将累乘写开

\[\begin{array}{l} (*)=\sum\limits_{X_{l_a}}\sum\limits_{X_{l_b}}\cdots\sum\limits_{X_{l_n}}\prod\limits_{l\in ne(x_m)\setminus f_S}F_l(x_m,X_{ml})\\ =\sum\limits_{X_{l_a}}\sum\limits_{X_{l_b}}\cdots\sum\limits_{X_{l_n}}F_{l_a}(x_m,X_{ml_a})F_{l_b}(x_m,X_{ml_b})\cdots F_{l_n}(x_m,X_{ml_n})\\ =\sum\limits_{X_{l_a}}F_{l_a}(x_m,X_{ml_a})\sum\limits_{X_{l_b}}F_{l_b}(x_m,X_{ml_b})\cdots\sum\limits_{X_{l_n}} F_{l_n}(x_m,X_{ml_n})\\ =\Big[\sum\limits_{X_{l_a}}F_{l_a}(x_m,X_{ml_a})\Big]\Big[\sum\limits_{X_{l_b}}F_{l_b}(x_m,X_{ml_b})\Big]\cdots\Big[\sum\limits_{X_{l_n}} F_{l_n}(x_m,X_{ml_n})\Big]\\ =\prod\limits_{l\in ne(x_m)\setminus f_S}\sum\limits_{X_l} F_l(x_m,X_{ml})=\prod\limits_{l\in ne(x_m)\setminus f_S}\mu_{f_l\to x_m}(x_m) \end{array}\]

最后同样利用累乘将其合并，而累乘的对象正是上文定义的因子节点到变量节点“信念传播”的形式。上述推导过程如图所示：

至此，Sum-Product算法的主体推导完成。下面对边界进行讨论：

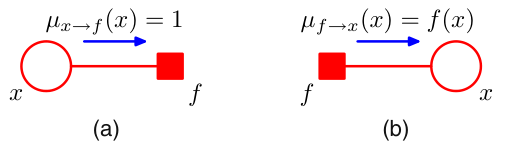
直接带入上述推导结果，不难得出，对于叶型随机变量节点，\(\mu_{x\to f}(x)=1\)，而对于叶型因子节点，\(\mu_{f\to x}(x)=f(x)\).

Sum-Product算法总结如下：

\[\begin{array}{l} \left\{\begin{array}{ll} p(x)=\prod\limits_{S\in ne(x)}\mu_{f_S\to x}(x)\\ \mu_{f\to x}(x)=\sum\limits_{x_1,\cdots,x_M}f(x,x_1,\cdots,x_M)\prod\limits_{m\in ne(f)\setminus x}\mu_{x_m\to f}(x_m)\\ \mu_{x\to f}(x)=\prod\limits_{l\in ne(x)\setminus f}\mu_{f_l\to x}(x) \end{array}\right.\end{array} \]

在推导过程中，我们并没有考虑到归一化的问题。事实上，我们可以通过对其中任意一个随机变量进行归一化，从而得到整体共用的归一化常数。

实例

下用实例来验证Sum-Product算法的正确性。

在利用算法进行具体操作时，我们随机选定根节点，既可以时变量节点，又可以是因子节点。从根节点出发，我们先递后归求出所有\(\mu_{f_S\to x}\)与\(\mu_{x_m\to f_S}\)；利用上面总结中的第一条，我们可以利用这些“信息”表达出所有的边缘概率。

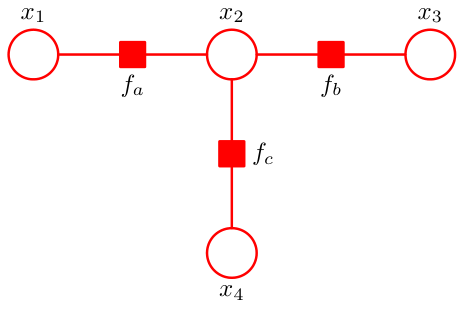
如图，根据因子图的形式，我们写出它联合概率的因子分解 $$ \tilde{p}(X)=f_a(x_1,x_2)f_b(x_2,x_3)f_c(x_2,x_4) $$ 这里，我们使用\(\tilde{p}\)来指代未归一化的概率。

我们的目的是求解\(\tilde{p}(x_2)\).

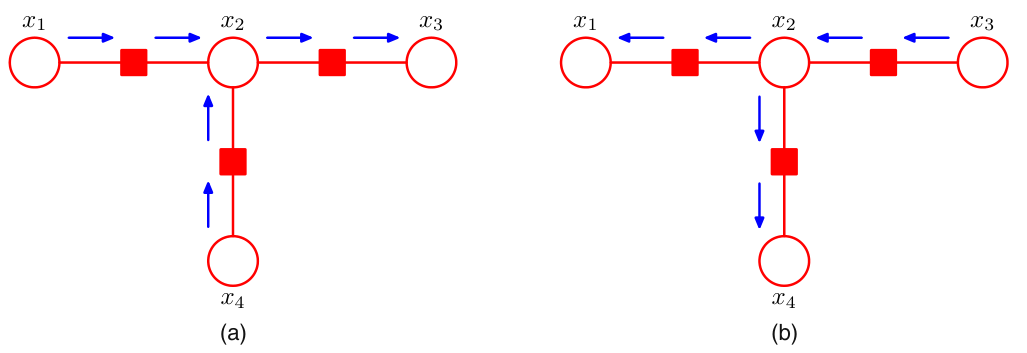
现选定\(x_3\)作根节点，分别从叶子向根、从根向叶子写出全部的信息：

图(a)：叶子\(\to\)根

\[\begin{array}{l} \mu_{x_1\to f_a}(x_1)=1\\ \mu_{f_a\to x_2}(x_2)=\sum\limits_{x_1}f_a(x_1,x_2)\\ \mu_{x_4\to f_c}(x_4)=1\\ \mu_{f_c\to x_2}(x_2)=\sum\limits_{x_4}f_c(x_2,x_4)\\ \mu_{x_2\to f_b}(x_2)=\mu_{f_a\to x_2}(x_2)\mu_{f_c\to x_2}(x_2)\\ \mu_{f_b\to x_3}(x_3)=\sum\limits_{x_2}f_b(x_2,x_3)\mu_{x_2\to f_b}(x_2)\end{array} \]

图(b)：根\(\to\)叶子

\[\begin{array}{l} \mu_{x_3\to f_b}(x_3)=1\\ \mu_{f_b\to x_2}(x_2)=\sum\limits_{x_3}f_b(x_2,x_3)\\ \mu_{x_2\to f_a}(x_2)=\mu_{f_b\to x_2}(x_2)\mu_{f_c\to x_2}(x_2)\\ \mu_{f_a\to x_1}(x_1)=\sum\limits_{x_2}f_a(x_1,x_2)\mu_{x_2\to f_a}(x_2)\\ \mu_{x_2\to f_c}(x_2)=\mu_{f_a\to x_2}(x_2)\mu_{f_b\to x_2}(x_2)\\ \mu_{f_c\to x_4}(x_4)=\sum\limits_{x_2}f_c(x_2,x_4)\mu_{x_2\to f_c}(x_2)\end{array} \]

注：按叶子到根的顺序能够保证其中的每个节点在向下继续传递信息前，能够收集到足够的信息；而从根到叶子的传递过程中，根成了唯一的信息源，故需要利用先前叶子传递到根的信息，所里两个步骤具有先后顺序

在此基础上，我们得到

\[\begin{array}{l} \tilde{p}(x_2)=\mu_{f_a\to x_2}(x_2)\mu_{f_b\to x_2}(x_2)\mu_{f_c\to x_2}(x_2)\\ =\sum\limits_{x_1}f_a(x_1,x_2)\sum\limits_{x_3}f_b(x_2,x_3)\sum\limits_{x_4}f_c(x_2,x_4)\end{array} \]

而纯粹利用变量消除法，我们有

\[\begin{array}{l} \tilde{p}(x_2)=\sum\limits_{x_1,x_3,x_4}p(X)\\ =\sum\limits_{x_1}\sum\limits_{x_3}\sum\limits_{x_4}f_a(x_1,x_2)f_b(x_2,x_3)f_c(x_2,x_4)\\ =\sum\limits_{x_1}f_a(x_1,x_2)\sum\limits_{x_3}f_b(x_2,x_3)\sum\limits_{x_4}f_c(x_2,x_4)\end{array} \]

二者结果一致，即验证了Sum-Product算法的正确性。

衍生算法

回到我们的推断任务上来，我们需要解决边缘概率、条件概率与最大后验三个问题。利用上述的Sum-Product算法，我们已经能够高效地完成第一个任务——求边缘概率。

而对于求解条件概率，利用贝叶斯法则，我们有 $$ p(X_A|X_B)=\dfrac{p(X_A,X_B)}{p(X_B)} $$ 我们不再是求单个变量的边缘概率，而是求解变量集合的边缘概率。

求解随机变量集合的边缘概率

如图，与上文处理\(F_S(x,X_S)\)时采取的手法一致地，我们将联合概率拆解为 $$ p(X)=f_S(X_S)\prod\limits_{m\in ne(f_S)}G_m(x_m,X_{Sm}) $$

这里的\(X_S\)与上文中的含义略有不同，此处指\(f_S\)关联起来的目标变量集合

利用加法法则，我们有

\[\begin{array}{l} p(X_S)=\sum\limits_{X\setminus X_S}p(X)\\ =\sum\limits_{X\setminus X_S}f_S(X_S)\prod\limits_{m\in ne(f_S)}G_m(x_m,X_{Sm})\\ =f_S(X_S)\sum\limits_{X\setminus X_S}\prod\limits_{m\in ne(f_S)}G_m(x_m,X_{Sm})(*)\end{array} \]

同样的，我们对\(X\setminus X_S\)有如下拆分 $$ X\setminus X_S = X_{S1}\cup X_{S2}\cup\cdots\cup X_{SM}=\bigcup\limits_{i\in ne(f_S)}X_{Si} $$ 利用上述结果将求和号打开

\[\begin{array}{l} (*)=f_S(X_S)\sum\limits_{X_{S1}}\cdots\sum\limits_{X_{SM}}G_1(x_1,X_{S1})\cdots G_M(x_M,X_{SM})\\ =f_S(X_S)\sum\limits_{X_{S1}}G_1(x_1,X_{S1})\cdots\sum\limits_{X_{SM}}G_M(x_M,X_{SM})\\ =f_S(X_S)\Big[\sum\limits_{X_{S1}}G_1(x_1,X_{S1})\Big]\cdots\Big[\sum\limits_{X_{SM}}G_M(x_M,X_{SM})\Big]\\ =f_S(X_S)\prod_{i\in ne(f_S)}\sum_{X_{Si}}G_i(x_i,X_{Si})\end{array} \]

最后，根据\(\mu_{x\to f}(x)\)的定义，我们最终得到 $$ p(X_S)=f_S(X_S)\prod\limits_{i\in ne(f_S)}\mu_{x_i\to f_S}(x_i) $$ 这样，我们可以利用Sum-Product得到的信息求得随机变量集合的边缘概率。

观测变量处理

上述讨论中，我们默认所有变量都是未观测变量，而对于观测变量来说，只需对联合概率作小小的改进即可胜任。

假设\(X=h\cup v\)，其中\(h\)为隐变量，\(v\)为观测变量，且观测值为\(\hat v\).我们向联合概率中引入一些因子，得到 $$ p(h,v=\hat v)=p(X)\prod\limits_iI(v_i,\hat{v_i}) $$ 其中，

\[ I(v,\hat v)= \left\{ \begin{array}{ll} 1,&v=\hat v,\\ 0,&v\not=\hat v. \end{array} \right. \]

求最大后验

即要求\(X^{max}=\mathop{\arg\max}\limits_X\ p(X)\).

我们先考虑一个稍微弱化的任务：不求出联合概率最大时变量的具体取值，而是求出对应的最大概率，即 $$ p(X^{max})=\max\limits_{X}p(X) $$ 事实上，\(max\)与\(\sum\)一样，是可以拆解的。我们想求三个数的最大值，可以先求出其中两个数的最大值，再与第三数进行比较。

因此，我们有 $$ \max\limits_{X}p(X)=\max\limits_{x_1}\max\limits_{x_2}\cdots\max\limits_{x_3}p(X) $$ 同样的，乘法关于最大值的分配律依然成立，即\(c\cdot \max(a,b)=\max(ca,cb)\).既然如此，我们依旧可以用理解\(\sum\)的方式来理解\(\max\).而针对最大后验值，从形式上来说，与求解某一变量的边缘概率几乎一致，只不过求边缘概率时不需要对所求的目标变量求和，故求最大后验时会多一层\(\max\)。

将Sum-Product算法的\(\sum\)改写为\(\max\)，就得到了所谓的Max-Product算法，即

\[ \left\{\begin{array}{ll} \max\limits_{X}p(X)=\max\limits_{x}\prod\limits_{S\in ne(x)}\mu_{f_S\to x}(x)\\ \mu_{f\to x}(x)=\max\limits_{x_1,\cdots,x_M}f(x,x_1,\cdots,x_M)\prod\limits_{m\in ne(f)\setminus x}\mu_{x_m\to f}(x_m)\\ \mu_{x\to f}(x)=\prod\limits_{l\in ne(x)\setminus f}\mu_{f_l\to x}(x) \end{array}\right. \]

同样的，我们选定一个根节点，并且只需要将信息从叶子传递到根即可；最后，针对\(x\)的不同取值求出其最大值，即为最大后验的值。

整个求解过程是一个动态规划(Dynamic Programming)，我们通过不断的对部分随机变量进行优化，最终得到全局的最优解。

同样的，我们可以利用动态规划中的常见的反向追踪(back-tracking)手法来求得\(X^{max}\).在每次进行从当前最优化的\(x_{n-1}^{max}\)到\(x_n\)状态转移时，我们都记录下它的来源，记 $$ \phi(x_n)=x_{n-1}^{\max} $$ 这样，在我们求得最后根节点\(x^{max}\)后，将它带到\(\phi\)中，就可以找出\(X^{max}\)的具体取值了，如下图：

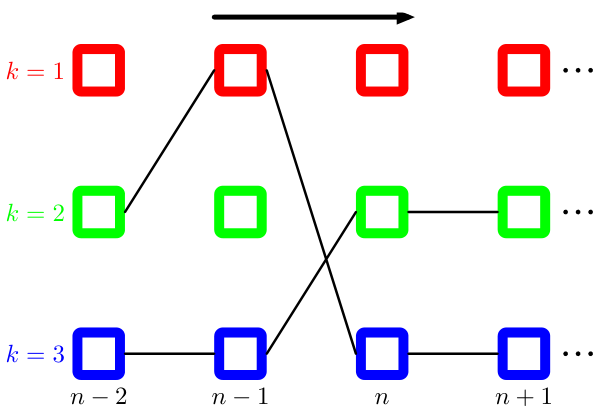
但Max-Product算法还有优化的空间。不难看出，我们对这些因子进行了多次乘法，而这些因子是联合概率的组成部分。实际应用中，对一个小于1的浮点数进行多次乘法，对精度构成了挑战，而简单的取一个对数便能将乘法化为加法，完美的解决问题，如下

\[ \left\{\begin{array}{ll} \ln\max\limits_{X}p(X)=\max\limits_{x}\Big[\sum\limits_{S\in ne(x)}\mu_{f_S\to x}(x)\Big]\\ \mu_{f\to x}(x)=\max\limits_{x_1,\cdots,x_M}\Big[\ln f(x,x_1,\cdots,x_M)+\sum\limits_{m\in ne(f)\setminus x}\mu_{x_m\to f}(x_m)\Big]\\ \mu_{x\to f}(x)=\sum\limits_{l\in ne(x)\setminus f}\mu_{f_l\to x}(x) \end{array}\right. \]

具体地，我们取\(\phi(x_n)\)为 $$ \phi(x_n)=\mathop{\arg\max}\limits_{x_{n-1}}[\ln f_{n-1,n}(x_{n-1},x_n)+\mu_{x_{n-1}\to f_{n-1,n}}(x_n)] $$ 相应地，边界条件也发生了改变 $$ \mu_{x\to f}(x)=0,\mu_{f\to x}(x)=\ln f(x) $$ Max-Product(Max-Sum)算法可以看作是对Viterbi算法的推广。

后续内容书中点到为止，此处亦不做具体展开。

附录

Hammesley-Clifford定理证明

Hammesley-Clifford定理： $$ MRF\Leftrightarrow Gibbs $$

定义

定义1 MRF $$ p(x_i|X\setminus {x_i})=p(x_i|ne_i) $$ 定义2 Gibbs $$ p(X)=\dfrac{1}{Z}\prod\limits_C \psi_C(X_C)\ Z=\sum\limits_X\prod\limits_C\psi_C(X_C) $$

注：

1. 这里给出了马尔可夫随机场(Markov Random Field,MRF)和吉布斯分布(Gibbs)的定义

2. 由于马尔可夫随机场的三条马尔可夫性等价，这里选取的是局部马尔可夫性，即\(x_i\perp\!\!\!\perp X\setminus (x_i\cup ne_i)|ne_i\)，在此基础上，由于二者的独立，可以得到： $$ p(x_i|ne_i)=p(x_i|ne_i,X\setminus (x_i\cup ne_i))=p(x_i|X\setminus {x_i}) $$

3. 此处吉布斯分布的因子分解中，\(C\)指团（不一定是最大团）

记号与说明：

• 下文对变量集合与节点集合做符号上的区分：\(X\)指全体随机变量，\(G\)指图的全部节点，但不对变量与节点做符号上的区分，\(x_i\)即可以指随机变量\(x_i\)，又可以指随机变量对应的节点；同时记所有团的集合为\(C_G\).

• 下文中，将所有随机变量当作离散型随机变量处理。对于连续性随机变量，将\(\sum\)替换为\(\int\)即可。

• 由于下文为连续的推导过程，处于简洁考虑，所有式子默认采用\((*)\)标注，式前的\((*)\)默认指上一个式子。

Gibbs\(\Rightarrow\)MRF

只要证\(p(x_i|ne_i)=p(x_i|X\setminus \{x_i\})\).

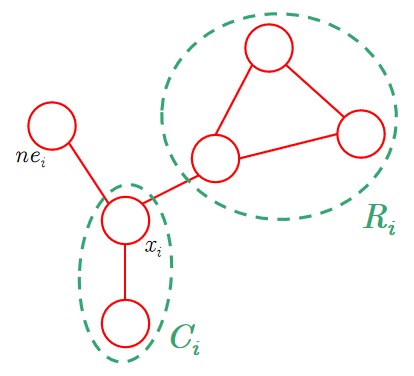
记\(D_i\triangleq ne_i\cup x_i\)（此处指节点集合），则由贝叶斯法则和加法法则得： $$ p(x_i|ne_i)=\dfrac{p(x_i,ne_i)}{p(ne_i)}=\dfrac{\sum\limits_{G\setminus D_i}p(X)}{\sum\limits_{G\setminus ne_i}p(X)}(*) $$ 由定义知，\(G\setminus ne_i=G\setminus (D_i\setminus \{x_i\})={x_i}\cup(G\setminus D_i)\)，因此\(\sum\limits_{G\setminus ne_i}\)可写作\(\sum\limits_{x_i}\sum\limits_{G\setminus D_i}\).

再带入Gibbs中\(p(X)\)的表达，得：

\[(*)=\dfrac{\sum\limits_{G\setminus D_i}p(X)}{\sum\limits_{x_i}\sum\limits_{G\setminus D_i}p(X)}=\dfrac{\sum\limits_{G\setminus D_i}\prod\limits_{C\in C_G}\psi_C(X_C)}{\sum\limits_{x_i}\sum\limits_{G\setminus D_i}\prod\limits_{C\in C_G}\psi_C(X_C)}(*)\]

如图，我们将\(C_G\)按照是否含有\(x_i\)进行分组，记 $$ C_i\triangleq{C|C\in C_G,x_i\in C},R_i\triangleq{C|C\in C_G,x_i\notin C} $$ 则 $$ \prod\limits_{C\in C_G}\psi_C(X_C)=\prod\limits_{C\in C_i}\psi_C(X_C)\prod\limits_{C\in R_i}\psi_C(X_C) $$ 可以证明：\(\forall x\in C_i,x\notin G\setminus D_i\)，即\(C_i\)内的节点与\(G\)中\(D_i\)外的节点无关。

只要证\(\forall x\in C_i,x\in D_i\).根据团的定义，团内节点两两相连。又\(x_i\in C_i\)，则\(\forall x\in C_i(x\not=x_i)\)，\(x\)与\(x_i\)直接相连。

根据\(ne_i\)的定义，与\(x_i\)直接相连的节点都是\(x_i\)的邻居。则\(x\in ne_i\).又\(ne_i\subset D_i\)，所以\(x\in D_i\).当\(x=x_i\)时，\(x_i\in D_i\)也符合。即证。

因此，\(C_i\)与\(G\setminus D_i\)无关，因子\(\prod\limits_{C\in C_i}\psi_C(X_C)\)可以提到\(\sum\limits_{G\setminus D_i}\)外，同时，\(R_i\)与\(x_i\)无关，可将其提到\(\sum\limits_{x_i}\)外，得：

\[\begin{array}{l} (*)=\dfrac{\sum\limits_{G\setminus D_i}\prod\limits_{C\in C_i}\psi_C(X_C)\prod\limits_{C\in R_i}\psi_C(X_C)}{\sum\limits_{x_i}\sum\limits_{G\setminus D_i}\prod\limits_{C\in C_i}\psi_C(X_C)\prod\limits_{C\in R_i}\psi_C(X_C)}\\ =\dfrac{\prod\limits_{C\in C_i}\psi_C(X_C)\sum\limits_{G\setminus D_i}\prod\limits_{C\in R_i}\psi_C(X_C)}{\sum\limits_{x_i}\prod\limits_{C\in C_i}\psi_C(X_C)\sum\limits_{G\setminus D_i}\prod\limits_{C\in R_i}\psi_C(X_C)}\\ =\dfrac{\prod\limits_{C\in C_i}\psi_C(X_C)\sum\limits_{G\setminus D_i}\prod\limits_{C\in R_i}\psi_C(X_C)}{\Big[\sum\limits_{G\setminus D_i}\prod\limits_{C\in R_i}\psi_C(X_C)\Big]\Big[\sum\limits_{x_i}\prod\limits_{C\in C_i}\psi_C(X_C)\Big]}\\ =\dfrac{\prod\limits_{C\in C_i}\psi_C(X_C)}{\sum\limits_{x_i}\prod\limits_{C\in C_i}\psi_C(X_C)}(*)\end{array} \]

其中最后一步进行了约分。

为了得到目标的形式，向分子分母同乘\(\prod\limits_{C\in R_i}\psi_C(X_C)\)得：

\[\begin{array}{l} (*)=\dfrac{\prod\limits_{C\in C_i}\psi_C(X_C)\prod\limits_{C\in R_i}\psi_C(X_C)}{\sum\limits_{x_i}\prod\limits_{C\in C_i}\psi_C(X_C)\prod\limits_{C\in R_i}\psi_C(X_C)}\\ =\dfrac{\prod\limits_{C\in C_G}\psi_C(X_C)}{\sum\limits_{x_i}\prod\limits_{C\in C_G}\psi_C(X_C)} =\dfrac{p(X)}{\sum\limits_{x_i}p(X)}\\ =\dfrac{p(X)}{p(X\setminus\{x_i\})}=\dfrac{p(X\setminus\{x_i\})p(x_i|X\setminus\{x_i\})}{p(X\setminus\{x_i\})}=p(x_i|X\setminus\{x_i\}) \end{array}\]

其中最后两步分别运用加法法则和乘法法则。

综上，即证Gibbs\(\Rightarrow\)MRF。

MRF\(\Rightarrow\)Gibbs

\(\forall S\subset G\)，构造 $$ f_S(X_S)=\prod\limits_{Z\subset S}p(Z=X_Z,G\setminus Z=0)^{(-1)^{|S|-|Z|}} $$ 其中\(Z\)为\(S\)的子集。

注：

1. \(f_S\)定义在节点集合\(S\)对应的变量集合\(X_S\)上
2. \(p(Z=X_Z,G\setminus Z=0)\)的含义是图中仅\(Z\)中节点对应的随机变量取到对应（\(X_S\)中的）\(X_Z\)部分的值，而其余变量取0（默认值）时的概率

由于\(Z\subset S\)，故\(|Z|\leqslant|S|\)；当\(|Z|=|S|\)时，\(f_S(X_S)=p(S=X_S,G\setminus S=0)\).

只要证：(1)\(\prod\limits_{S\subset G}f_S(X_S)=p(X)\) (2)若\(S\)不是团，则\(f_S(X_S)=1\)

先证(1)，只要证\(\prod\limits_{S\subset G}f_S(X_S)\)中除项\(p(X)\)外其余都可以互相抵消。

原求积顺序是考虑集合\(S\)的全部子集。让我们更换求积顺序，考虑集合\(Z\)的全部母集。

事实上，由于\(p(Z=X_Z,G\setminus Z=0)\)只与\(Z\)有关，当\(Z\)确定后，\(p(Z=X_Z,G\setminus Z=0)\)也就唯一确定了。

对\(\forall Z\subset G\)，记\(\Delta=p(Z=X_Z,G\setminus Z=0)\).下考虑\(Z\)的所有母集\(S\).

当\(S=Z\)时，\(\Delta^{(-1)^0}=\Delta\)

当\(S=Z\cup\{x_i\}(x_i\in G\setminus Z)\)时，\(\Delta^{(-1)^1}=\Delta^{-1}\)，共\(C_{|G|-|Z|}^{1}\)项，故总贡献为\(\Delta^{(-1)C_{|G|-|Z|}^{1}}\)

当\(S=Z\cup\{x_i\}\cup\{x_j\}((x_i,x_j\in G\setminus Z))\)时，\(\Delta^{(-1)^2}=\Delta\)，共\(C_{|G|-|Z|}^{2}\)项

以此类推，\(Z\)对结果的总贡献为： $$ \Delta\Delta^{(-1)C_{|G|-|Z|}^{1}}\Delta^{(-1)^2C_{|G|-|Z|}^{2}}\cdots\Delta^{(-1)^{|G|-|Z|}C_{|G|-|Z|}^{|G|-|Z|}}=\Delta^{C_{|G|-|Z|}^{0}-C_{|G|-|Z|}^{1}+C_{|G|-|Z|}^{2}-\cdots+(-1)^{|G|-|Z|}C_{|G|-|Z|}^{|G|-|Z|}}(*) $$ 由二项式定理知， $$ 0=(1-1)^k=C_k^0-C_k^1+C_k^2-\cdots+(-1)^kC_k^k(k>0) $$ 因此，当\(|Z|<|G|\)时，贡献为\(\Delta^{0}=1\)；当\(|Z|=|G|\)时，贡献为\(\Delta_{\{Z=G\}}\).

所以\(\prod\limits_{S\subset G}f_S(X_S)=\Delta_{\{Z=G\}}=p(X_G)=p(X)\)，即证。

再证(2).

先对条件进行转化。若\(S\)不是团，对团的定义取反，得\(\exists a,b\in S\)，\(a,b\)不直接相连。

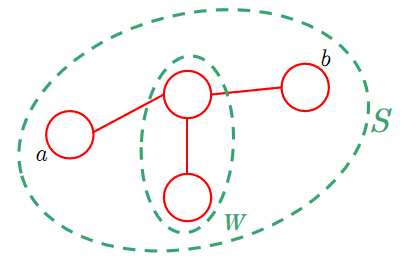
利用这一性质，将\(S\)划分为\(\{a\}\cup\{b\}\cup (S\setminus \{a,b\})\).原求积对象为\(\forall Z\subset S\)，现考虑\(\forall W\subset S\setminus\{a,b\}\)，则由一个\(W\)可以衍生出四个不同的\(S\)：\(W,W\cup\{a\},W\cup\{b\},W\cup\{a,b\}\)，且不同的\(W\)衍生出的\(S\)各不相同。

故\(p(Z=X_Z,G\setminus Z=0)^{(-1)^{|S|-|Z|}}\)可化为以下四项乘积：

\[\begin{array}{l} p(W=X_W,G\setminus W=0)^{(-1)^{|S|-|W|}}\quad(1)\\ p(W\cup\{a\}=X_W\cup\{x_a\},G\setminus (W\cup\{a\})=0)^{(-1)^{|S|-(|W|+1)}}\quad(2)\\ p(W\cup\{b\}=X_W\cup\{x_b\},G\setminus (W\cup\{b\})=0)^{(-1)^{|S|-(|W|+1)}}\quad(3)\\ p(W\cup\{a,b\}=X_W\cup\{x_a,x_b\},G\setminus (W\cup\{a,b\})=0)^{(-1)^{|S|-(|W|+2)}}\quad(4)\end{array} \]

观察一下四项的指数，可以发现式\((1)\)与式\((4)\)指数相等，为\((-1)^{|S|-|W|}\)，而式\((2)\)式\((3)\)指数相等，为\(-(-1)^{|S|-|W|}\).将指数部分\((-1)^{|S|-|W|}\)提出后，式\((2),(3)\)将多出\(-1\)次幂，带上\(-1\)次幂后变为分母。

提出指数部分\((-1)^{|S|-|W|}\)后，四项乘积化为：

\[ \Big[\dfrac{p(W=X_W,G\setminus W=0)p(W\cup\{a,b\}=X_W\cup\{x_a,x_b\},G\setminus (W\cup\{a,b\})=0)}{p(W\cup\{a\}=X_W\cup\{x_a\},G\setminus (W\cup\{a\})=0)p(W\cup\{b\}=X_W\cup\{x_b\},G\setminus (W\cup\{b\})=0)}\Big]^{(-1)^{|S|-|W|}}(*) \]

故原式化为

\[ f_S(X_S)=\prod\limits_{Z\subset S}p(Z=X_Z,G\setminus Z=0)^{(-1)^{|S|-|Z|}}=\prod\limits_{W\subset S\setminus\{a,b\}}\Big(*\Big) \]

要证\(f_S(X_S)=1\),只要证\((*)\equiv 1\)即可。事实上，由于指数的取值仅有\(\{1,-1\}\)，故只要证

\[ \dfrac{p(W=X_W,G\setminus W=0)p(W\cup\{a,b\}=X_W\cup\{x_a,x_b\},G\setminus (W\cup\{a,b\})=0)}{p(W\cup\{a\}=X_W\cup\{x_a\},G\setminus (W\cup\{a\})=0)p(W\cup\{b\}=X_W\cup\{x_b\},G\setminus (W\cup\{b\})=0)}=1 \]

由于a,b为不直接相连的节点，为了利用\(MRF\)中的成对马尔可夫性，我们将上式分组，只要证

\[ \dfrac{p(W=X_W,G\setminus W=0)}{p(W\cup\{a\}=X_W\cup\{x_a\},G\setminus (W\cup\{a\})=0)}=\dfrac{p(W\cup\{b\}=X_W\cup\{x_b\},G\setminus (W\cup\{b\})=0)}{p(W\cup\{a,b\}=X_W\cup\{x_a,x_b\},G\setminus (W\cup\{a,b\})=0)} \]

利用乘法法则对左边进行化简，有

\[ \dfrac{p(W=X_W,G\setminus W=0)}{p(W\cup\{a\}=X_W\cup\{x_a\},G\setminus (W\cup\{a\})=0)}\\ =\dfrac{p(b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)p(a=0|b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)}{p(b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)p(a=x_a|b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)}(*) \]

这一步的实际含义是将状态分子分母中的状态看作由状态\((b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)\)得来。此时\(W\)中的点取到对应值，而\(W\cup\{a,b\}\)外的点取到默认值，并且我们只考虑到让点b取默认值，并未考虑点a所处的状态。

在此基础上，分子的状态是要\(W\)中的点取到对应值，而\(W\)外的点取到默认值。与状态\((b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)\)对比可知，我们还需令点a取到默认值，利用乘法法则对这一步骤进行表达。

类似的，分母要求\(W\)中的点与点a取到对应值，而\(W\)外的点取到默认值。我们还需令点a取到对应值，同样可以利用乘法法则来表达这一步骤。

不难发现，分子分母可以约分，得

\[ (*)=\dfrac{p(a=0|b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)}{p(a=x_a|b=0,W=X_W,G\setminus (W\cup\{a,b\})=0)}(*) \]

在给定的条件下，\(W\cup(G\setminus (W\cup\{a,b\}))=G\setminus\{a,b\}\)中的节点状态都已确定，意味着\(X\setminus\{x_a,x_b\}\)都已被观测，又a,b不直接相连，由成对马尔可夫性知

\[x/_a\perp\!\!\!\perp x_b|X\setminus\{x_a,x_b\}\]

\(x_a,x_b\)互不干扰，我们可以修改条件概率对应条件中节点b的状态而不影响对应的概率值。为了得到目标的形式，我们将点b的状态修改为取到它的对应值，有

\[ (*)=\dfrac{p(a=0|b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)}{p(a=x_a|b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)}(*) \]

继续向目标靠拢，向分子分母同乘\(p(b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)\)，结合乘法法则，有

\[\begin{array}{l} (*)=\dfrac{p(a=0|b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)p(b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)}{p(a=x_a|b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)p(b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)}\\ =\dfrac{p(b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0,a=0)}{p(a=x_a,b=x_b,W=X_W,G\setminus (W\cup\{a,b\})=0)}\\ =\dfrac{p(W\cup\{b\}=X_W\cup\{x_b\},G\setminus (W\cup\{b\})=0)}{p(W\cup\{a,b\}=X_W\cup\{x_a,x_b\},G\setminus (W\cup\{a,b\})=0)} \end{array}\]

综上，即证MRF\(\Rightarrow\)Gibbs。

综合两节内容，定理得证。

讨论

通过上述证明过程，我们会发现两个问题：

(1)Gibbs仅要求势函数定义在团上，并未要求定义在最大团上 (2)推导过程中未见到归一化常数

对于问题(1)，事实上，通过上述讨论，我们发现势函数并不一定要取自最大团。假设现在有团\(C=\{a,b,c\}\)，其所有团的势函数乘积为 $$ \psi_a(a)\psi_b(b)\psi_c( c)\psi_{a,b}(a,b)\psi_{a,c}(a,c)\psi_{b,c}(b,c)\psi_{a,b,c}(a,b,c)\quad(*) $$ 而这些乘积可以看作一个整体\(\Psi_{a,b,c}(a,b,c)=\big(*\big)\).由于已知\(C\)为团，故\(\Psi_{a,b,c}(a,b,c)\)的定义是合理的。另一方面，将上述7项乘积整合在一起，可以大大减少因子的数量，故尽可能取最大团能让计算得到极大的简化。

对于问题(2)，从MRF\(\Rightarrow\)Gibbs的讨论中，我们发现并没有归一化的必要。因为此时我们构造的势函数在累乘后直接得到了联合概率，而联合概率本身是归一化的。

但实际应用中，由于所取的势函数不同，为了保证最终的结果可以用来衡量可能性的大小，我们需要人为的对其进行归一化，使得它能够被看作概率。

非因子形式的Sum-Product算法

引入

让我们继续对变量消除法的讨论。考虑下面的贝叶斯网络：

我们想知道边缘概率\(p(e)\).利用加法法则与贝叶斯网络的因子分解，有

\[\begin{array}{l} p(e)=\sum\limits_{a,b,c,d}p(a,b,c,d,e)\\ =\sum\limits_{a,b,c,d}p(a)p(b|a)p(c|b)p(d|c)p(e|d)(*)\end{array} \]

对其进行变量消除，得

\[\begin{array}{l} (*)=\sum\limits_{d}\sum\limits_{c}\sum\limits_{b}\sum\limits_{a}p(a)p(b|a)p(c|b)p(d|c)p(e|d)\\ =\sum\limits_{d}p(e|d)\sum\limits_{c}p(d|c)\sum\limits_{b}p(c|b)\sum\limits_{a}p(b|a)p(a)\end{array} \]

同时，我们又想知道边缘概率\(p( c)\).重复上述操作，我们有

\[\begin{array}{l} p( c)=\sum\limits_{a,b,d,e}p(a,b,c,d,e)\\ =\sum\limits_{a,b,d,e}p(a)p(b|a)p(c|b)p(d|c)p(e|d)\\ =\sum\limits_{b}p(c|b)\sum\limits_{a}p(b|a)p(a)\sum\limits_{d}p(d|c)\sum\limits_{e}p(e|d)\\ =\Big[\sum\limits_{b}p(c|b)\sum\limits_{a}p(b|a)p(a)\Big]\Big[\sum\limits_{d}p(d|c)\sum\limits_{e}p(e|d)\Big]\end{array} \]

对比上面的计算过程，我们明显的发现，因式\(\sum\limits_{b}p(c|b)\sum\limits_{a}p(b|a)p(a)\)被重复计算了。如果能够重用这些计算结果，将大大提升变量消除法的效率，出于这一目的，我们引入信念传播算法。

符号与规定

为了使传播更加生动形象，针对上文给出的记号\(\phi_x(y)\)，我们使用\(m_{x\to y}(x_y)\)来代替它。我们曾经提到过，默认情况下不区分\(y\)与\(x_y\)，由于下面需对具体变量进行求和，故在此记号中我们显式地将随机变量与它对应的节点区别开。

另外，我们延用上文中的\(\psi_S\)记号，指代在因子分解中涉及变量集合\(X_S\)的那一部分因式。同样的，在这里它并不仅仅指代团上定义的势函数。

在算法推导过程中，我们不特意地考虑归一化常数（随时可能将其忽略），具体处理已在正文中介绍。

算法推导

我们结合具体实例进行推导。有兴趣的读者可以尝试直接证明一般化的结论。

考虑如下的马尔可夫随机场，我们想求得边缘概率\(p(a)\).

写出它的因子分解，有 $$ p(a,b,c,d)=\dfrac{1}{Z}\psi_a(a)\psi_b(b)\psi_c( c)\psi_d(d)\psi_{a,b}(a,b)\psi_{b,c}(b,c)\psi_{b,d}(b,d) $$ 仿照引例的手法进行处理，有

\[\begin{array}{l} p(a)=\sum\limits_{x_b,x_c,x_d}p(a,b,c,d)\\ =\sum\limits_{x_b}\sum\limits_{x_c}\sum\limits_{x_d}\psi_a(a)\psi_b(b)\psi_c( c)\psi_d(d)\psi_{a,b}(a,b)\psi_{b,c}(b,c)\psi_{b,d}(b,d)\\ =\psi_a(a)\sum\limits_{x_b}\psi_b(b)\psi_{a,b}(a,b)\sum\limits_{x_c}\psi_c( c)\psi_{b,c}(b,c)\sum\limits_{x_d}\psi_d(d)\psi_{b,d}(b,d) \end{array}\]

引入\(m_{x\to y}(x_y)\)的记号，得

\[\begin{array}{l} \psi_a(a)\sum\limits_{x_b}\psi_b(b)\psi_{a,b}(a,b)\underbrace{\sum\limits_{x_c}\psi_c( c)\psi_{b,c}(b,c)}_{m_{c\to b}(x_b)}\underbrace{\sum\limits_{x_d}\psi_d(d)\psi_{b,d}(b,d)}_{m_{d\to b}(x_b)}\\ =\psi_a(a)\underbrace{\sum\limits_{x_b}\psi_b(b)\psi_{a,b}(a,b)m_{c\to b}(x_b)m_{d\to b}(x_b)}_{m_{b\to a}(x_a)}=\psi_a(a)m_{b\to a}(x_a) \end{array}\]

上述过程又可写作

\[ \left\{ \begin{array}{ll} m_{b\to a}(x_a)=\sum\limits_{x_b}\psi_b(b)\psi_{a,b}(a,b)m_{c\to b}(x_b)m_{d\to b}(x_b)\\ p(a)=\psi_a(a)m_{b\to a}(x_a) \end{array} \right. \]

从图中不难发现，\(c,d\)节点都是\(b\)节点的邻居。与正文类似的，我们引入记号\(ne(i)\)，代指\(i\)节点的全部邻居节点，这样，上式又可以写作

\[ \left\{ \begin{array}{ll} m_{b\to a}(x_a)=\sum\limits_{x_b}\psi_b(b)\psi_{a,b}(a,b)\prod\limits_{k\in ne(b)\setminus a}m_{k\to b}(x_b)\\ p(a)=\psi_a(a)\prod\limits_{k\in ne(a)}m_{k\to a}(x_a) \end{array} \right. \]

进一步泛化\(a,b\)为\(i,j\)，我们将得到Sum-product算法的最终形式

\[ \left\{ \begin{array}{ll} m_{j\to i}(x_i)=\sum\limits_{x_j}\psi_{i,j}(i,j)\psi_j(j)\prod\limits_{k\in ne(j)\setminus i}m_{k\to j}(x_j)\\ p(x_i)=\psi_i(i)\prod\limits_{k\in ne(i)}m_{k\to i}(x_i) \end{array} \right. \]

同样地，它具有传递的形式，我们可以认为节点\(j\)携带的信息量为 $$ belief(j)=\psi_j(j)\prod\limits_{k\in ne(j)\setminus i}m_{k\to j}(x_j) $$ 文艺地，我们可以称之为\(j\)的“信仰（念）”(belief)，由它自己的信息和孩子们传给它的信息构成；而节点\(j\)所能向节点\(i\)传递的信息\(m_{j\to i}\)为 $$ m_{j\to i}(x_i)=\sum\limits_{x_j}\psi_{i,j}(i,j)belief(j) $$ 这便是信念传播的最终表现。

操作细节

同样地，这种形式的Sum-Product算法只需求出所有的信息，就可以用这些信息组装出所有的边缘概率。

具体而言，这有两种实现模式：

• 串行算法(Sequential Implementation)

初始化：任意选定一个根节点，如图中的节点\(a\).

收集信息：按dfs的形式，递归地收集节点信息，叶子节点为递归边界，如图(a)。伪代码如下：

def collectMsg(x, last):
    for neighbor in ne[x]:
        if neighbor == last:
            continue
        collectMsg(neighbor, x)
    #    
    # Calculate x's message
    #

collectMsg(Root, None)

分发信息：按dfs的形式，递归地分发节点信息，如图(b)。伪代码如下：

def distributeMsg(x, last):
    for neighbor in ne[x]:
        if neighbor == last:
            continue
        #
        # Distribute x's message
        #
        distributeMsg(neighbor, x)

distributeMsg(Root, None)

组装信息：至此，所有信息均完成计算，故所求的边缘概率能够从这些信息中得出

• 并行算法(Parallel Implementation)

如图，我们以点为单位开启线程。当每个线程收集到其它节点发送过来的信息后，便立即将其发送出去。同时借助数据结构来记录更新的时序。可以证明，这个算法是收敛的，最终能够有效地求出所有信息，从而组装出我们想要的边缘概率。

衍生算法

同样地，这种形式的Sum-Product算法有其对应的衍生算法。

与正文思路一致，我们得到非因子形式的Max-Product：

\[ \left\{ \begin{array}{ll} m_{j\to i}(x_i)=\max\limits_{x_j}\psi_{i,j}(i,j)\psi_j(j)\prod\limits_{k\in ne(j)\setminus i}m_{k\to j}(x_j)\\ \max\limits_{X}p(X)=\max\limits_{x_i}\psi_i(i)\prod\limits_{k\in ne(i)}m_{k\to i}(x_i) \end{array} \right. \]

与因子形式的Max-Product相比，有趣的是，此处的信息传递仅涉及对一个变量的最优化。我们通过一个实例来体会这一点。

同样是上文中的马尔可夫随机场，现在我们想求得相应的最大后验。

与因子形式的Max-Product类似，我们只需要进行收集信息的过程，如图所示，有

\[\begin{array}{l} m_{c\to b}(x_b)=\max_{x_c}\psi_c( c)\psi_{b,c}(b,c)\\ m_{d\to b}(x_b)=\max_{x_d}\psi_d(d)\psi_{b,d}(b,d)\\ m_{b\to a}(x_a)=\max\limits_{x_b}\psi_b(b)\psi_{a,b}(a,b)m_{c\to b}(x_b)m_{d\to b}(x_b)\\ \max_{a,b,c}p(a,b,c)=\max_{x_a}\psi_a(a)m_{b\to a}(x_a)\end{array} \]

我们依次对每个变量进行优化，实现起来将更加清晰明了。

相应地，它也具有数值优化版本——Max-Sum算法。此处不再赘述。

与因子形式的Sum-Product算法的联系

事实上，通过上述推导过程，我们发现仅有两类因子出现：\(\psi_{i,j}\)与\(\psi_i\)；相应地，我们可以反推出它的因子图具有这样的特点：每个因子节点都只与至多两个变量节点相连。

这是可以做到的。对于马尔可夫随机场来说，通过Hammesley-Clifford定理的证明，我们知道可以将势函数定义在任意的团结构上，而任意相互连接的两点都将构成合法的团结构。因此，我们通过在每条边上插入因子节点的手段来构造相应的因子图。除此之外，每个节点本身也是合法的团结构，所以我们可以自由地向每个节点额外连上一个因子节点。而对于贝叶斯网络来说，我们利用道德图将其转化为对应的马尔可夫随机场。

比如上面我们讨论的例子，对应的因子图为

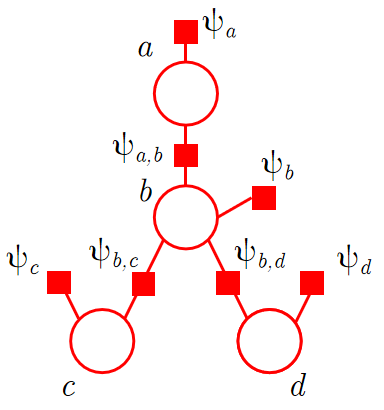
从这种意义上来说，非因子形式的Sum-Product算法可以看作是因子形式的Sum-Product算法的一个特例。由于没有充分利用因子图将节点进行“集中”的特性，非因子形式的Sum-Product算法将无法处理道德图“伦理”过程形成的环结构；但反过来，正因为它一次至多考虑两个节点，在利用衍生算法求最大后验时，将更易实现。

两种形式的Sum-Product算法各有特色，根据具体任务的需要与个人喜好进行挑选。