自动微分

计算图

概念：将计算流程表示为树结构；对于每一个运算，具有若干个输入\(x_1,\cdots,x_n\)和一个输出\(y=f(x_1,\cdots,x_n)\)

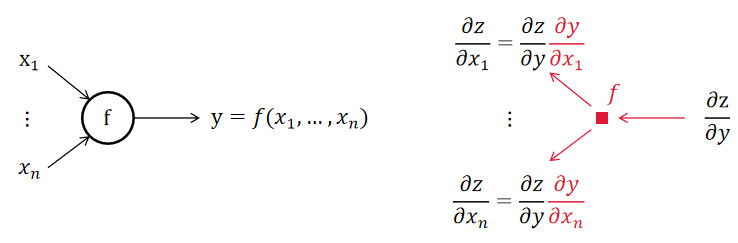
正向传播：由输入向输出方向进行计算

反向传播：利用链式法则\(\dfrac{\partial y}{\partial x}=\left(\left(\dfrac{\partial y}{\partial u_n}\dfrac{\partial u_n}{\partial u_{n-1}}\right)\cdots\right)\dfrac{\partial u_1}{\partial x}\)，从输出方向向输入方向累计梯度

• \(\dfrac{\partial y}{\partial x_i}=f(x_1,\cdots,x_n,y)\)，在正向传播时需记录并更新该节点处\(\dfrac{\partial y}{\partial x_i}\)的值

  反向传播需存储梯度是神经网络对显存要求高的根本原因

实现

框架：

class Layer:
    def __init__(self):
        self.x1, self.x2 = None
        self.y = None

    def forward(self, x1, x2):
        self.x1 = x1, self.x2 = x2
        self.y = f(x1, x2)
        return self.y

    def backward(self, dy):
        dx1 = dy * g(self.x1, self.x2, self.y)
        dx2 = dy * g(self.x1, self.x2, self.y)
        return dx1, dx2

\(\text{dx}:=\dfrac{\partial z}{\partial x}\)，由于被求导变量\(z\)在反向传播过程中保持不变，故利用自变量\(x\)标记偏导数 反向传播求得dx1, dx2后更新x1.grad, x2.grad = dx1, dx2

例：Sigmoid Layer \(y=\dfrac{1}{1+e^{-x}}\)

推导：\(\dfrac{\partial y}{\partial x}=\dfrac{e^{-x}}{(1+e^{-x})^2}=y(1-y)\)

图示：

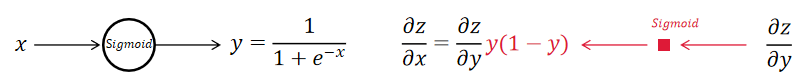
实现：

import numpy as np
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

class Sigmoid:
    def __init__(self):
        self.y = None

    def forward(self, x):
        self.y = sigmoid(x)
        return self.y

    def backward(self, dy):
        dx = dy * (1.0 - self.y) * self.y
        return dx

分离计算

背景：在反向传播过程中，若某些变量无需求偏导，则可不用记录其偏导数，将其从计算图中移除，从而节约存储空间