树
定义:A tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of
- A tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of
- and zero or more nonempty (sub)treesT1, ... , Tk, each of whose roots are connected by a directed edge from r
子树不能相连,故每个节点都是某些子树的根
\(N\)节点的树具有\(N-1\)条边
默认根绘制在最顶端
概念:
- 节点的度:节点的==子树个数==(与图的度不同)
- 树的度:\(\max\limits_{\text{node}\in\text{tree}}\set{\text{degree(node)}}\)
- 父亲:具有子树的节点
- 孩子:父亲节点子树的根
- 兄弟:同一个父亲的儿子
- 叶子:度为0的节点(无孩子)
- 路径:\(n_1\to n_k\)的唯一路径
- 路径长度:路径具有的边数
- 深度:根到该节点唯一路径的长度
- 高度:该节点到叶子节点最长路径的长度
深度,高度可以以顶点个数衡量(此时Depth(root) = 1),也可以以边数衡量(此时Depth(root) = 0),默认按边数衡量
- 树的高度:height(root) = depth(deepest leaf)
- 祖先:根到该节点路径上的所有节点
- 后代:子树中的全部节点
表示:
- 链表:( A ( B ( E ( K, L ), F ), C ( G ), D ( H ( M ), I, J ) ) )
-
左儿子右兄弟:
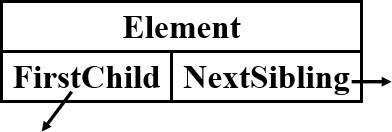
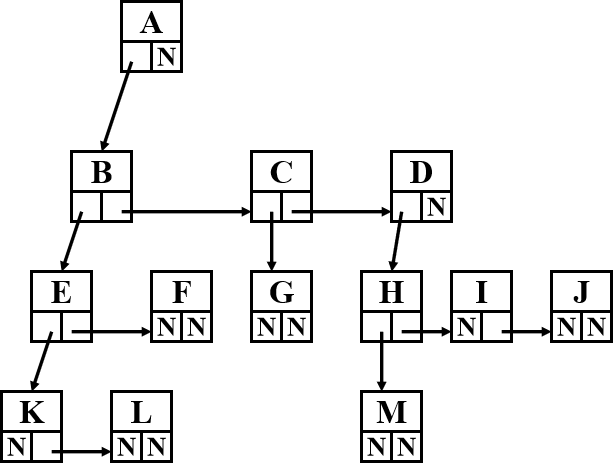
-
并查集:每个节点维护一个指向父亲的指针