栈

  • 概念：A stack is a Last-In-First-Out (LIFO) list, that is, an ordered list in which insertions and deletions are made at the top only.
  • 对象：A finite ordered list with zero or more elements.
  • 操作：
    1. IsEmpty
    2. CreateStack
    3. DisposeStack
    4. MakeEmpty
    5. Push
    6. Top
    7. Pop

实现：

  1. 链表：单向链表头做top

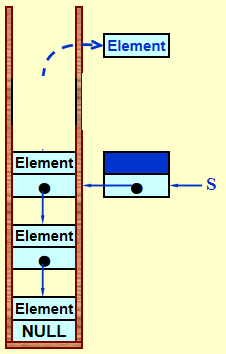
    image.png|200

    由于pop操作时需删除top，从而需要定位到新top，由于单向链表的单向性，故使top指向top下方的元素

    • Push：TmpCell->Next = S->Next, S->Next = TmpCell
    • Top：return S->Next->Element
    • Pop：FirstCell = S->Next, S->Next = S->Next->Next, free (FirstCell)

  2. 数组： 

      struct  StackRecord {
    int     Capacity ;              /* size of stack */
    int     TopOfStack;          /* the top pointer */
    /* ++ for push, -- for pop, -1 for empty stack */
    ElementType  *Array;    /* array for stack elements */
 } ;

应用：

  1. 括号匹配：将左括号入栈，碰到右括号时左括号出栈 
       Algorithm  {
    Make an empty stack S;
    while (read in a character c) {
        if (c is an opening symbol)
            Push(c, S);
        else if (c is a closing symbol) {
            if (S is empty)  { ERROR; exit; }
            else  {  /* stack is okay */
                if  (Top(S) doesn’t match c)  { ERROR, exit; }
                else  Pop(S);
            }  /* end else-stack is okay */
        }  /* end else-if-closing symbol */
    } /* end while-loop */ 
    if (S is not empty)  ERROR;
}

复杂度：\(T(N)=O(N)\)

  1. 表达式求值
  • 分类
    • 中缀表达式： a + b * c - d / e
    • 前缀表达式：- + a * b c / d e
    • 后缀表达式（逆波兰式）：a b c * + d e / -
  • 求值：
    • 后缀表达式求值：操作数入栈，碰到操作符时操作数出栈，计算后入栈
    • 前缀表达式转后缀表达式：操作符入栈，左括号入栈，碰到右括号时出栈至左括号出栈，碰到操作符时出栈至栈顶优先级低于自身，并入栈

  1. 系统调用栈

    image.png|300