图
定义:\(G(V,E)\)
- 无向图:\((v_i,v_j)=(v_j,v_i)\)
- 有向图:\(<v_i,v_j>\not=<v_j,v_i>\)
约定:
- 不研究重边、自环
完全图:a graph that has the maximum number of edges
邻接:
- 无向图:\(v_i,v_j\) are adjacent
- 有向图:\(v_i\) is adjacent to \(v_j\)
子图:\(G'\subset G\iff V(G')\subset V(G),E(G')\subset E(G)\)
路径:\(\set{v_p,v_{i1},\cdots,v_q}\quad s.t.(v_p,v_{i1}),\cdots,(v_{in},v_q)\)
路径长度:路径边数
简单路径:\(v_{i1},\cdots,v_{in}\)互不相同
环:路径上\(v_p=v_q\)
连接:存在\(v_i\to v_j\)的路径
连通:
- 强连通:任意两点都连通
- 强连通分量:最大强连通子图
- 弱连通:不考虑有向性时连通
树:连通的无环图(acyclic)
DAG:有向无环图
度:
- 无向图:连边数
- 有向图:出度、入度
定理:\(e=(\sum_{i=0}^{n-1}d_i)/2\)
表示:
- 邻接矩阵
性质:
- 无向图邻接矩阵对称
- 无向图:\(\text{degree}(i)=\sum_{j=0}^{n-1}\text{adj_mat[i][j]}\)
- 有向图:
- 出度:\(\text{degree}(i)=\sum_{j=0}^{n-1}\text{adj_mat[i][j]}\)
- 入度:\(\text{degree}(i)=\sum_{j=0}^{n-1}\text{adj_mat[j][i]}\)
问题:稀疏图浪费空间
- 邻接链表
graph[N],每条链连接顶点指向的出边
问题:无法找到指向该节点的顶点
解决:逆邻接表
-
合并邻接表、逆邻接表:十字链表
- 每个节点对应一条边
- 每个节点具有两个指针域,分别存邻接表指针、逆邻接表指针
-
多重链表
- 每个节点对应一条边
- 每个节点具有两个指针域,每个指针域指向自己的邻接表指针
拓扑排序¶
AOV网络:digraph G in which V( G ) represents activities and E( G ) represents precedence relations
前驱:i is a predecessor of j ::= there is a path from i to j
后继:i is an immediate predecessor of j ::= < i, j > \(\in\) E( G )
偏序关系:传递 + 反对称
DAG(directed acyclic graph):有向无环图
拓扑排序:A topological order is a linear ordering of the vertices of a graph such that, for any two vertices, i, j, if i is a predecessor of j in the network then i precedes j in the linear ordering
网络的拓扑排序不唯一
目标:Test an AOV for feasibility, and generate a topological order if possible
朴素算法:\(T=O(|V|^2)\)
void Topsort( Graph G )
{ int Counter;
Vertex V, W;
for ( Counter = 0; Counter < NumVertex; Counter ++ ) {
V = FindNewVertexOfDegreeZero( );
if ( V == NotAVertex ) {
Error ( “Graph has a cycle” ); break; }
TopNum[ V ] = Counter; /* or output V */
for ( each W adjacent to V )
Indegree[ W ] – – ;
}
}
图算法常见思路:根据当前点信息修改相连点的信息
BFS:用队列维护顶点集
void Topsort(Graph G) {
Queue Q;
int Counter = 0;
Q = CreateQueue(NumVertex);
MakeEmpty(Q);
for (each vertex V)
if (Indegree[V] == 0) Enqueue(V, Q);
while (!isEmpty(Q)) {
V = Dequeue(Q);
TopNum[V] = ++Counter;
for (each W adjacent to V)
if (--Indegree[W] == 0) Enquene(W, Q);
}
if (Counter != NumVertex) Error ("Graph has a cycle");
DisposeQueue(Q);
}
应用:有向图判环
最短路算法¶
路径长度:给定图\(G=(V, E)\), 边权\(c(e)\quad\forall e\in E(G)\),路径\(P\)长度为\(\sum\limits_{e_i\subset P}c(e_i)\)
最短路问题:给定带权图\(G=(V,E)\)和源点\(s\),找\(s\)到任何其它点的最短路径
存在负环时,最短路为\(-\infty\)
无权最短路:BFS
实现:
dist[]\(s\to v_i\)距离Known[]vis数组Path[]记录前驱形成路径 朴素算法:\(T=O(|V|^2)\)
BFS:\(T=O(|V|+|E|)\)
void Unweighted(Tabel T) {
Queue Q;
Vertex V, W;
Q = CreateQueue(NumVertex); MakeEmpty(Q);
Enqueue(S, Q);
while (!IsEmpty(Q)) {
V = Dequeue(Q);
T[V].Known = true;
for (each W adjacent to V) {
if (T[W].Dist == Infinity) { // 队列按搜索先后顺序放入元素,队头一定是最近的元素
T[W].Dist = T[V].Dist + 1;
T[W].Path = V;
Enqueue(W, Q);
}
}
}
DisposeQueue(Q);
}
带权最短路:Dijkstra
步骤:
- 划分已知点集,未知点集
- 从已知点集取具有最短路径的点V
- 找到与V相连的属于未知点集的点,松弛
每当一个点状态更新时,需同步更新相连点的状态
void Dijkstra(Table T) {
Vertex V, W;
for (;;) {
V = smallest unknown distance vertex;
if (V == NotAVertex) break;
T[V].Known = true;
for (each W adjacent to V)
if (!T[W].Known)
if (T[V].Dist + C[V][W] < T[W].Dist) {
Decrease(T[W].Dist to T[V].Dist + C[V][W]);
T[W].Path = V; // 记录用于更新的点
}
}
}
实现:
- 朴素实现 \(T=O(|V|^2+|E|)\)
- 建堆找最小值 \(T=O(|V|\log|V|+|E|\log|V|)=O(|E|\log|V|)\)
Dijkstra算法无法处理负环图
负权最短路:SPFA
- 可重复入队
void WeightedNegative(Table T) {
Queue Q;
Vertex V, W;
Q = CreateQueue(NumVertex); MakeEmpty(Q);
Enqueue(S, Q);
while (!IsEmpty(Q)) {
V = Dequeue(Q);
for (each W adjacent to V)
if (T[V].Dist + Cvw < T[W].Dist) {
T[W].Dist = T[V].Dist + Cvw;
T[W].Path = V;
if (W is not already in Q)
Enqueue(W, Q);
}
}
DisposeQueue(Q);
}
关键路径¶
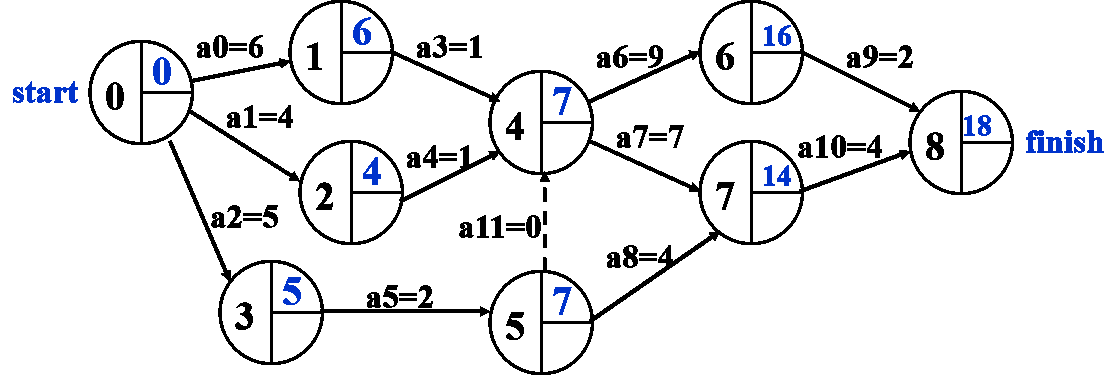
AOE网络:Activity On Edge Network, 顶点作为活动结束的信号
- EC Time:任务最早完成的时间
- LC Time:任务最晚需要被完成的时间
- 依赖关系使用边权为0的边表示
转移:
正向更新
反向更新
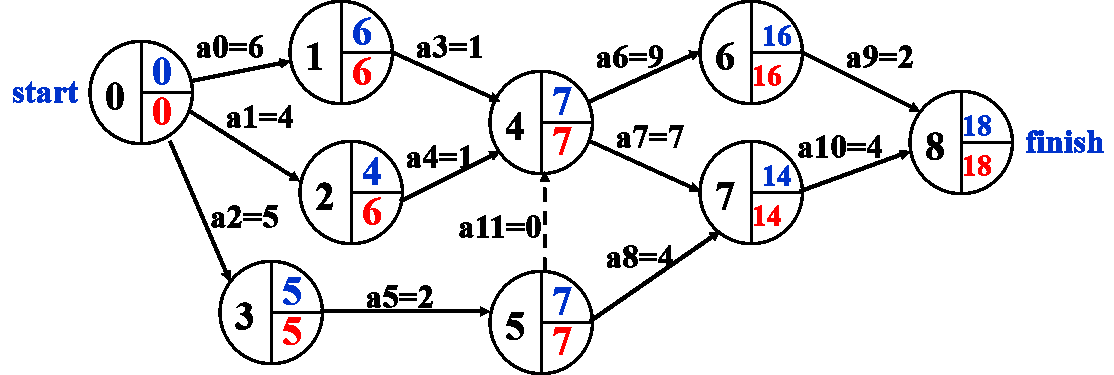
关键路径:EC == LC所有点形成的路径
全图最短路:Floyd(Dp) \(T=O(|V|^3)\)
- 状态:\(V_i\stackrel{S}\longrightarrow V_j\)
- 边界:\(V_i\stackrel{\emptyset}\longrightarrow V_j=\left\{\begin{array}{ll}\infty,&i\not\to j,\\w[i][j],&i\to j.\end{array}\right.\)
- 转移:\(V_i\stackrel{\set{1,\cdots,k+1}}\longrightarrow V_j=\min\set{V_i\stackrel{\set{1,\cdots,k}}\longrightarrow V_j,V_i\stackrel{\set{1,\cdots,k}}\longrightarrow V_{k+1}\stackrel{\set{1,\cdots,k}}\longrightarrow V_{j}}\)
网络流¶
概念:找源点\(s\)到汇点\(t\)的最大流量
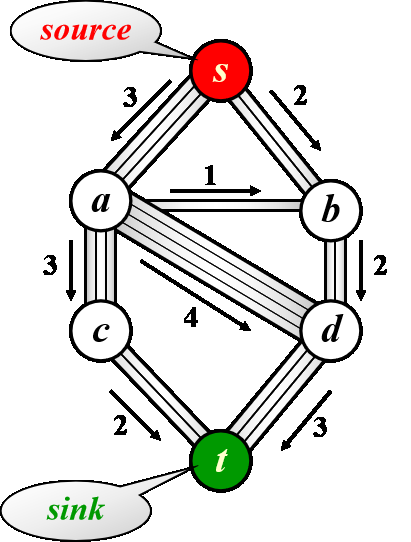
- 原图\(G\)
- 流量网络\(G_f\)
- 残差网路\(G_r\)
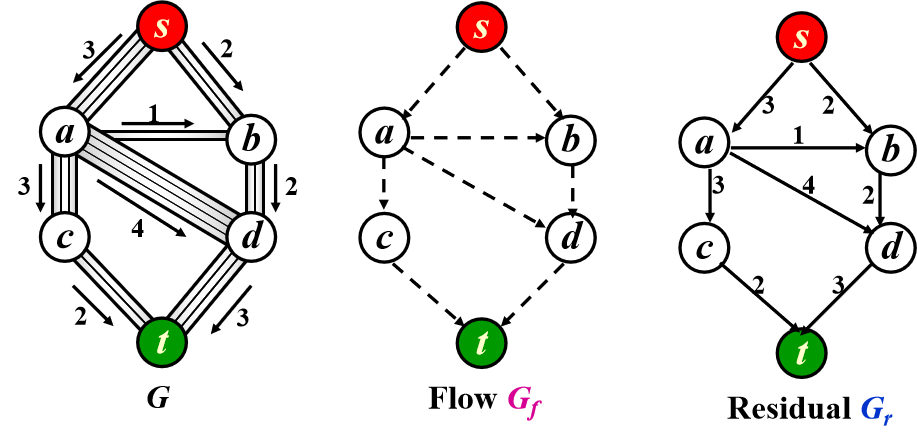
算法:
- 在\(G_r\)上找增广路\(s\to t\)
- 更新流量,残差
- 若\(G_r\)上仍存在增广路,回到1
复杂度:\(T=O(f\cdot|E|)\)
问题:特赦情况退化
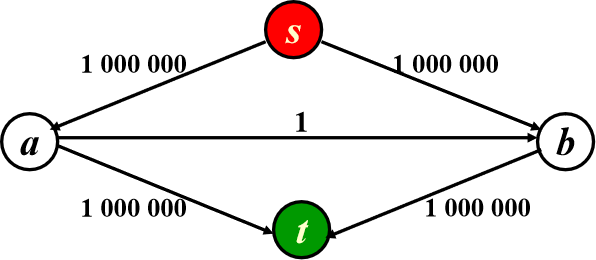
解决:
- 每次找最大增广路:\(T=T_{增广}*T_{找路}=O(|E|\log\text{cap}_\max)*O(|E|\log|V|)=O(|E|^2\log|V|)\)
- 每次找边最少增广路:\(T=O(|E|)*O(|E|\cdot|v|)=O(|E|^2|V|)\)
最小生成树¶
概念:A spanning tree of a graph G is a tree which consists of V( G ) and a subset of E( G )
思路:贪心
- 找最小边,找\(|V|-1\)条
- 边不能成环
Kruskal \(T=O(|E|\log|E|)\)
void Kruskal ( Graph G )
{ T = { } ;
while ( T contains less than |V|-1 edges
&& E is not empty ) {
choose a least cost edge (v, w) from E ;
delete (v, w) from E ;
if ( (v, w) does not create a cycle in T )
add (v, w) to T ;
else
discard (v, w) ;
}
if ( T contains fewer than |V|-1 edges )
Error ( “No spanning tree” ) ;
}
- 找最小边:堆
- 回路判断:并查集
Prim:始终找外部节点中距离最近的点加入生成树
Kruskal对边,Prim对点
BFS¶
void BFS() {
Queue Q;
Enqueue(S, Q);
while (!isEmpty(Q)) {
V = Dequeue(Q);
vis(V);
for (each W adjacent to V) {
Enqueue(W, Q);
}
}
}
DFS¶
访问所有点:
应用:连通分量计数双连通性¶
概念:
- 割点:移去割点后图连通性改变
- 双连通:不存在割点的图
- 双连通分量:最大双连通子图
求双连通分量:
- DFS生成树:利用DFS产生生成树,并打上DFS序
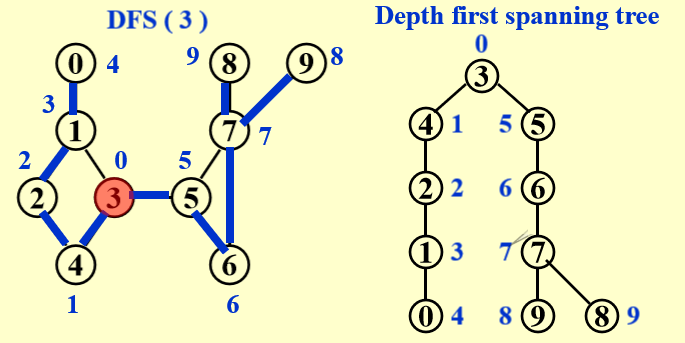
结论:所有不在DFS树上的边都是回边,即这些边都连接祖先与子孙,并不连接同级节点
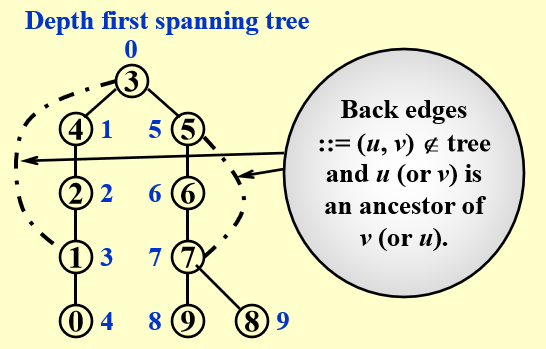
- 割点判据:
- 有两个儿子的根节点是割点
- 有子树的节点,子树通过非树边连接的最高点(DFS序更小的祖先)不超过该节点
刻画:low(u):该节点及其子树能连通的最高点(最小DFS序)
判据:
- \(u\)为根,且\(u\)至少有两个儿子
- \(u\)非根,\(\exists\) 1儿子 s.t. Low(child) \(\geqslant\) Num(u)
实现:
- DFS过程中打DFS序,更新Low
- 动态判断割点,并直接输出双连通分量
欧拉回路¶
定理:
- An Euler circuit is possible only if the graph is connected and each vertex has an even degree.
- An Euler tour is possible if there are exactly two vertices having odd degree. One must start at one of the odd-degree vertices.
算法:不断DFS,若走到重复点,则再开始一个DFS,直到所有边被访问