二叉树

定义：A binary tree is a [[树|tree]] in which no node can have more than two children

遍历：

  • 本质：二维结构序列化

    问题：遍历过程中未访问儿子的存储（访问某个儿子后失去对原父亲的索引）

    利用队列存储：BFS

    利用堆栈存储：DFS（函数调用栈）

  • 先序遍历：根左右 

    void preorder(tree_ptr tree) {
    if (tree) {
        visit(tree);
        for (each child C of tree) preorder(C);
    }
}

  • 后序遍历：左右根 
    void postorder(tree_ptr tree) {
    if (tree) {
        for (each child C of tree) postorder(C);
        visit(tree);
    }
}
  • 层次遍历：BFS 
    void levelorder(tree_ptr tree) {
    enqueue(tree);
    while (queue is not empty) {
        visit(T = dequeue());
        for (each child C of T) enqueue(C);
    }
}
  • 中序遍历：左根右 
    void inorder(tree_ptr tree) {
    if (tree) {
        inorder(tree->Left);
        visit(tree->Element);
        inorder(tree->Right);
    }
}

递归 \(\to\) 循环：

  • 尾递归可直接转为循环
  • 非尾递归利用栈可转循环

性质：前中后序遍历的堆栈操作完全相同（visit操作不影响堆栈操作）

推论：堆栈结构唯一确定树结构

循环实现中序遍历： 

void iter_inorder(tree_ptr tree) {
    Stack S = CreateStack(MAX_SIZE);
    for (;;) {
        for (;tree;tree = tree->Left) Push(tree, S); // 左边走到底
        tree = Top(S); Pop(S); // 作为根被访问
        if (!tree) break;
        visit(tree->Element);
        tree = tree->Right; // 向右走一步
    }
}
循环实现先序遍历： 
void iter_preorder(tree_ptr tree) {
    Stack S = CreateStack(MAX_SIZE);
    for (;;) {
        for (;tree;tree = tree->Left) {
            Push(tree, S);
            visit(tree->Element); // 作为左节点被访问
        }
        tree = Top(S); Pop(S);
        if (!tree) break;
        tree = tree->Right; // 向右走一步
    }
}
循环实现后序遍历：给作为左节点入栈和右节点入栈打上标记

表达式树的中缀遍历结果不一定是表达式的原始表达（需加括号）

线索二叉树：

  • 背景：N节点二叉树具有2N指针域，但仅有N-1条边，空间利用率低
  • 思想：让空指针域指向中序遍历的上/下一个节点
  • 实现：增加一个比特，用来标记是否为线索/儿子

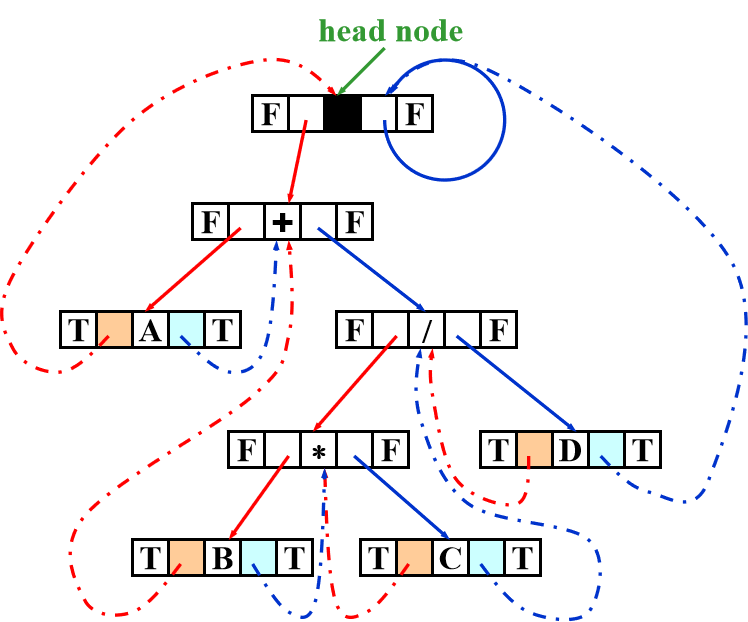
image.png|300

应用：树的遍历（增加一个特殊的head）

  • 向左走到低
  • 若为Thread，跳Thread
  • 否则向右走一步，然后向左走到底，重复两步直至终止

n个元素构成不同二叉树的个数：

  • In a binary tree, left child and right child are different.

  • 计数：\(C_n=\sum C_i\cdot C_{n-i-1}\)

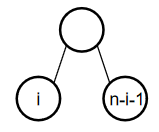
    image.png

  • 推广：n个元素构成的合法出栈序列

    二叉树确定，则遍历时的进出栈序列唯一确定；进出栈序列唯一确定，则二叉树确定，二者具有对应关系

分类：

  • 斜二叉树(Skewed Binary Trees)

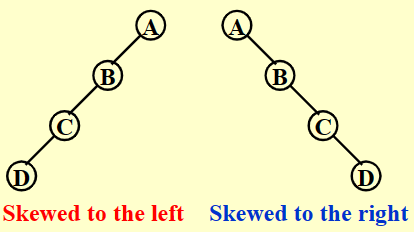
    image.png|300

  • 完全二叉树(Skewed Binary Trees)：All the leaf nodes are on two adjacent levels

性质：

  • 第i层节点数最多\(2^{i-1},i\geqslant1\)
  • \(k\)层深二叉树节点最多\(2^k-1,k\geqslant1\)
  • 结论：\(n_0=n_2+1\)
    • 推导：数边数：\(n_0+n_1+n_2-1=2*n_2+n_1\)