跳转至

排序

选择排序

步骤：每次选择最大的放最后

冒泡排序

步骤：若前一个元素大于后一个元素，交换；从第i个开始，共重复n轮

优化：记录上一次冒泡的终止位置，每次冒到终止位置即截止

插入排序

步骤：每次将没排好的元素插入 

void InsertionSort(ElementType A[], int n) {
    int j, P;
    ElementType Tmp;
    for (P = 1; P < N; P++) {
        Tmp = A[P];
        for (j = P; j > 0 && A[j-1] > Tmp; j--) A[j] = A[j - 1];
        A[j] = Tmp;
    }
}
\(T(N)=O(N^2)\)

普通排序算法的下界分析：

  • 逆序：\((i,j),i<j,A_i>A_j\)
  • 最好情况逆序数0，最坏情况（倒序）逆序数\(\dfrac{N(N-1)}{2}\)，平均逆序数\(\dfrac{N(N-1)}{4}\)

问题：不能在相邻位置比较，需要跳着比较和交换

希尔排序

思想：跳着比较

步骤：

  1. 分组：按组距分组，组内插入排序
  2. 减小组距再排序，直到组距为1

原理：

  • 插入排序在数据较有序时为\(O(n)\)，无序时为\(O(n^2)\)
  • 数据较乱时分组，\(O((n/k)^2\times k)=O(n^2/k)\)，优化复杂度
  • 后期数组较有序，为线性

分组策略：

  • 核心思想：防止数据落入同一组，导致重复比较
  • Hibbard's Increment Sequence：\(h_k=2^k-1\) \(O(N^{3/2})\)
  • Sedgewick's best sequence：\(h_k=9\times4^i–9\times2^i+1\) 
    void Shellsort(ElementType A[], int N) {
    int i, j, increment;
    ElementType Tmp;
    for (Increment = N / 2; Increment > 0; Increment /= 2) {
        // 插入排序
        for (i = Increment, i < N; i++) { // 抛去开头元素, 依次插入
            Tmp = A[i];
            for (j = i; j >= increment; j -= increment)
                if (Tmp < A[j - Increment]) A[j] = A[j - Increment];
                else break;
                A[j] = Tmp;
        }
    }
}

堆排序

思想：树形选择——次大点仅可能从叶子节点到根的路径上的点相遇过，比较次数降为\(\log\) 

BuildHeap(H); // O(N)
for (i = 0; i < N; i++)
    TmpH[i] = DeleteMin(H); // O(logN)
for (i = 0; i < N; i++)
    H[i] = TmpH[i];
\(T(N)=O(N\log N)\)

缺点：空间浪费

解决：删除\(\iff\)放在数组末尾，交换首尾元素后将根向下调整 

void HeapSort(ElementType A[], int N) {
    int i;
    for (i = N / 2; i >= 0; i--)
        PercDown(A, i, N); // BuildHeap: 从最后一个有儿子的节点开始向下调整
    for (i = N - 1; i > 0; i++) {
        Swap(&A[0], &A[i]); // DeleteMax
        PercDown(A, 0, i);
    }
}
\(T(N)=2O(N\log N)-O(N\log\log N)\)

问题：数组从0开始，堆从1开始，父子节点对应关系不同

归并排序

思想：分治

  1. 分：划分子问题
  2. 治：递归求解
  3. 合并

void MSort( ElementType A[ ], ElementType TmpArray[ ], 
        int Left, int Right ) 
{   int  Center; 
    if ( Left < Right ) {  /* if there are elements to be sorted */
    Center = ( Left + Right ) / 2; 
    MSort( A, TmpArray, Left, Center );     /* T( N / 2 ) */
    MSort( A, TmpArray, Center + 1, Right );    /* T( N / 2 ) */
    Merge( A, TmpArray, Left, Center + 1, Right );  /* O( N ) */
    } 
} 

void Mergesort( ElementType A[ ], int N ) 
{   ElementType  *TmpArray;  /* need O(N) extra space */
    TmpArray = malloc( N * sizeof( ElementType ) ); 
    if ( TmpArray != NULL ) { 
    MSort( A, TmpArray, 0, N - 1 ); 
    free( TmpArray ); 
    } 
    else  FatalError( "No space for tmp array!!!" ); 
}

/* Lpos = start of left half, Rpos = start of right half */ 
void Merge( ElementType A[ ], ElementType TmpArray[ ], 
           int Lpos, int Rpos, int RightEnd ) 
{   int  i, LeftEnd, NumElements, TmpPos; 
    LeftEnd = Rpos - 1; 
    TmpPos = Lpos; 
    NumElements = RightEnd - Lpos + 1; 
    while( Lpos <= LeftEnd && Rpos <= RightEnd ) /* main loop */ 
        if ( A[ Lpos ] <= A[ Rpos ] ) 
    TmpArray[ TmpPos++ ] = A[ Lpos++ ]; 
        else 
    TmpArray[ TmpPos++ ] = A[ Rpos++ ]; 
    while( Lpos <= LeftEnd ) /* Copy rest of first half */ 
        TmpArray[ TmpPos++ ] = A[ Lpos++ ]; 
    while( Rpos <= RightEnd ) /* Copy rest of second half */ 
        TmpArray[ TmpPos++ ] = A[ Rpos++ ]; 
    for( i = 0; i < NumElements; i++, RightEnd - - ) 
         /* Copy TmpArray back */ 
        A[ RightEnd ] = TmpArray[ RightEnd ]; 
}
\(T(N)=O(N+N\log N)\)

循环版本：两两合并

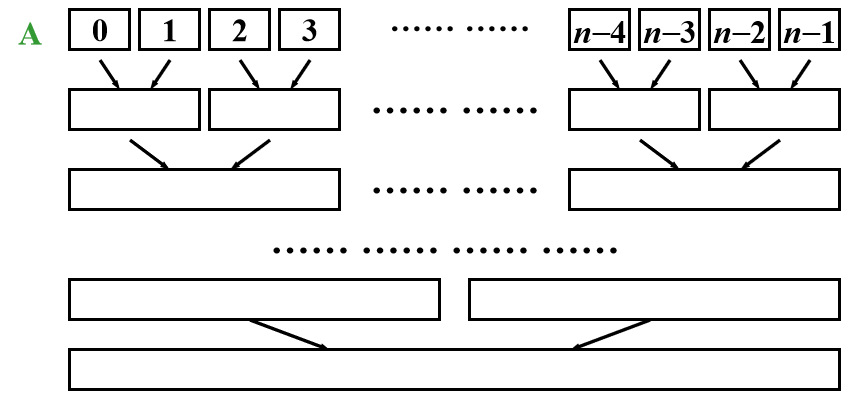
image.png|400

快速排序

void Quiclsort(ElementType A[], int N) {
    if (N < 2) return;
    pivot = pick any element in A[];
    Partition S = {A[] \ pivot} into two disjoint sets: 
        A1 = {a ∈ S | a <= pivot} and A2 = {a ∈ S | a >= pivot};
    A = Quicksort(A1, N1) ∪ {pivot} ∪ Quicksort(A2, N2);
}
关键步骤：划分

  • 思路：
    • 单边扫描：状态 小 | 大 [未知]，扫描时若大于主元则不操作，小于主元则与分界点交换
    • 双边扫描：状态 小 [未知] 大，扫描至小 | 大 [未知] 小 | 大时交换

循环设计思想：循环不变式 （处理过程中，什么关系一直存在）

相当于状态的确定：明确状态应是什么

例：快速排序划分——循环不变式：已处理序列应保持划分状态（小 | 大），状态由分界点确定；记录分界点位置，利用该点完成状态转移

主元确定：

  • 选A[0]：会被卡\(O(N^2)\)
  • 随机选取
  • 三选一：left, right, center找中间值 
    void Quicksort(ElementType A[],int N) {
    Qsort(A, 0, N - 1);
    /*A: the array */
    /*0: Left index */
    /*N-1: Right index */
}
/*Return median of Left, Center, and Right*/
/*Order these and hide the pivot*/
ElementTypeMedian3(ElementType A[], int Left, int Right) {
  int Center = (Left + Right) / 2;
  if (A[Left] > A[Center])
    Swap(&A[Left], &A[Center]);
  if (A[Left] > A[Right])
    Swap(&A[Left], &A[Right]);
  if (A[Center] > A[Right])
    Swap(&A[Center], &A[Right]);
  /*Invariant: A[Left] <= A[Center] <= A[Right] */
  Swap(&A[Center], &A[Right - 1]); /*Hide pivot*/
  /*only need to sort A[Left+1] ... A[Right-2]*/
  return A[Right - 1]; /*Return pivot */
}
void Qsort(ElementType A[], int Left, int Right) {
  int i, j;
  ElementType Pivot;
  if (Left + Cutoff <= Right) {      /*if the sequence is not to short */
    Pivot = Median3(A, Left, Right); /*select pivot */
    // 将最小元、最大元放在序列两端，保证循环不越界
    i = Left;
    j = Right - 1;
    for (;;) {
      while (A[++i] < Pivot);/*scan from left */ 
      while (A[--j] > Pivot);/*scan from right */
      if (i < j)
        Swap(&A[i], &A[j]); /*adjust partition */
      else
        break; /*partition done*/
    }
    Swap(&A[i], &A[Right - 1]); /*restore pivot */
    Qsort(A, Left, i - 1);      /*recursively sort left part */
    Qsort(A, i + 1, Right);     /*recursively sort right part */
  }                             /*end if - the sequence is long */
  else                          /*do an insertion sort on the short subarray*/
    InsertionSort(A + Left, Right - Left + 1);
}

时间复杂度：\(T(N)=T(i)+T(N-i-1)+cN\)，其中\(cN\)为划分时间；复杂度依赖于\(i\)

最坏：\(i=0\) \(T(N)=O(N^2)\)

最好：\(i=N/2\) \(T(N)=O(N\log N)\)

平均：

\[ T(N)=\dfrac{2}{N}\left[\sum_{j=0}^{N-1}T(j)\right]+cN\quad T(N)=O(N\log N) \]

应用：找序列第\(k\)大数

  • 划分： 小 | 主元 | 大
    • 判断\(k\)与 |大| 的关系，决定在哪个区间继续分治

表排序

问题：大结构排序时交换开销大，尽可能一次交换完成排序

解决：为每个元素打上下标

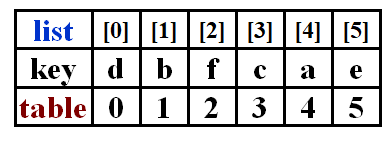
image.png|300

在table中指示排完后的元素的下标

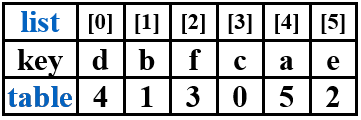
image.png|300

即list[table[0]],list[table[1]],...,list[table[n-1]]

然后对元素进行置换，置换过程形成一个环：先取首元素，再将所有元素均向前移，最后放入首元素

下界复杂度

定理：所有基于比较的排序算法最坏情况复杂度为\(\Omega(N\log N)\)

证明：决策树

  1. 比较过程构成决策树
  2. 决策树叶节点为所有可能排列，共\(N!\)个
  3. 故树高\(k\) s.t. \(N!\leqslant2^{k-1}\Rightarrow k\geqslant\log(N!)+1\)
  4. \(N!\geqslant (N/2)^{N/2}\Rightarrow\log(N!)\geqslant\Theta(N\log_2N)\)

桶排序

步骤：开一个桶，把数据丢进桶中，按序取出

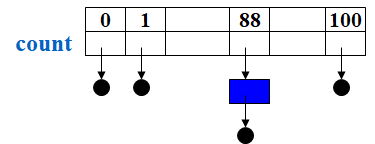
image.png|300

initialize count[ ]; 
while (read in a student’s record) 
    insert to list count[stdnt.grade]; 
for (i=0; i<M; i++) { 
    if (count[i]) 
    output list count[i];
}

基数排序

步骤：先将所有元素按最低位入桶，顺序取出后再按倒数第二位入桶，直至排序完毕

按照键\(K_i^j,K_i^0,K_i^{r-1}\)排序

MSD：最高位优先

LSD：最低位优先