哈希

问题：动态查找

思想：通过计算的方法查找元素

应用：字典问题

  • 符号表\(:=\set{<\text{name, attribute}>}\)
  • 用于比较字典中的字符串

ADT：A set of name-attribute pairs, where the names are unique

操作：

  • Sym Tab Create(TableSize)
  • Boolean Isln(symtab, name)
  • Attribute Find(symtab, name)
  • Sym TabInsert(symtab,name, attr)
  • Sym TabDelete(symtab,name)

概念：

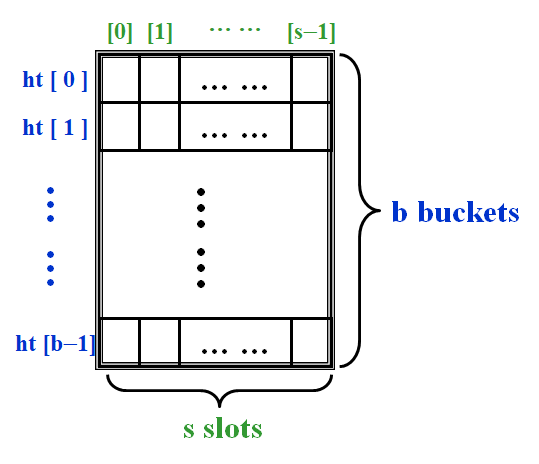
image.png|300

  • 哈希函数：f ( x ) = position of x in ht[ ] (i.e. the index of the bucket that contains x )
  • T := total number of distinct possible values for x
  • n := total number of identifiers in ht[ ]
  • identifier density := \(n/T\)
  • loading density \(\lambda\) := \(n/(sb)\)

问题：

  • 哈希碰撞：A collision occurs when we hash two nonidentical identifiers into the same bucket
    • 解决：设定哈希缓冲区
  • 溢出：An overflow occurs when we hash a new identifier into a full bucket.

当不存在溢出和碰撞时，\(T_{search}=T_{insert}=T_{delete}=O(1)\)

哈希函数设计：

  • 整数：
    • 求余法：\(f(x)=x\%m\) 其中\(m\)为素数
    • 平方取中：将\(x\)平方，取中间的位数（中间位数受各数字影响较大）
    • 折叠法：将数字分块，每部分按正反顺序排列后相加
    • 数字分析法
  • 字符串：
    • \(f(x)=(\sum x_i)\%\)TableSize 问题：利用率低
    • \(f(x)=(x_0+x_1\times27+x_2\times27^2)\%\)TableSize 问题：统计结果表明前三位组合少
    • \(f(x)=(\sum x_{N-i-1}\times32^i)\%\)TableSize
      • 使用32的幂可用位运算加速运算
      • 实现： 
        Index Hash3( const char *x, int TableSize )
{
    unsigned  int  HashVal = 0;
/* 1*/  while( *x != '\0' )
/* 2*/       HashVal = ( HashVal << 5 ) + *x++;
/* 3*/  return HashVal % TableSize;
}

        标准哈希函数：Probability\((f(x)=i)=1/b\)

链地址法：使用链表存储哈希值相同的元素 

struct  ListNode;
typedef  struct  ListNode  *Position;
struct  HashTbl;
typedef  struct  HashTbl  *HashTable;
struct  ListNode {
    ElementType  Element;
    Position  Next;
};
typedef  Position  List;
/* List *TheList will be an array of lists, allocated later */
/* The lists use headers (for simplicity), */
/* though this wastes space */
struct  HashTbl {
    int  TableSize;
    List  *TheLists;
};
初始化： 
HashTable  InitializeTable( int TableSize )
{   HashTable  H;
    int  i;
    if ( TableSize < MinTableSize ) {
        Error( "Table size too small" );  return NULL;  
    }
    H = malloc( sizeof( struct HashTbl ) );  /* Allocate table */
    if ( H == NULL )    FatalError( "Out of space!!!" );
    H->TableSize = NextPrime( TableSize );  /* Better be prime */
    H->TheLists = malloc( sizeof( List ) * H->TableSize );  /*Array of lists*/
    if ( H->TheLists == NULL )   FatalError( "Out of space!!!" );
    for( i = 0; i < H->TableSize; i++ ) {   /* Allocate list headers */
    H->TheLists[ i ] = malloc( sizeof( struct ListNode ) ); /* Slow! */
    if ( H->TheLists[ i ] == NULL )  FatalError( "Out of space!!!" );
    else    H->TheLists[ i ]->Next = NULL;
    }
    return  H;
}
查找： 
Position  Find ( ElementType Key, HashTable H )
{
    Position P;
    List L;
    L = H->TheLists[ Hash( Key, H->TableSize ) ];
    P = L->Next;
    while( P != NULL && P->Element != Key )  /* Probably need strcmp */
    P = P->Next;
    return P;
}
插入： 
void  Insert ( ElementType Key, HashTable H )
{
    Position   Pos, NewCell;
    List  L;
    Pos = Find( Key, H );
    if ( Pos == NULL ) {   /* Key is not found, then insert */
    NewCell = malloc( sizeof( struct ListNode ) );
    if ( NewCell == NULL )     FatalError( "Out of space!!!" );
    else {
         L = H->TheLists[ Hash( Key, H->TableSize ) ];
         NewCell->Next = L->Next;
         NewCell->Element = Key; /* Probably need strcpy! */
         L->Next = NewCell;
    }
  }
}

开放地址法： 

Algorithm: insert key into an array of hash table
{
    index = hash(key);
    initialize i = 0 ------ the counter of probing;
    while ( collision at index ) {
    index = ( hash(key) + f(i) ) % TableSize;
    if ( table is full )    break;
    else    i ++;
    }
    if ( table is full )
    ERROR (“No space left”);
    else
    insert key at index;
}
删除处理：打标记

平均成功查找次数：枚举，求平均（每个元素都去找一遍，求平均）

平均失败查找次数：

  • 分类计数：以哈希值为分类依据，查找次数——查找多少次能断定该元素不存在（例：若哈希函数为\(x\%M\)，讨论余数为\(0,\cdots,M-1\)每一类需要的次数）

线性探测：\(f(i)=i\)

问题：初始聚集，any key that hashes into the cluster will add to the cluster after several attempts to resolve the collision.

平方探测：\(f(i)=i^2\)

定理：若(1)哈希表元素一半不到 (2)表大小为素数，则任意插入都能找到空位

证明：只要证前\(\lfloor\)表大小/2\(\rfloor\) 次探测位置都不同，用反证法证明

实现：

查找： 

Position  Find ( ElementType Key, HashTable H )
{   Position  CurrentPos;
    int  CollisionNum;
    CollisionNum = 0;
    CurrentPos = Hash( Key, H->TableSize );
    while( H->TheCells[ CurrentPos ].Info != Empty &&
    H->TheCells[ CurrentPos ].Element != Key ) {
    CurrentPos += 2 * ++CollisionNum - 1; // (i+1)^2=i^2+(2i+1) 2i+1=2(i+1)-1
    if ( CurrentPos >= H->TableSize )  CurrentPos -= H->TableSize;
    }
    return CurrentPos;
}
插入： 
void  Insert ( ElementType Key, HashTable H )
{
    Position  Pos;
    Pos = Find( Key, H );
    if ( H->TheCells[ Pos ].Info != Legitimate ) { /* OK to insert here */
    H->TheCells[ Pos ].Info = Legitimate;
    H->TheCells[ Pos ].Element = Key; /* Probably need strcpy */
    }
}
变种：\(f(i)=\pm i\)

公共避冲区法：开一块空间专门处理冲突

双哈希法：\(f(i)=i+\text{hash}_2(x)\)

取法：\(\text{hash}_2(x)=R-x\%R\)

rehashing：将表扩大一倍，素数扩大一倍后找最近的素数

扩增条件：装载率超过一半