Morphology

研究对象：动物和植物结构

基础理论：集合论

一种简单的非线性代数算子

对象：主要用于二值图像，可扩展到灰度图像

应用：噪声过滤、形状简化、细化、分割、物体描述等（简化图像数据，保持它们基本的形状特性，并除去不相干的结构）

操作：

1. 膨胀
2. 腐蚀
3. 开操作
4. 闭操作 基本概念：

基本操作：

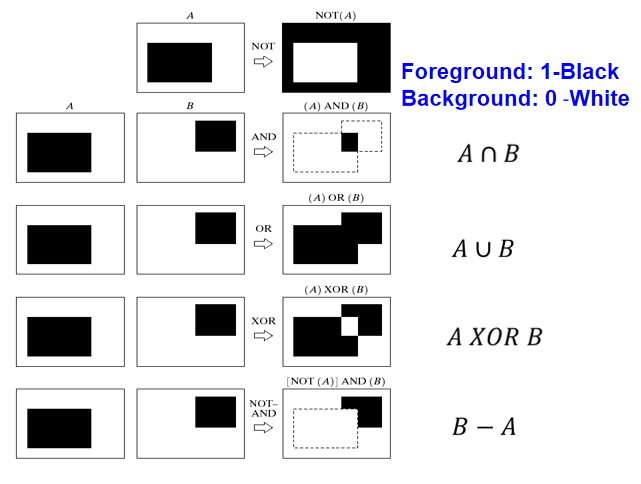
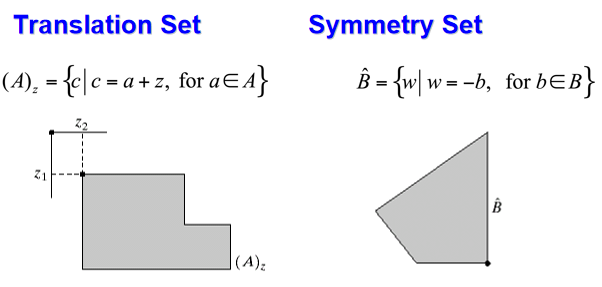
膨胀

输入：A 二值图像 B 结构元

定义：\(A\oplus B=\set{z|(B)_Z\cap A\not=\phi}\)

物理意义：膨胀是将与物体“接触”的所有背景点合并到该物体中，使边界向外部扩张的过程。可以用来填补物体中的空洞；其中“接触”的含义由结构元描述

例：

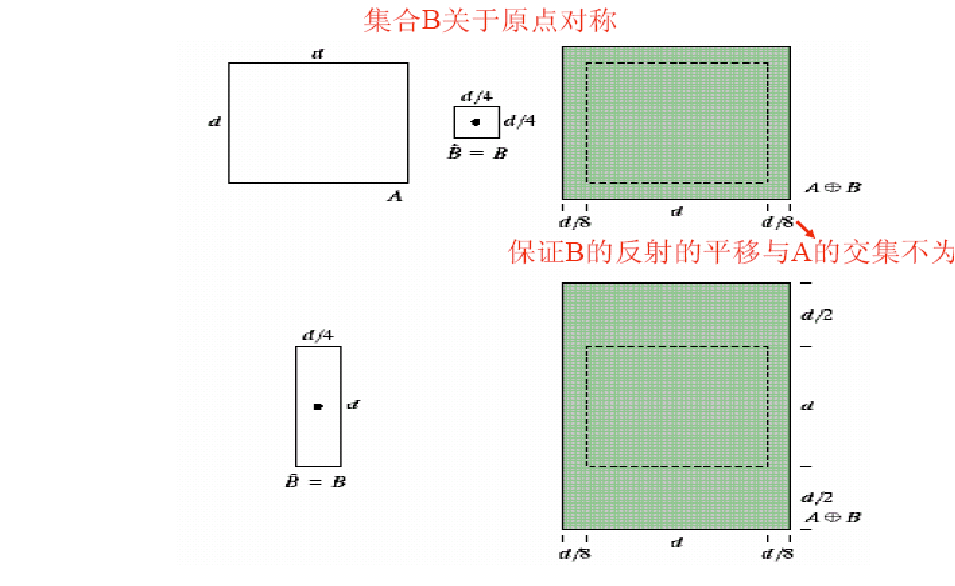
应用：缝隙填补

• 结构元：

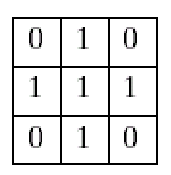
腐蚀

输入：A 二值图像 B 结构元

定义：\(A\ominus B=\set{(x,y)|(B)_{xy}\subset A}\) 物理意义：腐蚀是一种消除边界点，使边界向内部收缩的过程；可以用来消除小且无意义的物体

例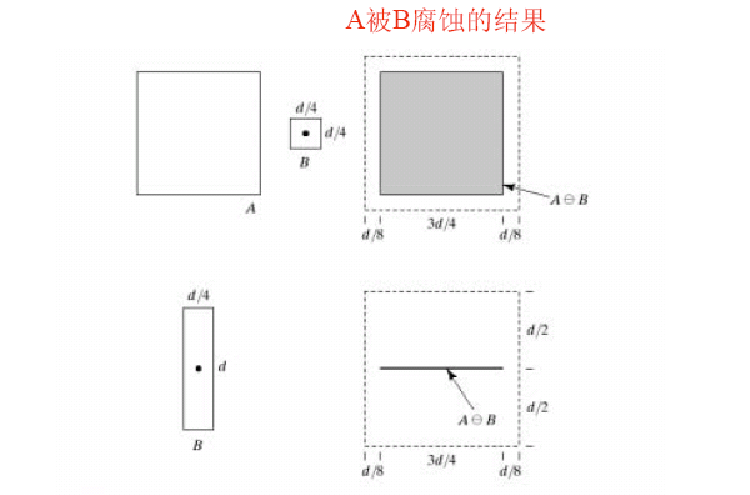： 应用：滤波

• 先腐蚀，后膨胀，滤去细节

膨胀与腐蚀的关系：对偶操作

• 定理：\((A\oplus B)^C=A^C\ominus B\)
• 证明：

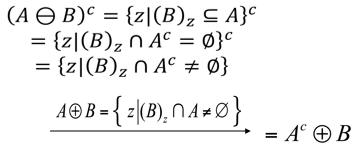
应用：

• 边缘提取：A - 腐蚀(A)
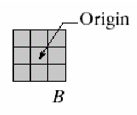
  • 结构元：
• 补洞：\(X_k=(X_{k-1}\oplus B)\cap A^C,k=1,2,\cdots\)迭代 初始条件\(X_0=p\)，终止条件\(X_k=X_{k-1}\)
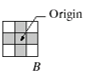
  • 结构元：
• 结构提取

开操作

定义：\(A\circ B=(A\ominus B)\oplus B\)

应用：消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积

闭操作

定义：\(A\bullet B=(A\oplus B)\ominus B\)

应用：用来填充物体内细小空洞、连接邻近物体、平滑其边界的同时并不明显改变其面积

对比：

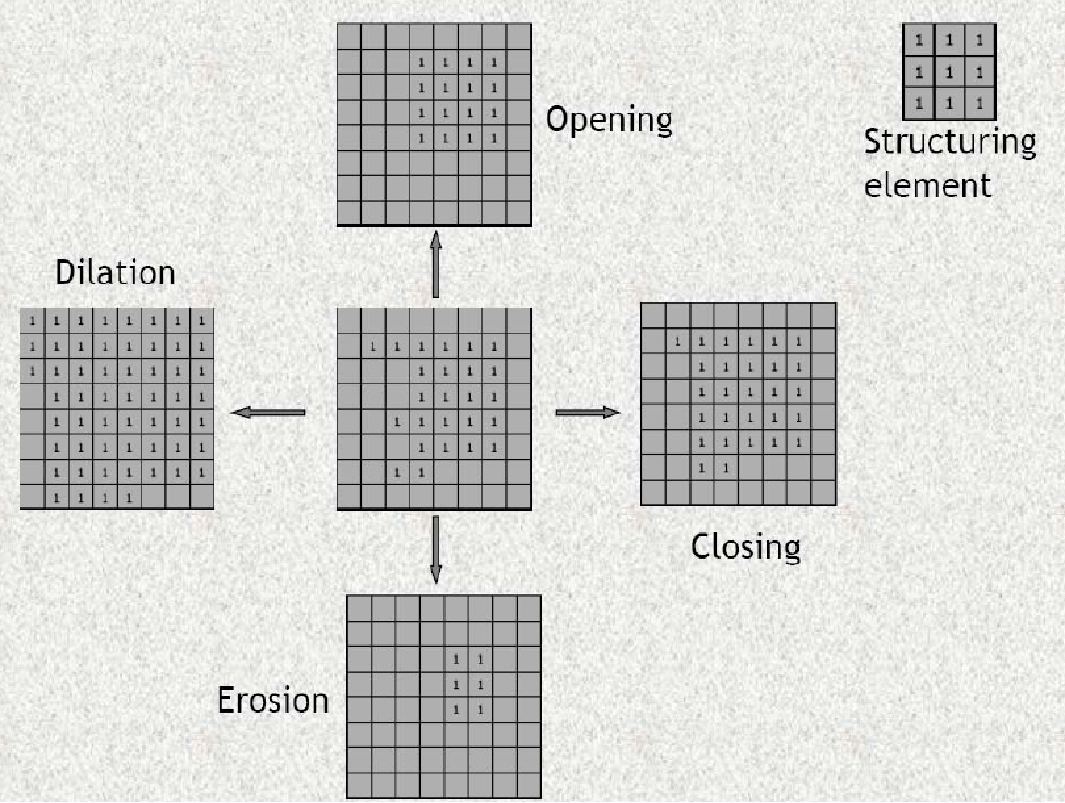
应用：指纹识别预处理