Interpolation

概念：插值是几何变换最常用的工具，利用已知像素值，采用不同的插值方法，可以模拟出未知像素的像素值

最近邻插值

概念：输出像素的灰度值等于离它所映射到的位置最近的输入像素的灰度值

步骤：

1. 计算该几何变换的逆变换，计算出P’所对应的原图像中的位置P
2. 寻找与P点最接近的像素Q，把Q点的像素值作为新图像中P’点的像素值 \((x',y')\to(x,y)\to(x_{\text{int}},y_{\text{int}})\to I_{\text{new}}(x',y')\to I_{\text{old}}(x_{\text{int}},y_{\text{int}})\)

问题：当图像中包含明显的几何结构时，结果将不太光滑连续，从而在图像中产生人为的痕迹（重复采样）

线性插值

一维：\(g_3=\dfrac{g_2-g_1}{x_2-x_1}(x_3-x_1)+g_1\)

二维（双线性插值）

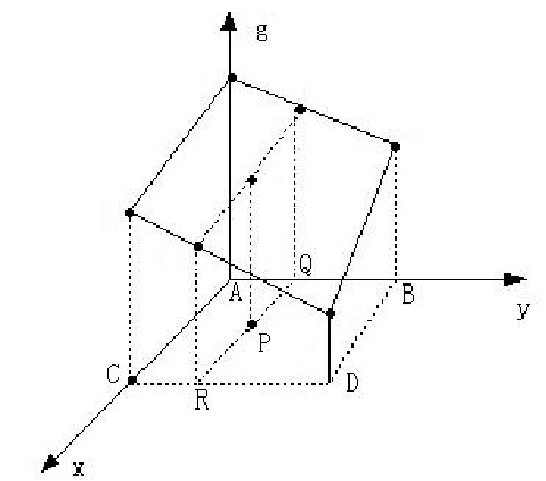
步骤：

1. 定义双线性方程\(g(x,y)=ax+by+cxy+d\)
2. 分别将A、B、C、D四点的位置和灰度代入方程，得到方程组
3. 解方程组，解出a、b、c、d四个系数
4. 将P点的位置代入方程，得到P点的灰度

径向基函数(RBF)插值

定义：\(G(x)=\sum_{i=1}^nw_iG(c_i),\quad w_i=\dfrac{\varphi(|x-c_i|)}{\sum_{i=1}^n\varphi(|x-c_i|)}\)

其中\(\mathbf x\)可以是标量或向量，可以是一维或多维插值；\(\varphi\)为核函数，\(c_{1..n}\)为控制点

核函数：\(\varphi(r)=\varphi(|x-x_i|)\)

• Gaussian：\(\varphi(r)=\exp(-\dfrac{r^2}{2\sigma^2})\)
• Multiquadrics：\(\varphi(r)=\sqrt{1+\dfrac{r^2}{\sigma^2}}\)
• Linear：\(\varphi(r)=r\)
• Cubic：\(\varphi(r)=r^3\)
• Thinplate：\(\varphi(r)=r^2\ln(r+1)\)