Image grayscale transform

可视化增强：对数操作

  • 目的：为了增强图像的可视信息，对图像中的像素进行基于对数的操作
  • 公式：\(L_d=\dfrac{\log(L_W+1)}{\log(L_\max+1)}\)，其中\(L_d\)是显示亮度，\(L_W\)是真实世界亮度，\(L_\max\)是场景最亮值
  • 性质：这个映射能够确保不管场景的动态范围是怎么样的，其最大值都能映射到1（白），其他的值能够比较平滑地变化
  • 原理：
    • Weber’s Law：\(\dfrac{\Delta I}{I}\approx K_{\text{weber}}\approx1\%\sim2\%\)
    • 假设连续两个灰度级之间的亮度差异是Weber’s Law中的可视临界值，则\(\dfrac{I_{\max}}{I_{\min}}=(1+K_{\text{weber}})^{255}\approx13\sim156\)
    • 传统显示对比度：
      • 阴极射线管 CRT: 100 : 1
      • 纸上打印：10：1
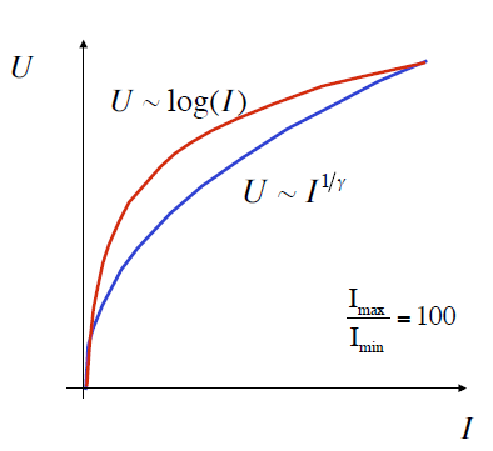
    • Fechner’s Law：人感知能力服从\(\log(I)\) （理想对数曲线）

\(\gamma\)矫正：

  • CRT显示器：
    • 通过调整电压可以调整亮度及其变化曲率，从而影响可视性和对细节的表现能力
    • \(U\sim I^{{1}/{\gamma}}\) image.png|250
  • 照相技术：
    • \(I\sim(\alpha\cdot I_0)^\gamma=a^\gamma\cdot{I_0}^\gamma\to\alpha\cdot{I_0}^\gamma\)
    • 与调整曝光时间效果近似相同
    • 应用：\(\gamma\)较大，提升视觉冲击力（用于设计）；\(\gamma\)较小，保留更多细节（用于机器学习）

灰度图像：

  • 概念：2D array composed by pixels (M rows×N columns), Each pixel is represented by 8 bits. The grayscales is divided into\(2^8\) = 256 levels, grayscale intensity p = 0,1,2,…,255

灰度直方图:

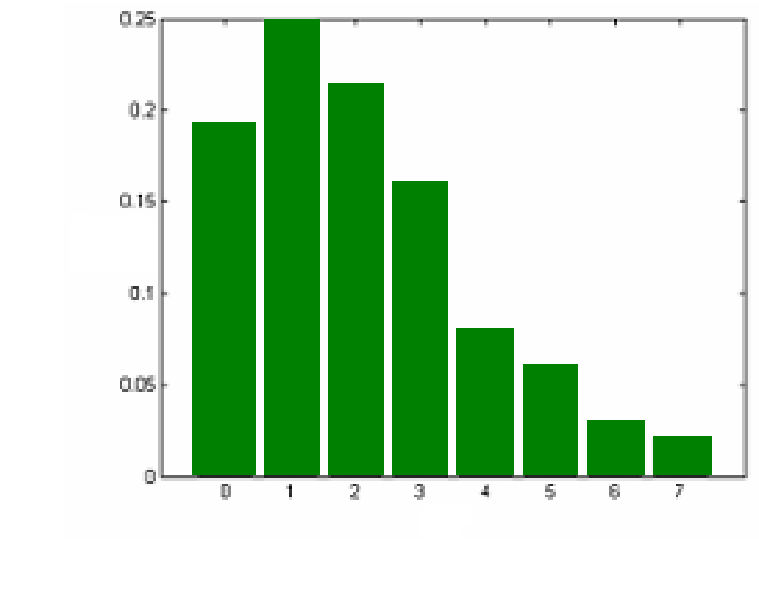
  • 概念：表示一幅图像中各个灰度等级的像素个数在像素总数中所占的比重 image.png|300
  • 函数关系：\(h(r_k)=n_k\qquad0\leqslant k\leqslant L-1,0\leqslant n_k\leqslant n-1\)
  • 概率密度函数：\(P(r_k)=n_k/n\quad\sum\limits_{k=0}^{L-1}P(r_k)=1\)

彩色直方图：

  • 概念：一幅图像中r,g,b通道上各个灰度等级的像素个数在像素总数中所占的比重
  • 应用：
    • 图像搜索：寻找直方图相近的图片
    • 拼图：将图像切割为小份，求每个小格子与待拼图直方图的欧式距离，选择相近的进行拼图（图像切的越小越能表现细节）
  • 问题：仅表现颜色分布，并不表示图像具体内容
  • 性质：
    • 空间域处理技术的基础
    • 反映图像灰度的分布规律，但不能体现图像中的细节变化情况
    • 对于一幅给定的图像，其直方图是唯一的
    • 不同的图像可以对应相同的直方图

直方图操作：

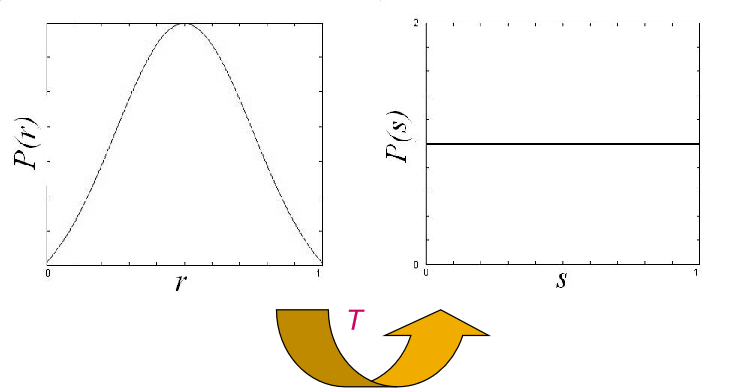
  • 直方图均衡化：将原图像的非均匀分布的直方图通过变换函数T修正为均匀分布的直方图，然后按均衡直方图修正原图像；图像均衡化处理后，图像的直方图是平直的，即各灰度级具有相同的出现频数 image.png|350
  • 操作：找到变换函数T，确定如下对应关系\(s=T(r)\)，从而确保输入图像中的每一个灰度r都能转换为新图像中的一个对应的灰度s
  • 算法：
    • 假设：
      1. 令r和s分别代表变化前后图像的灰度级，并且 0≤r,s ≤1
      2. P(r)和P(s) 分别为变化前后各级灰度的概率密度函数（r和s值已归一化，最大灰度值为1）
    • 规定：
      1. 在0≤r ≤1中，T(r)是单调递增函数，并且0≤T(r)≤1
      2. 反变换r = \(T^{-1}\)(s)也为单调递增函数
    • 推导： 灰度变换不影响像素的位置分布，也不会增减像素数目： \(\int_0^rP(r)\text dr=\int_0^sP(s)\text ds=\int_0^s1\cdot\text ds=s=T(r)\) 即\(s=T(r)=\int_0^rP(r)\text dr\)
    • 结论：转换函数T在变量r处的函数值s，是原直方图中灰度等级为[0,r]以内的直方图曲线所覆盖的面积
  • 推广：离散化
    • 设一幅图像的像素总数为n，分L个灰度级，nk为第k个灰度级出现的像素数，则第k个灰度级出现的概率为 \(P(r_k)=n_k/n\)
    • 离散化灰度直方图均衡化转换公式： $$ s_k=T(r_k)=\sum_{i=0}^kP(r_i)=\sum_{i=0}^k\dfrac{n_i}{n}=\dfrac{1}{n}\sum_{i=0}^kn_i $$

  • 例：

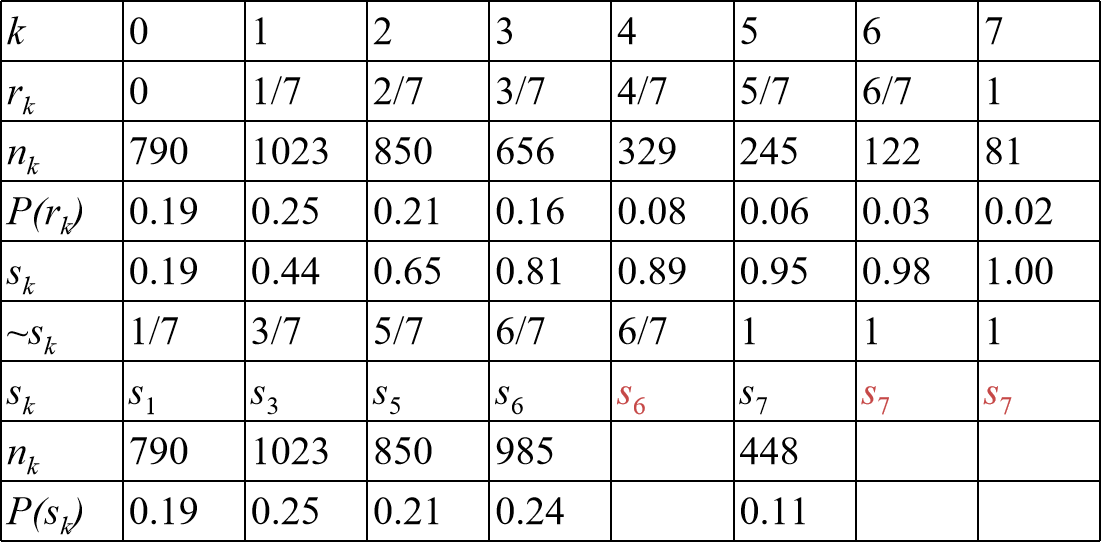
    image.png|400

  • 直方图匹配：修改一幅图像的直方图，使得它与另一幅图像的直方图匹配或具有一种预先规定的函数形状

    • 目标：突出我们感兴趣的灰度范围，使图像质量改善
    • 思路：利用直方图均衡化操作
    • 推导：\(r\mapsto z\)
      1. \(s=T(r)=\int_0^rP(r)\text dr\)
      2. \(v=T(z)=\int_0^zP(z)\text dz\)
      3. \(s,v\)分布相同，取\(v=s\)，求与\(r\)对应的\(z=G^{-1}(s)\)
    • 步骤：
      1. 计算获得两张表
      2. 选取一对\(v_k=s_j\)，查表得\(z_k,r_j\)
      3. \(r_j\mapsto z_k\)
  • 直方图变换：确定变换前后两个直方图灰度级之间对应关系的变换函数；经过直方图变换以后，原图像中的任何一个灰度值都唯一对应一个新的灰度值，从而构成一幅新图像
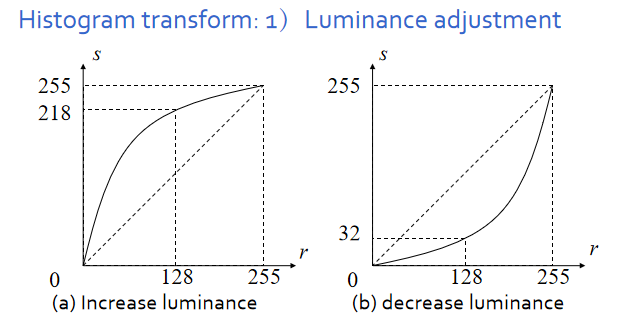
    • 亮度调整： image.png|350
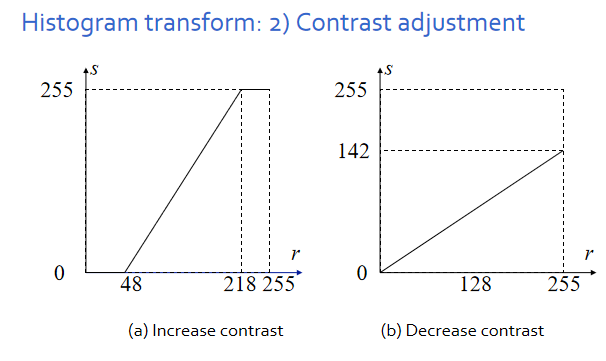
    • 对比度调整：(k = 1临界) image.png|350
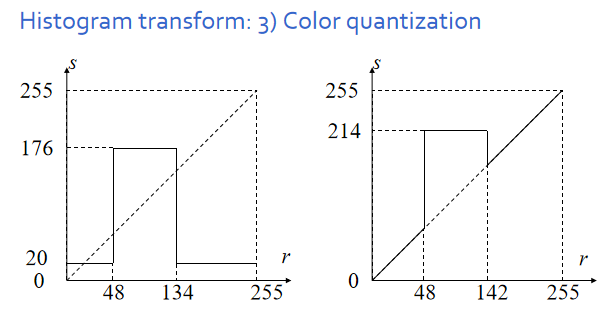
    • 颜色量化：将落在某区间的颜色设为固定值（离散化） image.png|350
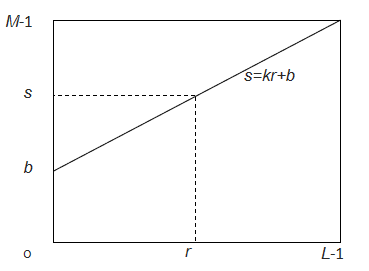
    • 线性变换：\(S=T(r)=kr+b\) image.png|200
      • 性质：
        • \(k>0\)变亮，\(k>1\)对比度变强（灰度散开），\(k<0\)颜色反转
        • 利用分段直方图变换，可以将感兴趣的灰度范围线性扩展，同时相对抑制不感兴趣的灰度区域
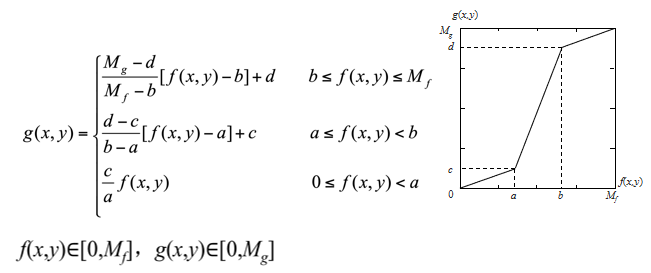
    • 分段线性变换： image.png|400
    • 非线性变换：
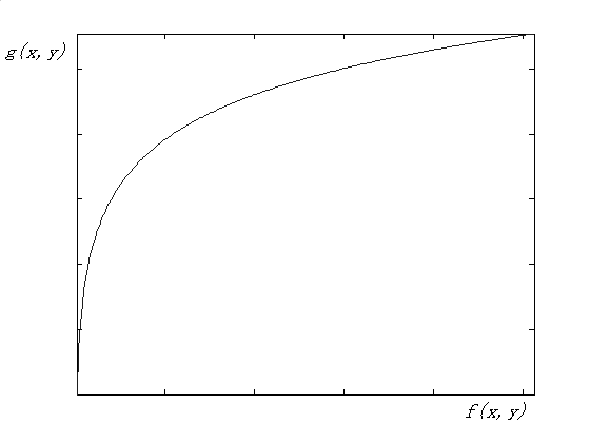
      • 对数变换：\(g(x,y)=a+\dfrac{\ln[f(x,y)+1]}{b\ln c}\) image.png|200
        • 拉升低灰度，压缩高灰度
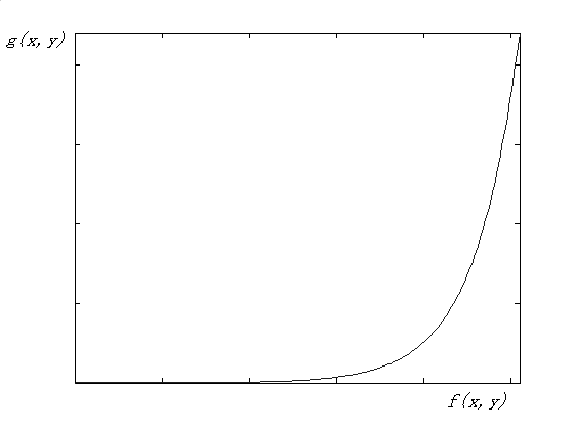
      • 指数变换：\(g(x,y)=b^{c[f(x,y)-a]}-1\) image.png|200
        • 拉升高灰度，压缩低灰度