Image feature

Invariant local features

不变量：translation, rotation, scale

特征检测：Harris corner detector

• 思想：角点更适合做特征点
• 刻画：找到包含大梯度且梯度朝向不同的窗口
• 推导：设窗口\(W\)位移为\((u,v)\)，SSD误差为

\[ E(u,v)=\sum_{(x,y)\in W}[I(x+u,y+v)-I(x,y)]^2 \]

\[I(x+u,y+v)\approx I(x,y)+\dfrac{\partial I}{\partial x}u+\dfrac{\partial I}{\partial y}v\approx I(x,y)+[I_x I_y]\begin{bmatrix}u\\ v\end{bmatrix}\]

\[E(u,v)\approx\sum_{(x,y)\in W}\left[[I_x I_y]\begin{bmatrix}u\\ v\end{bmatrix}\right]^2=\sum_{(x,y)\in W}[u\ \ v]\begin{bmatrix}I_x^2&I_xI_y\\ I_yI_x&I_y^2\end{bmatrix}\begin{bmatrix}u\\ v\end{bmatrix}\]

令\(H=\begin{bmatrix}I_x^2&I_xI_y\\ I_yI_x&I_y^2\end{bmatrix}\)，其两个特征向量方向为下降最快的方向

当\(\lambda_+,\lambda_-\)都大时为角点。

步骤：

1. 计算图像中每个点的梯度
2. 通过梯度得到每个windows的H矩阵
3. 计算特征值找到相应较大的点(\(\lambda_-\)>Threshold)
4. 选择那些\(\lambda_-\)是局部极大值的点作为特征

问题：计算量大

解决：Harris算子

\[ f=\dfrac{\lambda_1\lambda_2}{\lambda_1+\lambda_2}=\dfrac{\det(H)}{\text{tr}(H)} \]

性质：

• 旋转不变性
• 强度线性变换不变性：\(I\to I+b,I\to aI\)
• 无缩放不变性

解决：具有缩放不变性的特征检测

要求：在不同比例图像上极值点在同一个位置出现

Scale Invariant Detectors

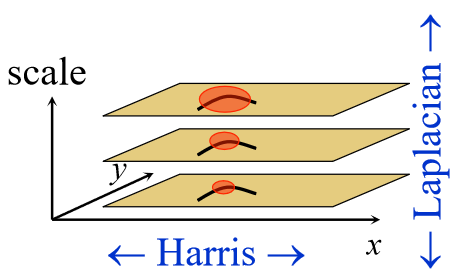
Harris-Laplacian

步骤：

1. 在不同尺度上做Harris角点检测
2. 若角点在不同尺度上都稳定存在，则通过第一道检验
3. 选择最优尺度：利用Laplace值，选择Laplace值最大的尺度

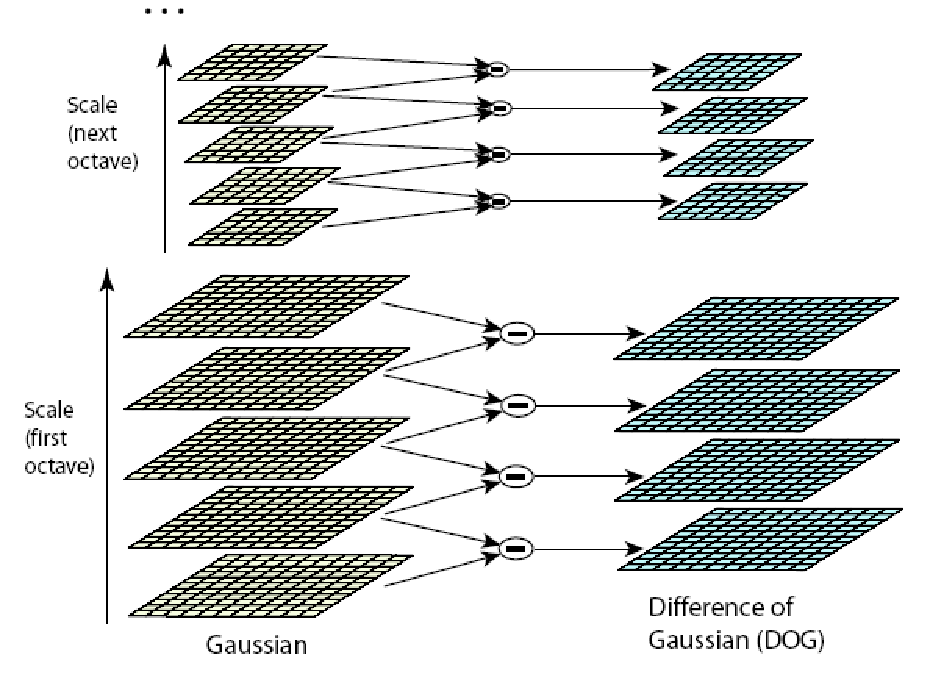
SIFT

卷积核：\(\text{DoG}=G(x,y,k\sigma)-G(x,y,\sigma)\)

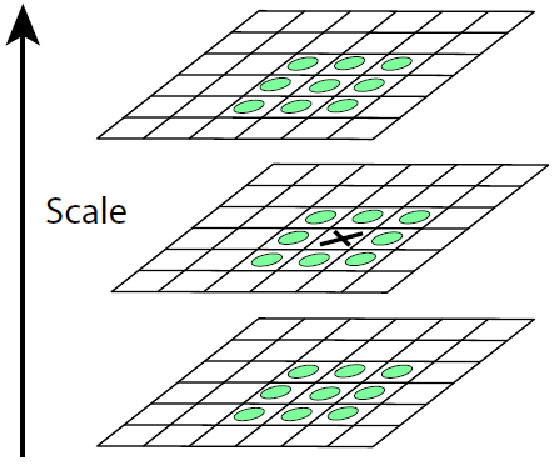
每个点同周围26个点比较来判断是否为极值

梯度/角度计算：

\[ m(x,y)=\sqrt{(L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2} \]

\[ \theta(x,y)=\sigma\tan 2((L(x,y+1)-L(x,y-1))/(L(x+1,y)-L(x-1,y))) \]

方向选择：

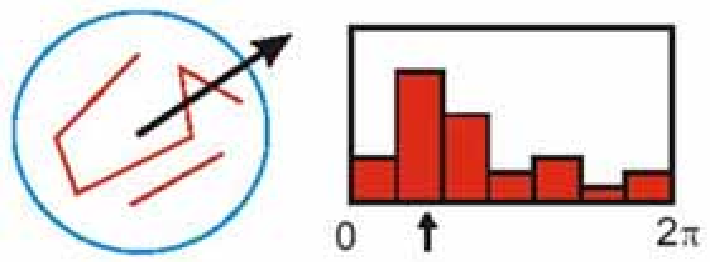
描述符：

• 不变性：在放射变换、亮度变换后不变的特征
• Scale Invariant Feature Transform：
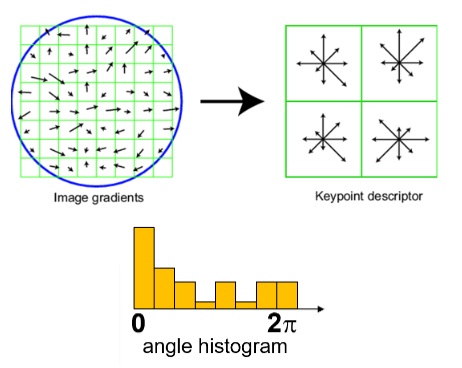
  • 步骤：
    1. 在检测到的特征角点周围选取16 * 16的方形窗口
    2. 计算每个像素的边的朝向（梯度的角度-90°）
    3. 剔除弱边缘（小于阈值梯度幅度）
    4. 创建剩下边的方向的直方图