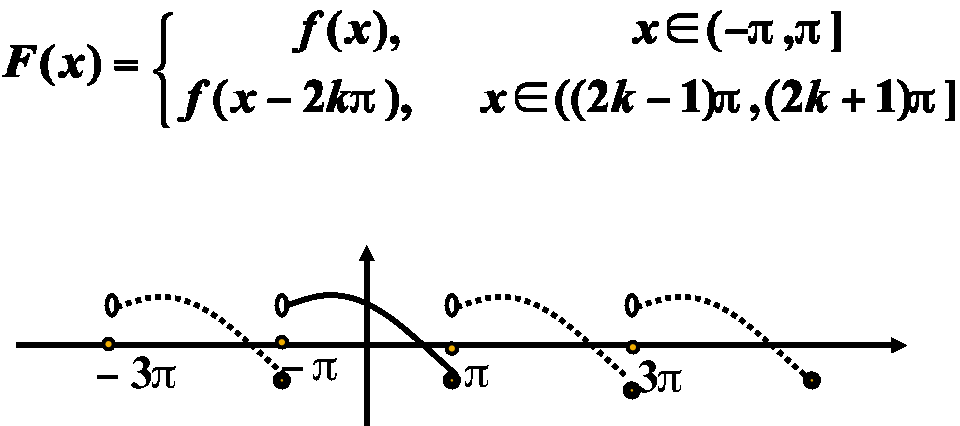Fourier Transform
Fourier级数:
\[
f(x)=\dfrac{1}{2}a_0+\sum_{n=1}^\infty a_n\cos(nx)+\sum_{n=1}^\infty b_n\sin(nx)
\]
\[
a_0=\dfrac{1}{\pi}\int_{-\pi}^\pi f(x)dx\quad a_n=\dfrac{1}{\pi}\int_{-\pi}^\pi f(x)\cos(nx)dx\quad b_n=\dfrac{1}{\pi}\int_{-\pi}^\pi f(x)\sin(nx)dx
\]
简谐振动:\(y=A\sin(\omega t+\varphi)\)
周期运动:
\[
y=\sum_{k=1}^ny_k=\sum_{k=1}^nA_k\sin(k\omega t+\varphi_k)
\]
周期延拓:对于非周期函数,如果函数\(𝑓(𝑥)\)只在区间\([−\pi,\pi]\)上,也可展开成傅氏级数
图像变换:

- Transform the image
- Carry out the task(s) in the transformed domain
- Apply inverse transform to return to the spatial domain
卷积核:
- 傅里叶变换 $$ T(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)r(x,y,u,v) $$
- 逆傅里叶变换 $$ f(x,y)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}T(u,v)s(x,y,u,v) $$
连续傅里叶变换:
- 傅里叶变换 $$ \mathcal F(f(x))=F(u)=\int_{-\infty}^\infty f(x)e^{-i2\pi ux}dx $$
- 逆傅里叶变换 $$ \mathcal F^{-1}(F(u))=f(x)=\int_{-\infty}^\infty F(u)e^{i2\pi ux}dx $$
频率与图像:
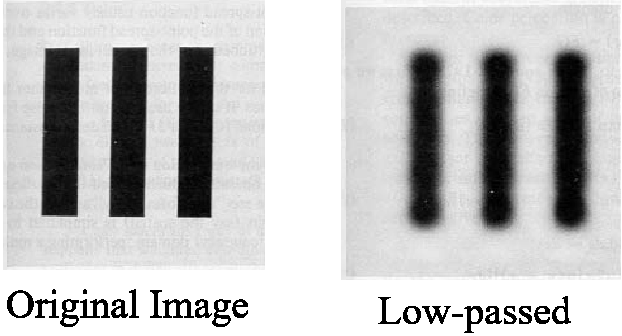
- Low frequencies correspond to slowly varying information (e.g., continuous surface)
- High frequencies correspond to quickly varying information (e.g., edges)
滤波步骤:
- 傅里叶变换\(\mathcal F(f(x))\)
- 去除不需要的频率\(D(\mathcal F(f(x)))\)
- 逆傅里叶变换\(f(x)=\mathcal F^{-1}(D(\mathcal F(f(x))))\)
离散傅里叶变换:
- 傅里叶变换: $$ F(u)=\sum_{x=0}^{N-1}f(x)e^{-\frac{i2\pi ux}{N}} $$
- 逆傅里叶变换: $$ f(x)=\dfrac{1}{N}\sum_{u=0}^{N-1}F(u)e^{\frac{i2\pi ux}{N}} $$
FFT:\(O(N^2)\to O(N\log n)\)
步骤:令\(W_N^{n,k}=e^{-i2\pi nk/N}\),则\(F(k)=\sum_{n=0}^{N-1}f(n)W_N^{n,k}\)
设\(N=2^H=2M\),则 $$ F(k)=\dfrac{1}{2M}\sum_{n=0}^{2M-1}f(n)W_{2M}^{n,k}=\dfrac{1}{2}\left[\dfrac{1}{M}\sum_{n=0}^{M-1}f(2n)W_{2M}^{2n,k}+\dfrac{1}{M}\sum_{n=0}^{M-1}f(2n+1)W_{2M}^{2n+1,k}\right] $$
又\(W_{2M}^{2n,k}=W_M^{n,k},W_{2M}^{2n+1,k}=W_M^{n,k}\cdot W_{2M}^{1,k}\),故
\[
F(k)=\sum_{n=0}^{M-1}f(2n)W_M^{n,k}+\sum_{n=0}^{M-1}f(2n+1)W_M^{n,k}W_{2M}^{k,1}
\]
令
\[\left\{
\begin{array}{l}
F_e(k)=\sum\limits_{n=0}^{M-1}f(2n)W_{M}^{n,k}\\
F_o(k)=\sum\limits_{n=0}^{M-1}f(2n+1)W_{M}^{n,k}
\end{array}
\right.
\]
故\(F(k)=F_e(k)+F_o(k)W_{2M}^{k,1}\)
递推即可。
二维FT:
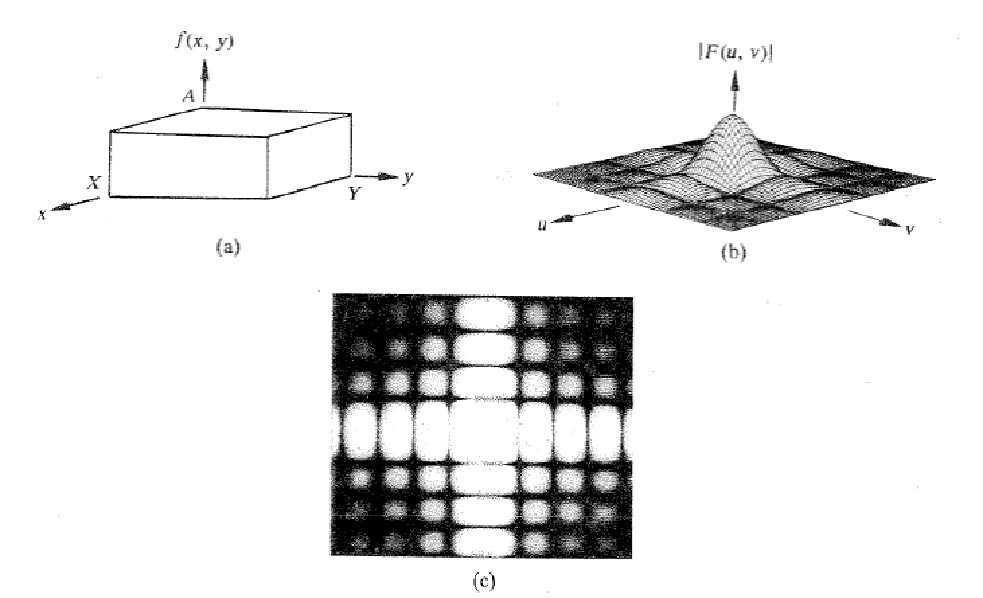
- 傅里叶变换: $$ \mathcal F(f(x,y))=F(u,v)=\int_{-\infty}^\infty f(x,y)e^{-i2\pi(ux+vy)}dxdy $$
- 逆傅里叶变换: $$ \mathcal F^{-1}(F(u,v))=f(x,y)=\int_{-\infty}^\infty\int_{-\infty}^\infty F(u,v)e^{i2\pi(ux+vy)}dudv $$
二维DFT:
- 傅里叶变换: $$ F(u,v)=\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}f(x,y)e^{-i2\pi(\frac{ux}{M}+\frac{vy}{N})} $$
- 逆傅里叶变换: $$ f(x,y)=\dfrac{1}{MN}\sum_{u=0}^{N-1}\sum_{v=0}^{N-1}F(u,v)e^{i2\pi(\frac{ux}{M}+\frac{vy}{N})} $$
图像的相位信息更重要