Convolution

连续一维卷积：

定义：\(g(x)=f(x)*h(x)=\int_{-\infty}^\infty f(t)h(x-t)\text{d}t\)，\(f(x)\)为输入，\(h(x)\)为卷积函数
性质：
- 交换率：\(f(x)*h(x)=h(x)*f(x)\)
- 分配律：\(f*(g+h)=f*g+f*h\)
- 结合律：\(f*(g*h)=(f*g)*h\)

离散一维卷积：\(g(x)=f(x)*h(x)=\dfrac{1}{M}\sum\limits_{t=0}^{M-1}f(t)h(x-t)\)

3x3卷积：

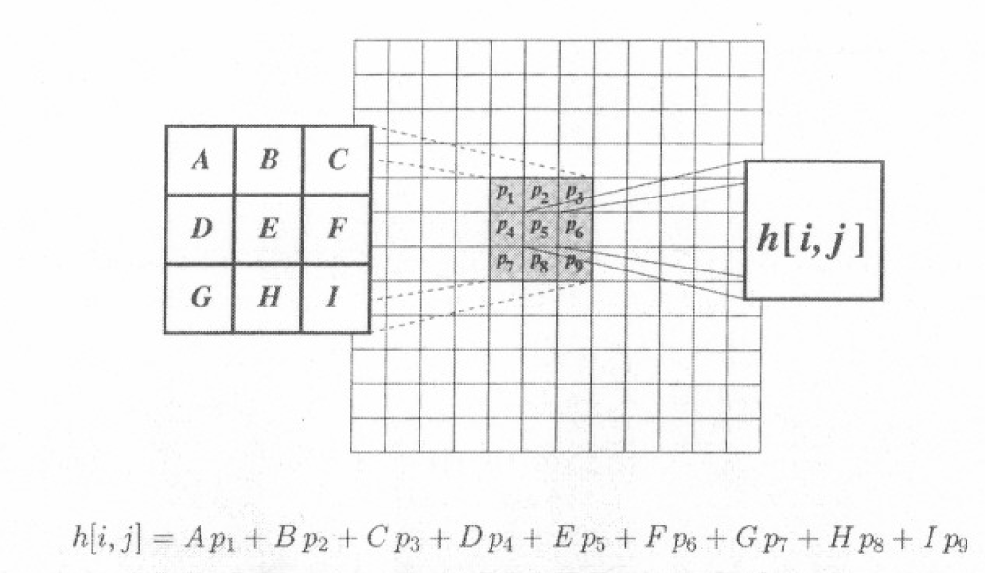
image.png|450

只更新中间的像素

Filtering¶

概念：滤波器是一个大小为M×N的窗口，窗口中的元素与原图像的处于窗口内的像素进行某种运算，结果作为新图像的一个像素。当窗口滑过原图像并完成上述运算之后，就能够得到一幅新图像

别名：滤波器、掩模、核、模板，窗口

滤波器子图像中的值是系数值，而不是像素值，它代表了影响新像素产生的权重

低通滤波：在待处理图像中逐点移动掩模，在每一点(x,y)处，滤波器在该点的响应通过实现定义的关系来计算。对于线性空间滤波，其响应由滤波器系数与滤波掩模扫过区域的对应像素值的乘积之和给出

通常，掩模的长宽都为奇数。假设分别为2a+1和2b+1。当窗口中心处于像素(x,y)处时，新的像素值为： \(g(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)\);对图像f中所有像素都与掩模进行运算之后，最终产生一幅新图像g
简化公式：\(R=w_1z_1+\cdots+w_{mn}z_{mn}=\sum_{i=1}^{mn}w_iz_i\)
目的：平滑处理
- 图像在传输过程中，由于传输信道、采样系统质量较差，或受各种干扰的影响，而造成图像毛糙，此时，就需对图像进行平滑处理。平滑可以抑制高频成分，但也使图像变得模糊
- 平滑空间滤波器用于模糊处理和减少噪声。模糊处理经常用于预处理，例如，在提取大的目标之前去除图像中一些琐碎的细节，桥接直线或曲线的缝隙

均值滤波：平滑线性空间滤波器的输出是包含在滤波掩模邻域内像素的简单平均值

\[ g(x,y)=\dfrac{\sum\limits_{s=-a}^a\sum\limits_{t=-b}^bw(s,t)f(x+s,y+t)}{\sum\limits_{s=-a}^a\sum\limits_{t=-b}^bw(s,t)} \]

其中，滤波器大小为(2a+1) ×(2b+1)，w为滤波器，f为输入图像，g为输出图像.

滤波掩模的大小与图像的平滑效果有直接的关系。当掩模比较小时，可以观察到在整幅图像中有轻微的模糊，当掩模大小增加，模糊程度也随之增加

应用：为了对感兴趣物体得到一个粗略的描述而模糊一幅图像，这样，那些较小物体的强度与背景混合在一起了，较大物体变得像“斑点”而易于检测。掩模的大小由那些即将融入背景中去的物件尺寸来决定

中值滤波：统计滤波器是一种非线性的空间滤波器，它的响应是基于窗口内图像区域中像素值的排序，由统计排序结果决定的值代替中心像素的值；统计滤波器中最常见的例子就是中值滤波器

性质：
- 用像素邻域内灰度的中值代替该像素的值
- 提供了优秀的去噪能力，比小尺寸的线性平滑滤波器的模糊程度明显要低
- 对处理脉冲噪声（也称为椒盐噪声）非常有效，因为这种噪声是以黑白点叠加在图像上的
操作：
1. 求中值\(\xi\)
2. 将掩模内欲求的像素及其邻域的像素值排序，确定出中值，并将中值赋予该像素点
应用：
- 去除那些相对于其邻域像素更亮或更暗，并且其区域小于\(n^2/2\)（滤波器区域的一半）的孤立像素集
- 突出图像中的细节或者增强被模糊了的细节

图像锐化：微分算子

微分算子是实现锐化的工具，其响应程度与图像在该点处的突变程度有关。微分算子增强了边缘和其他突变（如噪声）并削弱了灰度变化缓慢的区域
微分转差分：\(\dfrac{\partial f}{\partial x}=f(x+1)-f(x)\quad\dfrac{\partial^2f}{\partial x^2}=f(x+1)+f(x-1)-2f(x)\)
分类：
- 梯度算子
  - \(\nabla f=[G_x^2+G_y^2]^{\frac{1}{2}}=\left[(\dfrac{\partial f}{\partial x})^2+(\dfrac{\partial f}{\partial y})^2\right]^{\frac{1}{2}}\)
  - 简化计算：\(\nabla f\approx|G_x|+|G_y|\)
  - 推广：Robert 交叉梯度算子 \(\nabla f\approx|z_9-z_5|+|z_8-z_6|\)
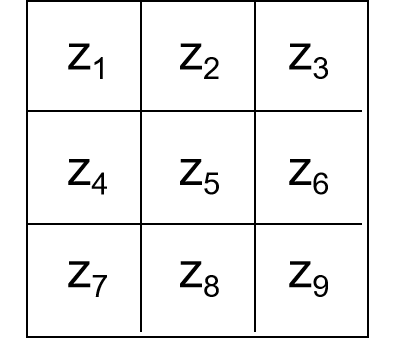
- Laplacian算子：\(\nabla^2f=\dfrac{\partial^2f}{\partial x^2}+\dfrac{\partial^2f}{\partial y^2}\)
  - 离散形式：\(\nabla^2f=[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)\)
  - 矩阵形式：
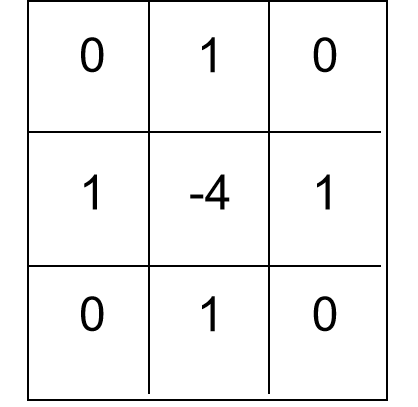
  - 推广：对角线上的元素也可以考虑进来设计掩膜
    - \(\nabla^2f=\sum_{i=-1}^1\sum_{j=-1}^1f(x+i,y+j)-9f(x,y)\)
  - 操作：将原始图像和拉普拉斯图像叠加在一起的简单方法可以保护拉普拉斯锐化处理的效果，同时又能复原背景信息
    - \(g(x,y)=\left\{\begin{array}{ll}f(x,y)-\nabla^2f(x,y)\\ f(x,y)+\nabla^2f(x,y)\end{array}\right.\)
      
      当拉普拉斯滤波后的图像与其它图像合并时（相加或相减），则必须考虑符号上的差别

问题：高斯滤波无法增强，锐化滤波无法去噪

解决：双边滤波——同时滤波&去噪

双边滤波：