Storage Elements and Sequential Circuit Analysis

Introduction to Sequential Circuits

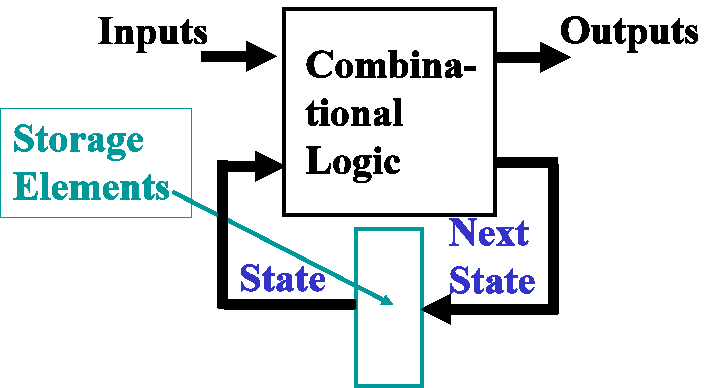
次态方程：\(\text{Next State}=f(\text{Input},\text{State})\)

输出方程：

• Mealy：\(\text{Outputs}=g(\text{Inputs},\text{State})\)
• Moore：\(\text{Outputs}=h(\text{State})\)

分类：

• 同步系统：
  • Behavior defined from knowledge of its signals at discrete instances of time（周期性同步更新）
  • Storage elements observe inputs and can change state only in relation to a timing signal (clock pulses from a clock)
• 异步系统：
  • Behavior defined from knowledge of inputs an any instant of time and the order in continuous time in which inputs change（非同步更新）
  • If clock just regarded as another input, all circuits are asynchronous

Latch

Basic (NAND) \(\bar S\)-\(\bar R\) Latch

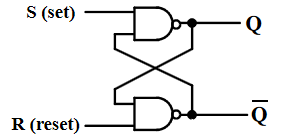
• R = 1, S = 1：此时假设Q = 0 / 1都是稳态，即保持历史状态；若历史状态unknown，为x
• R = 1, S = 0：将Q置位为1
• R = 1, S = 1：Q保持1
• R = 0, S = 1：将Q复位为0
• R = 1, S = 1：Q保持0
• R = 0, S = 0：将Q, \(\bar Q\)置1（禁止）
• R = 1, S = 1：最后状态为一个1，一个0，由NAND门传输门延迟决定，延迟低的为1（不确定值）

Basic (NOR) S-R Latch

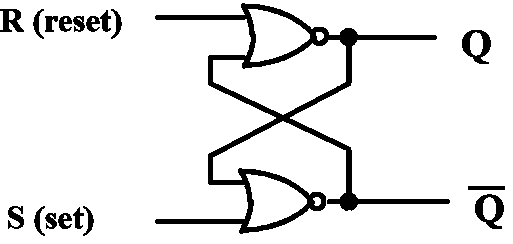
Clocked S-R Latch

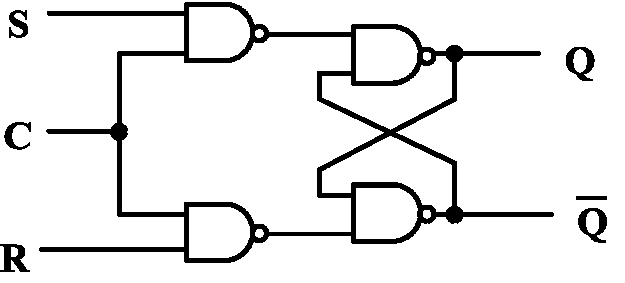
• C = 0：hold
• C = 1：\(\bar S-\bar R\)锁存器

D Latch

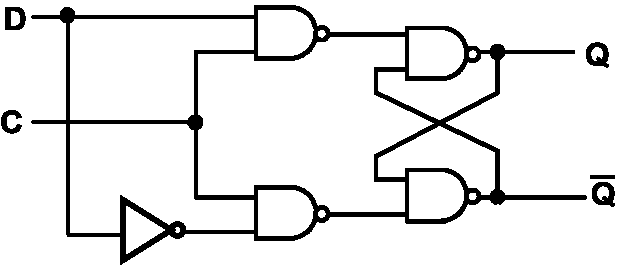
• C = 0：hold
• C = 1：禁止输入相同的操作，D = 1 / 0 为set / reset（Q = D）

  计算门延迟时不算\(G_n\)而算\(G\)：触发器给出输出\(Q,\bar Q\)

问题：构造触发器Flip-Flops(#1 Q = ~Q;)时

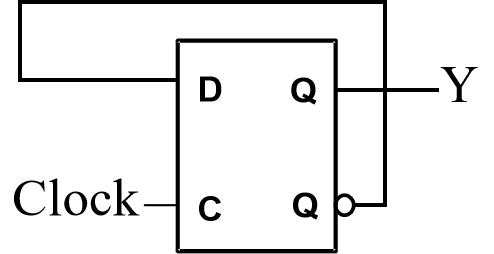
若置Clock = 1，则输出开始震荡，产生空翻现象

本质：D直接改变输出Q

期望：每个周期改且仅改一次（不让输入直接改变输出）

解决：

• S-R主从触发器
• 边沿触发器

触发器：信号更新不再依赖于输入改变，而是依赖于触发信号（输入不再直接改变输出）

S-R Master-Slave Flip-Flop

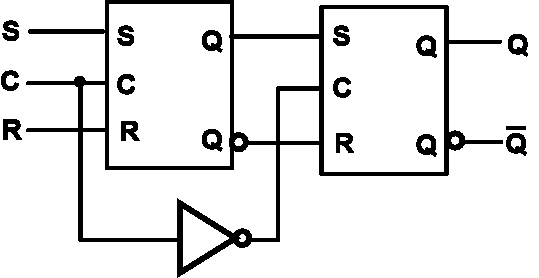
性质：

• 每个周期接收且仅接受一次外部输入
• 脉冲触发：上升沿主锁存器接收信号，一个脉冲结束后，下降沿更新从锁存器

问题：一次性采样

• 当S = 0, R = 0，C处于上升沿时，此时为保持状态；若S抖动，则S\(\uparrow\downarrow\)时Q'被置并保持（S上跳的恢复操作为R上跳，并非S恢复），在下降沿到来时将状态传递到Q导致主触发器状态被破坏

解决：边沿D触发器

Edge-Triggered D Flip-Flop

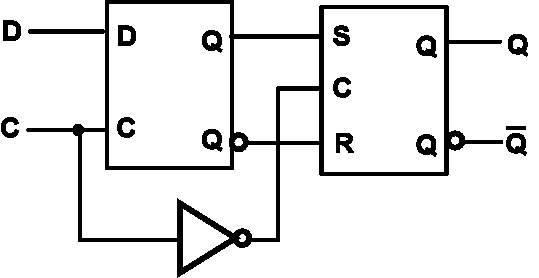
C = 1时，D\(\uparrow\downarrow\)互为逆操作，Q与D同步跳动（D上跳的恢复操作即D恢复）；下降沿时D的结果即为最后结果

Positive-Edge Triggered D Flip-Flop

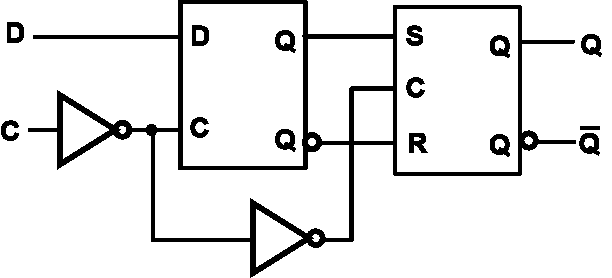
上升沿到来时，采集D输入；下降沿到来后更新Q状态

标准触发器

电路符号：

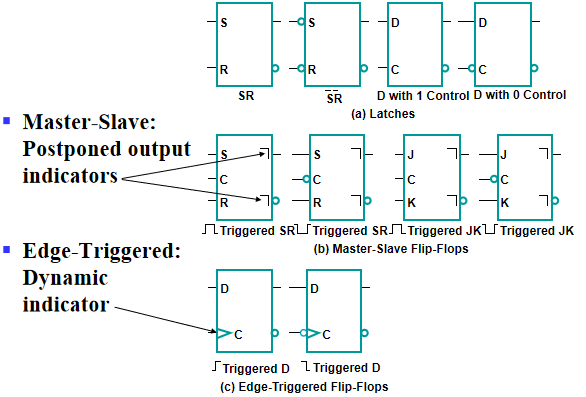
初值设定：

• 异步赋初值：通过S, R直接改变触发器的值

  

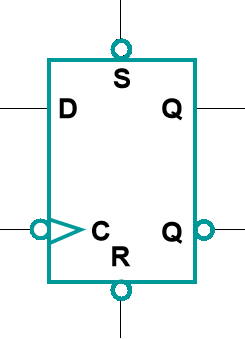
• 同步赋初值：通过改变D输入的值改变触发器的值

Sequential Circuit Analysis

模型：

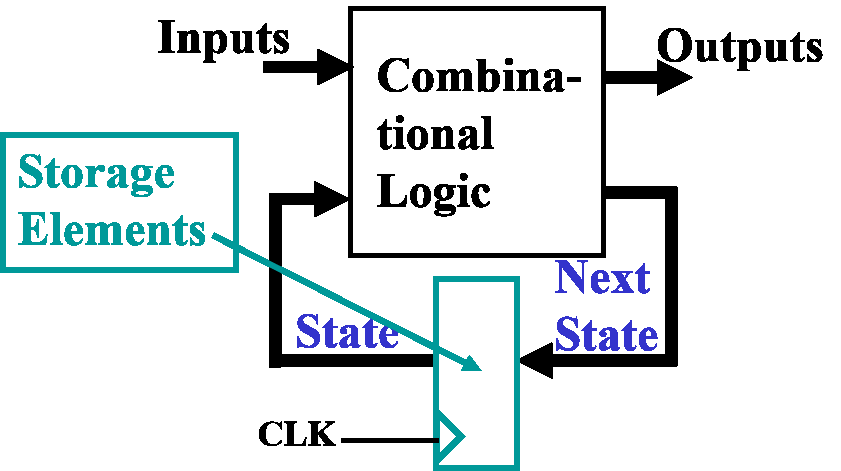
• 现态：在当前时刻t存储在触发器中的状态
• 次态：t+1时刻的状态，is a Boolean function of State and Inputs
• 输出

  时钟信号不是输入信号，是系统组成的一部分

例：

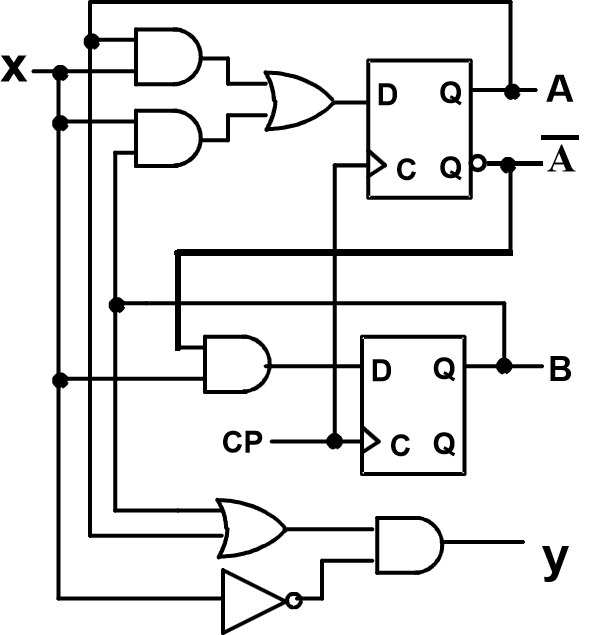
• 输入：\(x(t)\)
• 输出：\(y(t)\)
• 状态：\((A(t),B(t))\)

  认为触发器的输出是电路的状态，n个触发器具有\(2^n\)个状态

• 时钟脉冲：\(CP\)
• 输出函数与次态方程：
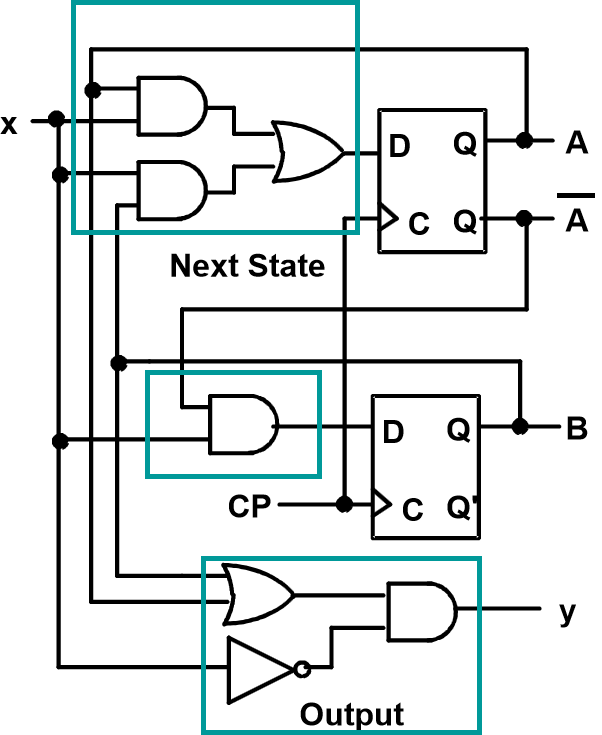
  • \(D_A\)：由触发器前的组合电路决定，\(D_A(t)=A(t)x(t)+B(t)x(t)\)
  • \(D_B(t)=\bar A(t)x(t)\)
  • 次态方程：由于D触发器激励方程为\(Q(t+1)=D(t)\)，故
    • \(A(t+1)=A(t)x(t)+B(t)x(t),B(t+1)=\bar A(t)x(t)\)
  • 输出方程：\(y(t)=\bar x(t)(B(t)+A(t))\)

    t时刻为上升沿到来的时刻（clk=1开始更新）

状态表：a multiple variable table with the following four sections

• Present State – the values of the state variables for each allowed state
• Input – the input combinations allowed
• Next-state – the value of the state at time (t+1) based on the present state and the input
• Output – the value of the output as a function of the present state and (sometimes) the input

  类似真值表，枚举\(A(t),B(t),x(t)\)得到\(A(t+1),B(t+1)\)与\(y(t)\)

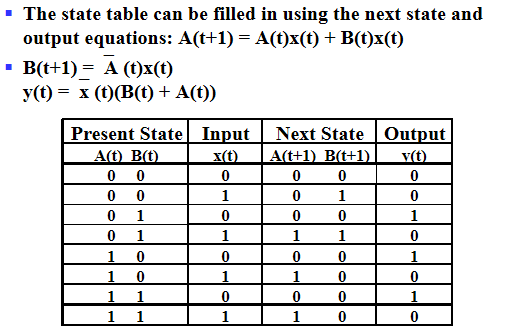
问题：状态转移难以观察

解决：Alternate State Table

• A(t), B(t)类似卡诺图排列（非严格），2-dimensional table that matches well to a K-map. Present state rows and input columns in Gray code order

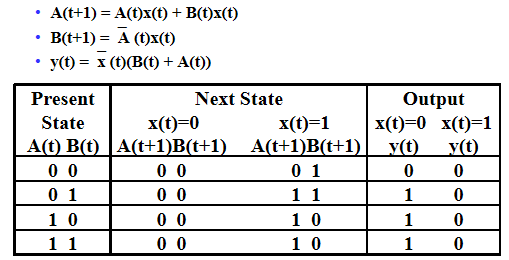
问题：不直观

解决：状态图

• A circle with the state name in it for each state
• A directed arc from the Present State to the Next State for each state transition
• A label on each directed arc with the Input values which causes the state transition, and
  • On each circle with the output value produced, or
  • On each directed arc with the output value produced

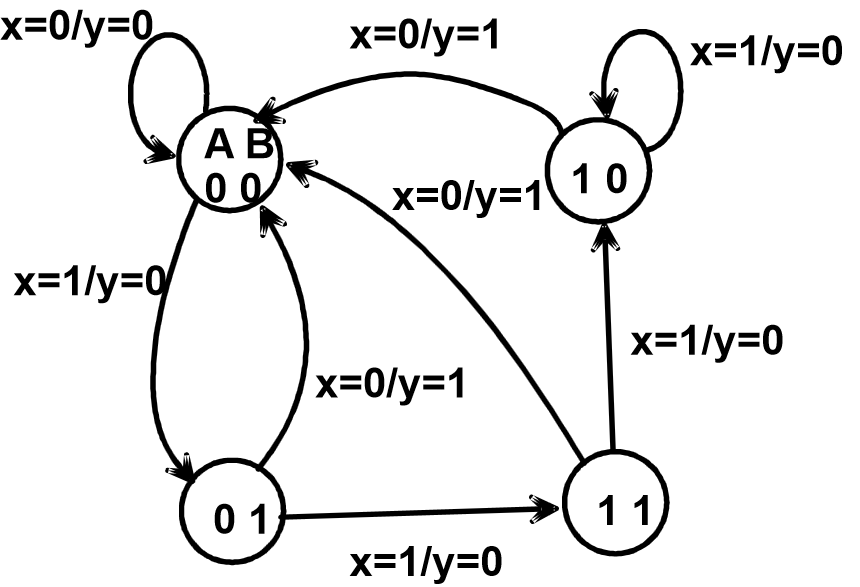
等效状态：从两个状态出发，给定相同的输出序列，若次态和输出都一致，则说明两个状态等效，可合并 + 目的：减少状态以减少触发器的数量

例：

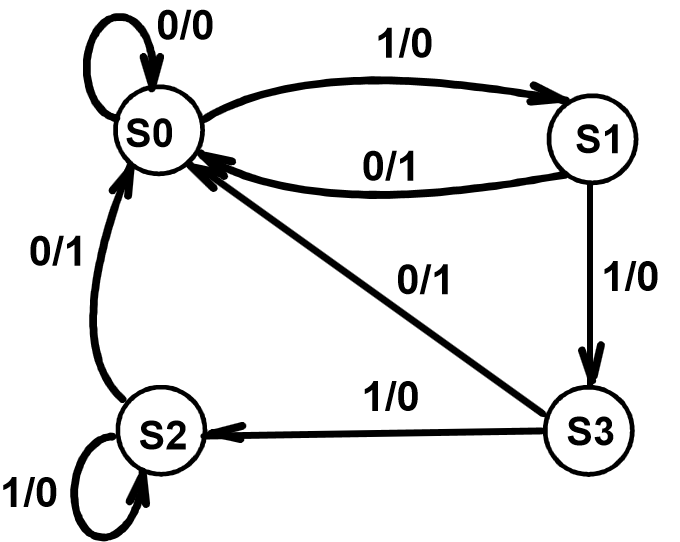
• S2, S3：输入0，转移至S0, 输出1；输入1，转移至S2，输出0，故等效

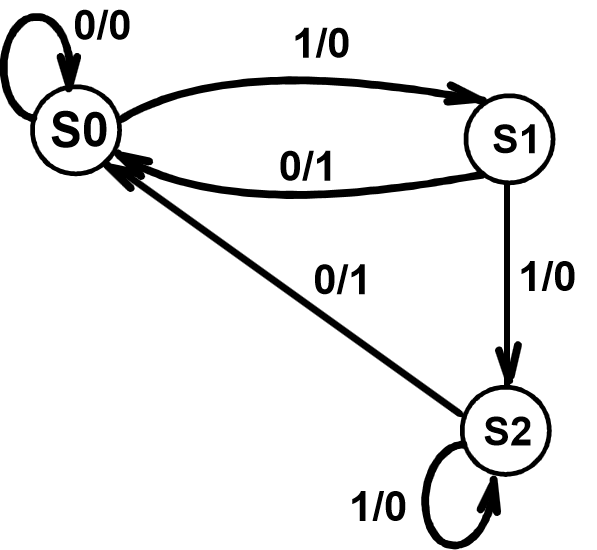
• S1, S2：输出0，转移至S2, 输出0；输入1，转移至S0，输出1，故等效

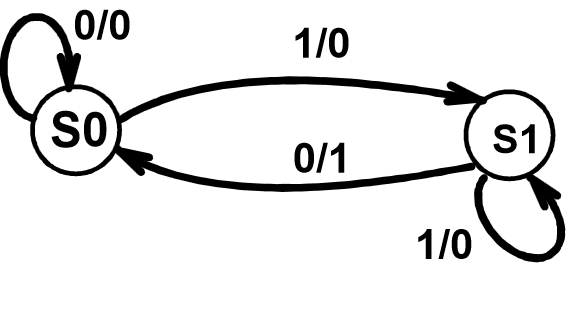
有限状态自动机(FSM)：

• Moore型：output depends only on state, 输出标记在圆圈内

  

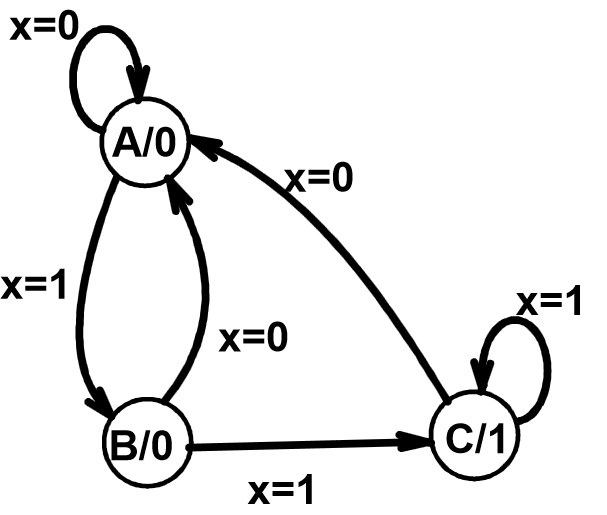
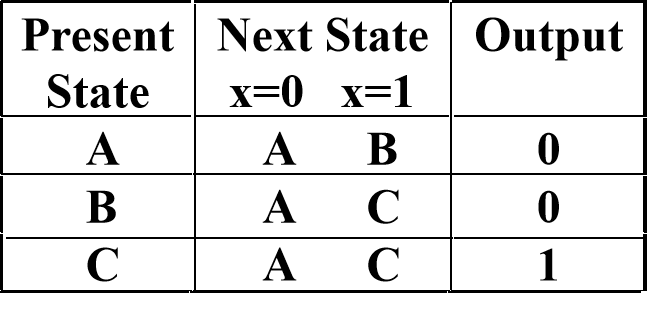
• Mealy型：output depends on state and input, 输出标记在弧上

  

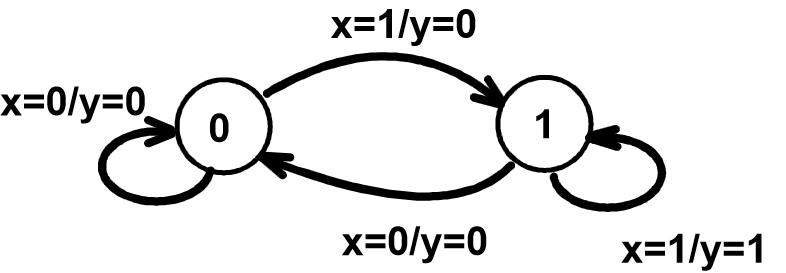
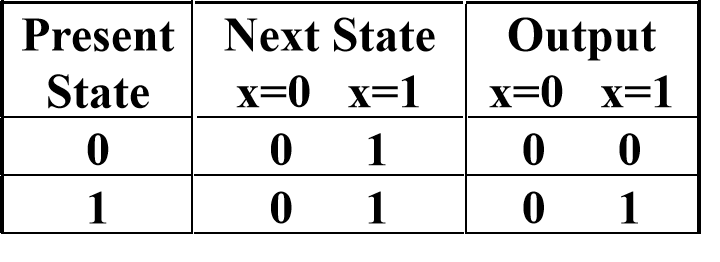
简化Mealy型：将部分输出放在圆圈内

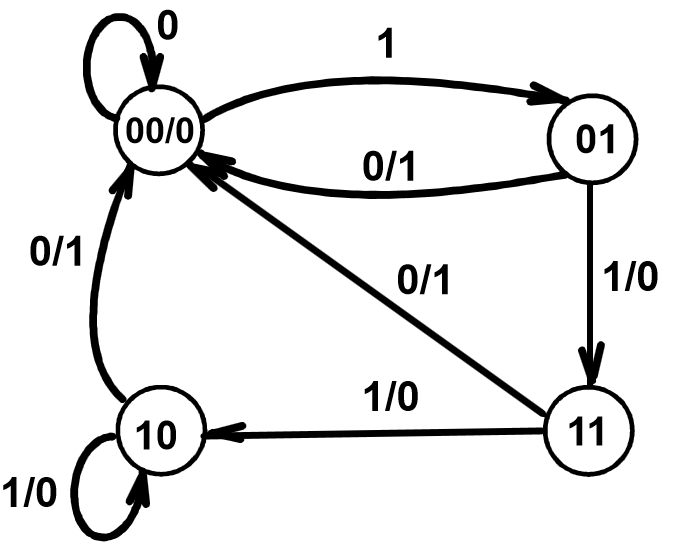
例：模5计数器

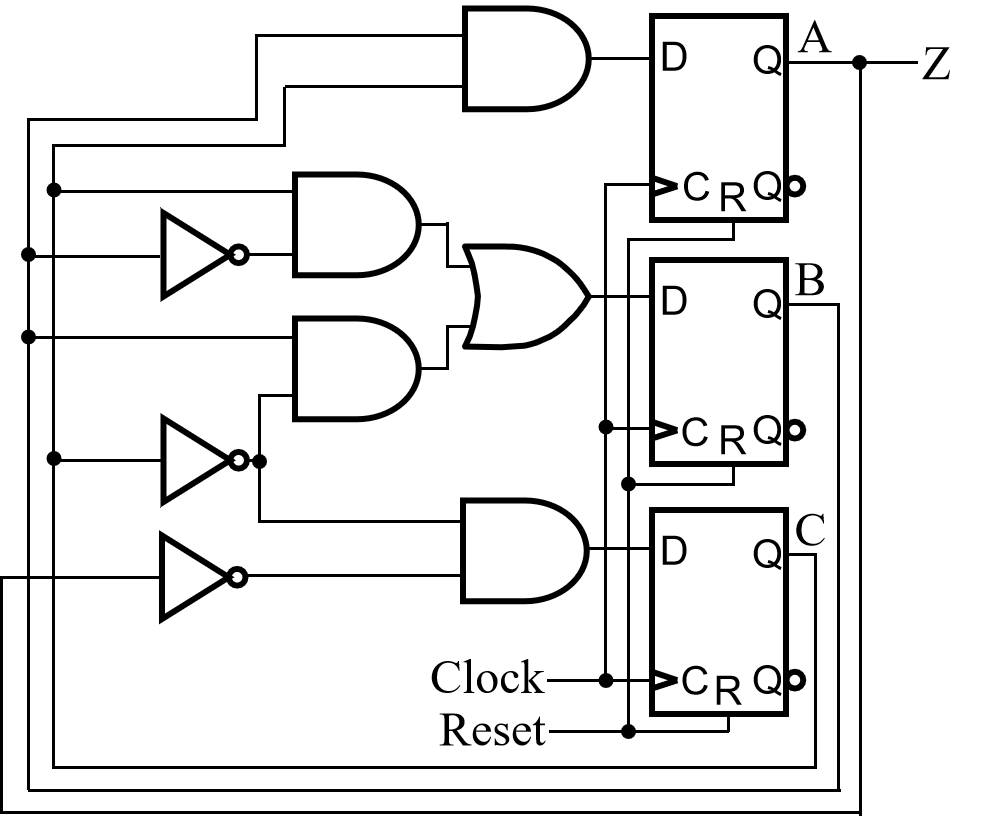
状态表：

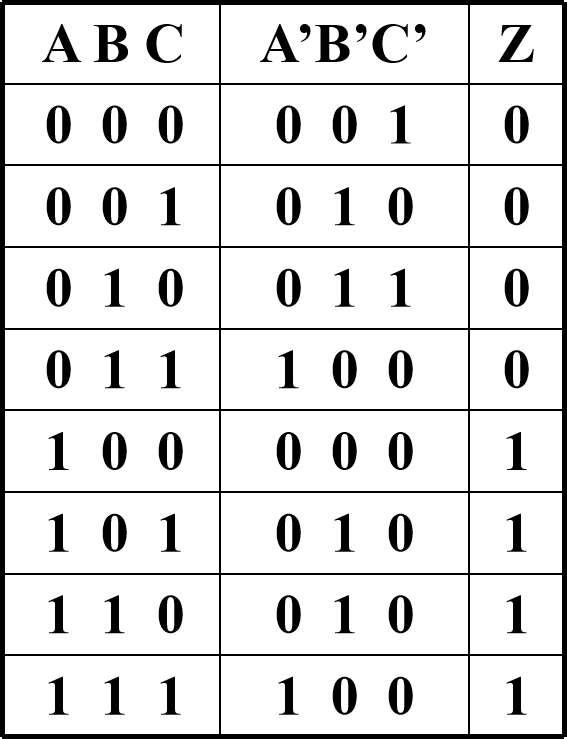
状态图：

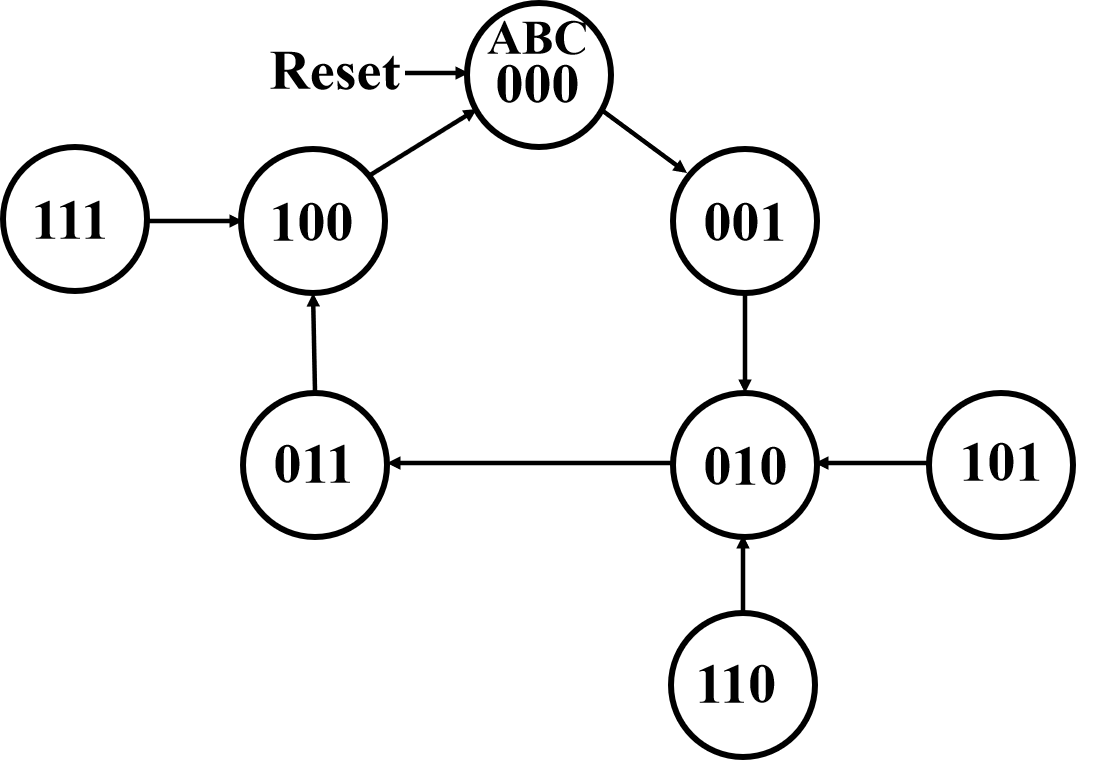
rst信号用于初值设定 死锁：当系统受到外部干扰跳到无效状态时可能引起死锁

graph LR;
A[101]<--->B[110]

状态表简化：

• 等效状态：设状态S1和S2是完全确定状态表中的两个状态,如果对于所有可能的输入序列，分别从状态S1和状态S2出发，所得到的输出响应序列完全相同，则状态S1和S2是等效的，记作(S1, S2), 或者说，状态S1和S2是等效对

• 判据：

  • 输出相同

  • 次态相同 / 交错 / 循环

    • 相同：\(S_i\equiv S_j\)

    

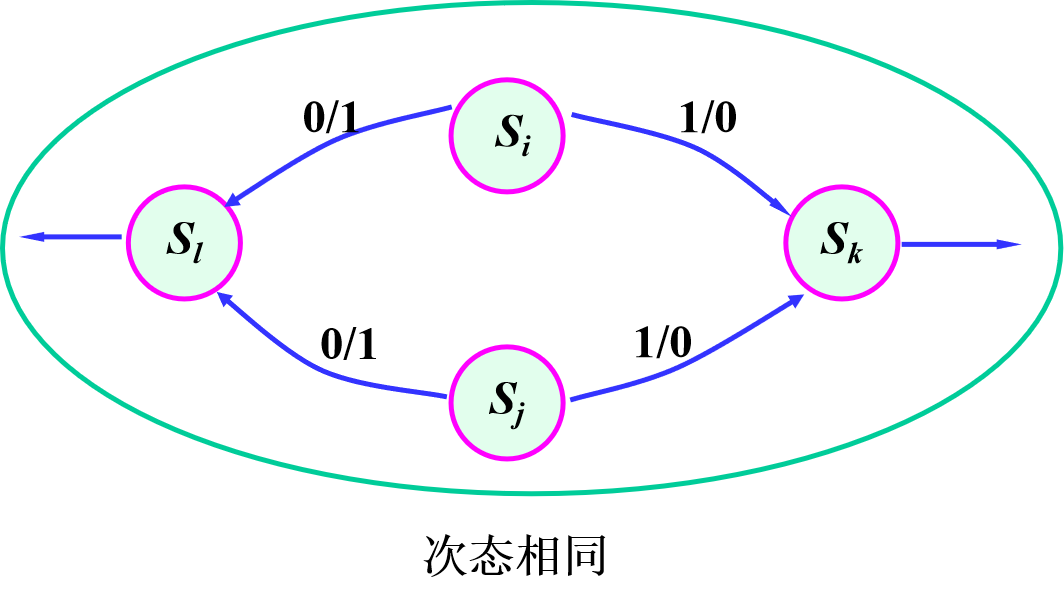
    • 交错：\(S_i\to S_j,S_j\to S_i\)

    

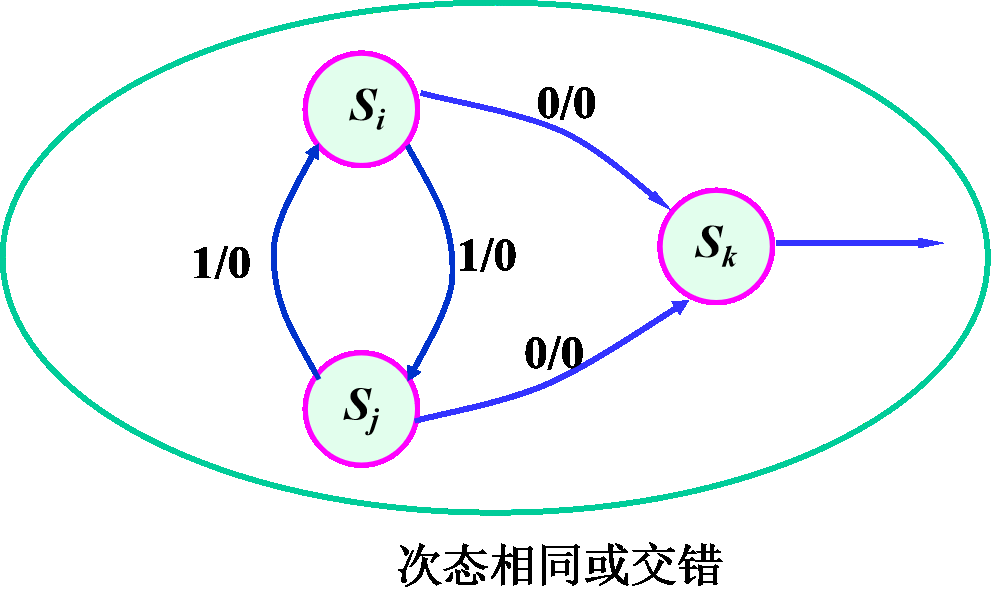
    \(S_i\equiv S_j\to S_k\equiv S_t\)

    

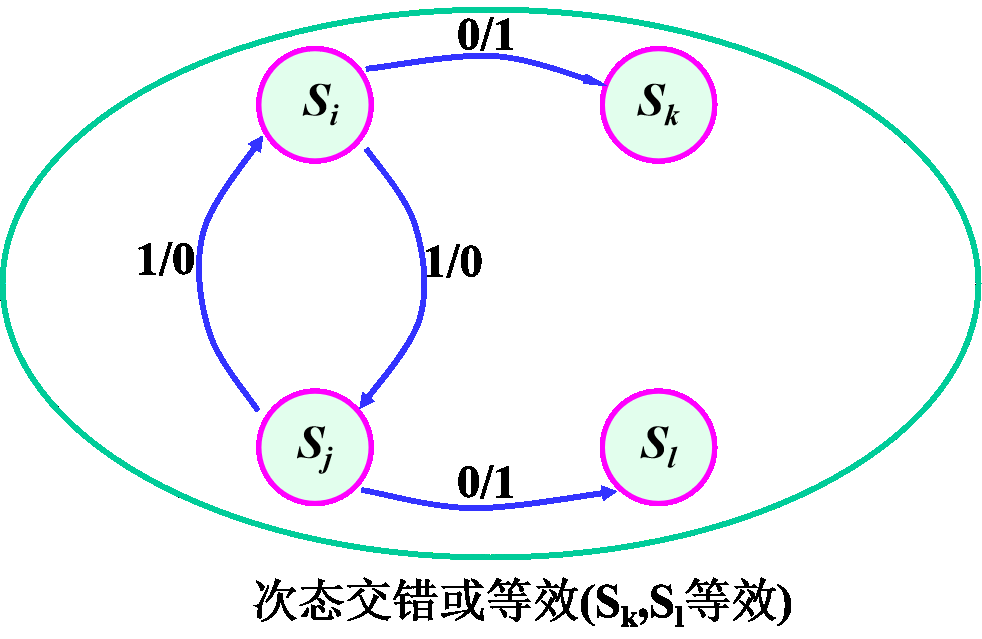
    • 循环：\(S_i\equiv S_j\to S_k\equiv S_t,S_k\equiv S_t\to S_i\equiv S_j\)

      

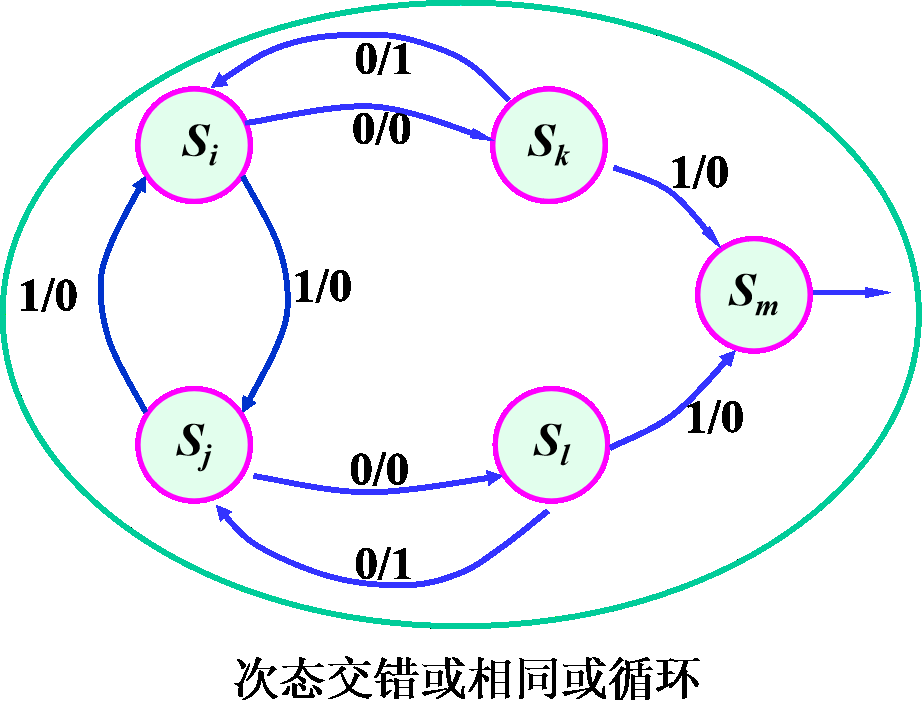
• 化简方法：

  • 观察法

  • 隐含表法

    

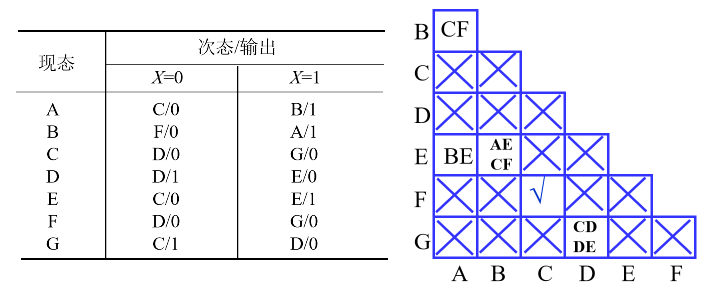
    • 由于CD、DE不等效，所以DG不等效，画斜线标志

    • 处于循环链中的每一个状态对都是等效状态对：

      

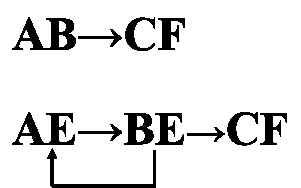
时钟参数：

• 占空比：\(\dfrac{t_{wH}}{t_{wH}+t_{wL}}\times100\%=50\%\)

• 边沿触发器：

  

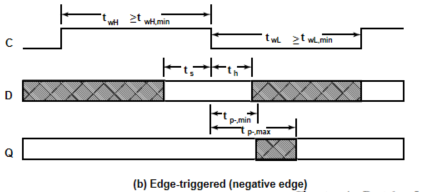
  • 建立时间\(t_s\)：触发信号==需要在建立时间前==触发，否则将不会被接收
  • 维持时间\(t_h\)：触发完成后信号不会被立刻改变
  • 传输延迟\(t_{px}\)：
    • \(t_{PHL}\)：High-to-Low
    • \(t_{PLH}\)：Low-to-High
    • \(t_{pd}\)：\(\max(t_{PHL},t_{PLH})\)
  • 主从触发器：

  

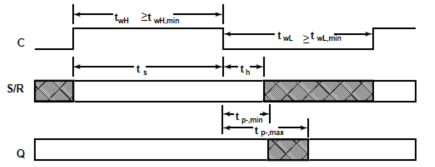
  • \(t_s\)为整个时钟脉冲的宽度（clk为高时输入信号不能改变——一次性采样）
  • \(t_h,t_{pd}\)

工作频率计算：触发时钟周期不能无限小，存在延迟；计算触发沿最小间隔

• 分析方法：将触发器拆成两部分

  

\[ t_p=t_{pd,FF}+t_{pd,COMB}+t_{slack}+t_s \]

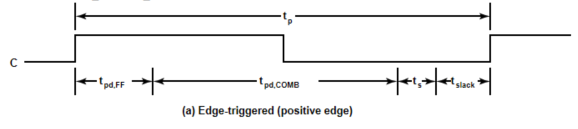
边沿触发器：

主从触发器：

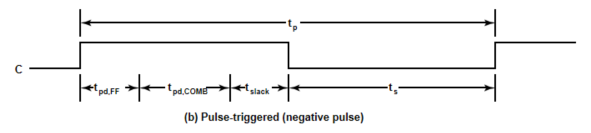
• \(t_{slack}\)：松弛时间，需大于等于0

结论：仅能缩短组合电路时间提升电路频率

最大工作频率：

\(t_p=t_{slack}+t_{pd,FF}+t_{pd,COMB}+t_s\geqslant\max(t_{pd,FF}+t_{pd,COMB}+t_{s})\)

例：\(t_{pd,FF}(\max)=1.0ns,t_s(\max)=0.3ns,f(clk)=250MHz\)

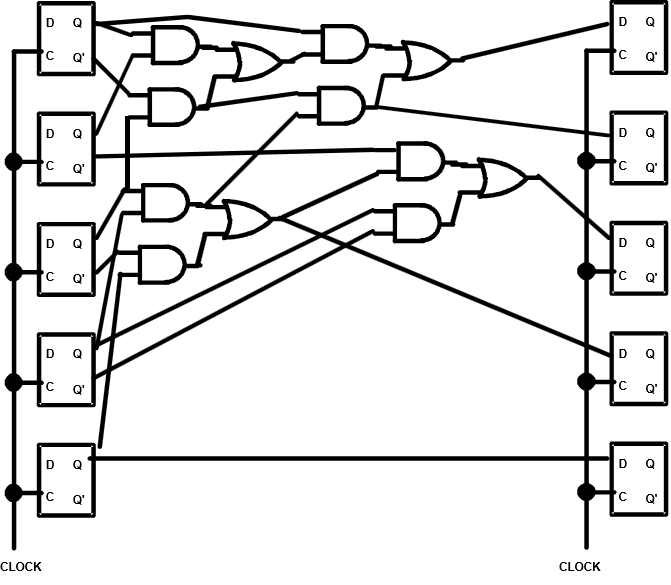
状态分配：为状态指定触发器的表达

• 例：

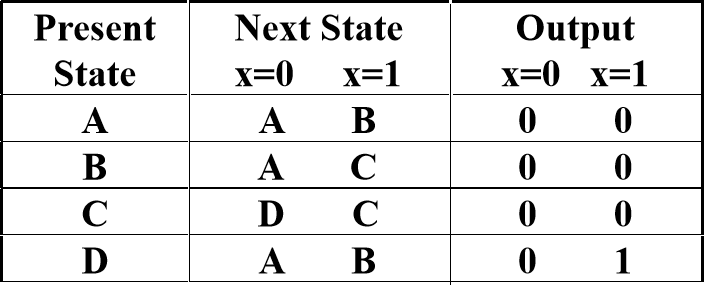
  分配A = 00, B = 01, C = 10, D = 11，得

  

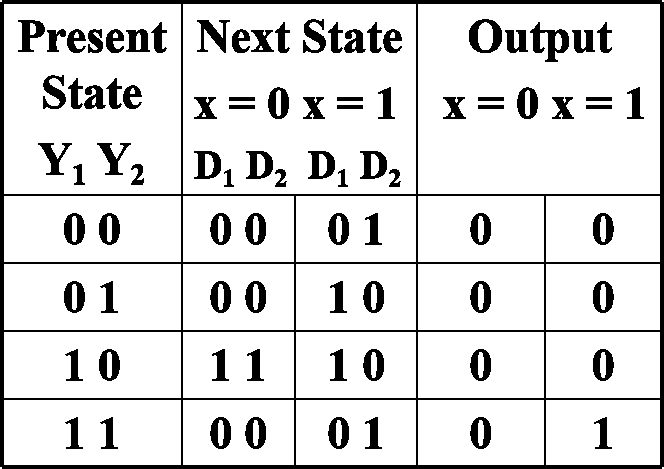
此处跳步：应先令次态为\(Y_1',Y_2'\)，由D触发器激励方程\(Q=D\)，得\(Y_1'Y_2'=D_1D_2\) 对SR触发器需根据\(Y_1'Y_2'\)倒推输出

\(D_1/D_2\)的值由\(Y_1,Y_2,X\)决定，交换三四行（变为格雷码序），构造卡诺图

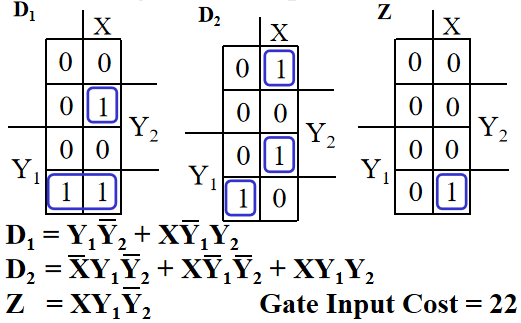
• 近似最优分配方案

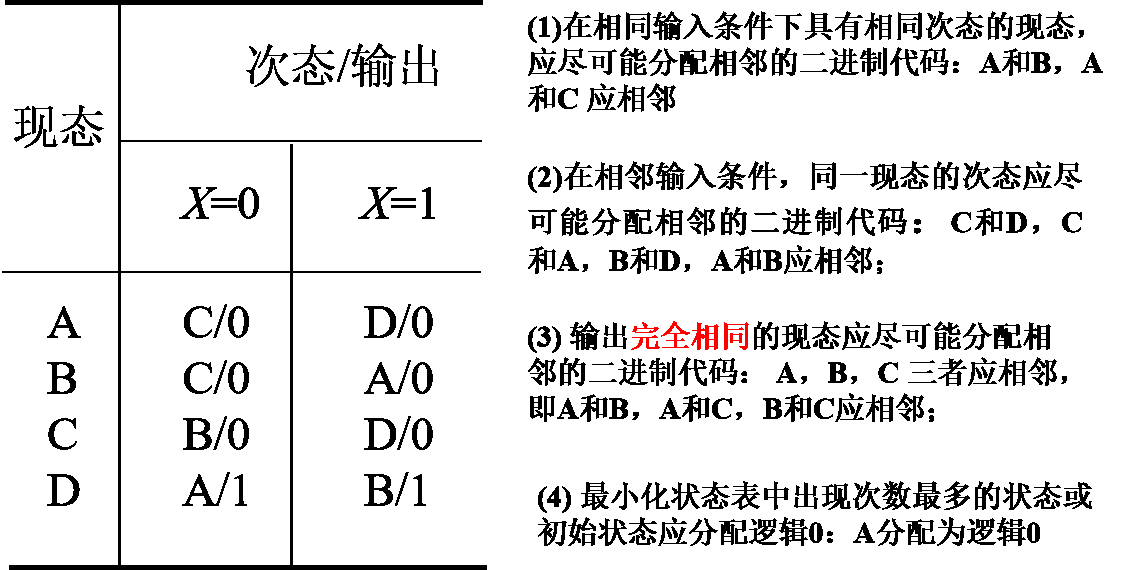
  1. 在相同输入条件下具有相同次态的现态，应尽可能分配相邻的二进制代码
  2. 在相邻输入条件，同一现态的次态应尽可能分配相邻的二进制代码
  3. 输出完全相同的现态应尽可能分配相邻的二进制代码
  4. 最小化状态表中出现次数最多的状态或初始状态应分配逻辑0

  • 例子

    

JK触发器：防止SR主从触发器S = R = 1的非法状态，J = K = 1时状态求反

• 问题：仍存在一次性采样的问题（保持 \(\to\) 求反 \(\to\) 保持）

• 实现：选择结构 + D触发器

  

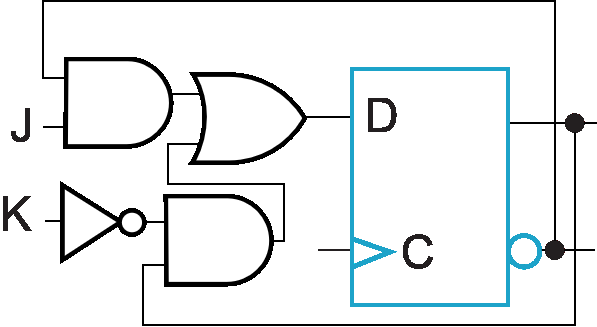
  • 保持：Q = D
  • 求反：\(\bar Q\) = D
  • 符号：

  

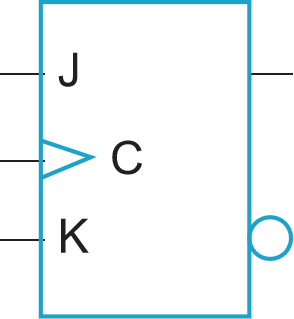
T触发器：T = 0保持，T = 1求反

• 实现：JK触发器，J = K = T

  • 问题：一次性采样

  • 解决：D触发器实现

    

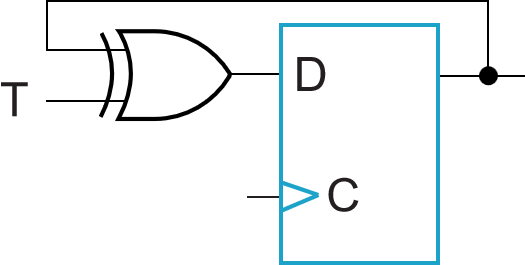
• 符号：

  

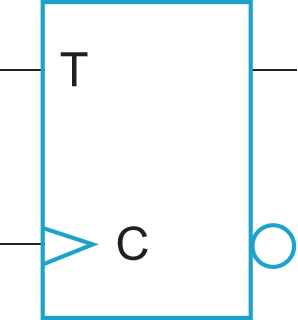
触发器行为描述：

• 特征表
• 特征方程
• 激励表

  分析时使用特征表，特征方程 设计时使用激励表

D触发器：

• 特征表：
• 特征方程：\(Q(t+1)=D\)
• 激励表：

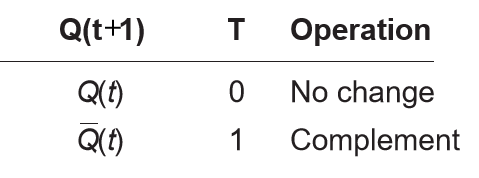
T触发器：

• 特征表：
• 特征方程：\(Q(t+1)=T\oplus Q\)
• 激励表：

SR主从触发器：

• 特征表：
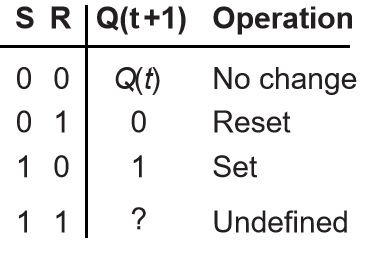
• 特征方程：\(Q(t+1)=S+\bar R Q\), \(S\cdot R=0\)
• 激励表：

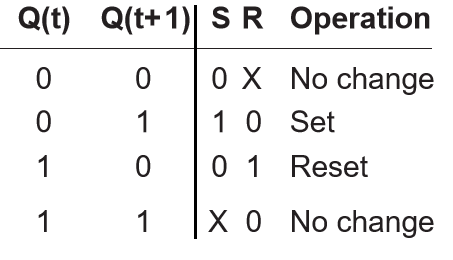
JK主从触发器：

• 特征表：
• 特征方程：\(Q(t+1)=J\bar Q+\bar KQ\)
• 激励表：