Arithmetic Functions
Iterative Combinational Circuits¶
问题:输入过多,无法使用真值表、卡诺图进行设计
特点:每一位运算操作相同
Iterative array takes advantage of the regularity to make design feasible
解决:design functional block for subfunction and repeat to obtain functional block for overall function
定义:
- Cell:子阵列
- Iterative array:一系列相连子阵列
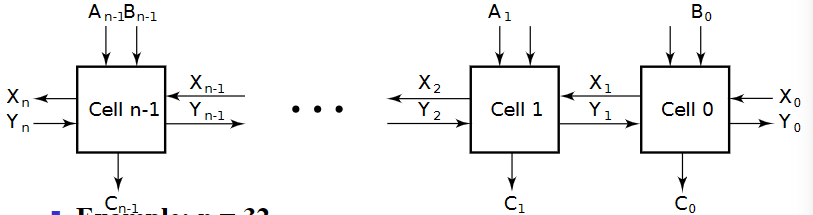
Functional Blocks: Addition¶
Half-Adder¶
定义:输入1bit X, Y, 输出进位标志C,本位和S
真值表:
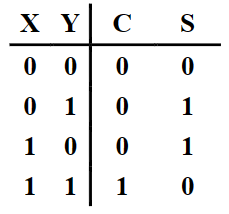
最常见实现:
- \(S=X\oplus Y,C=XY\)
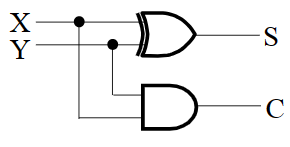
- \(S=(X+Y)\bar C,C=\overline{((\overline{XY}))}\)
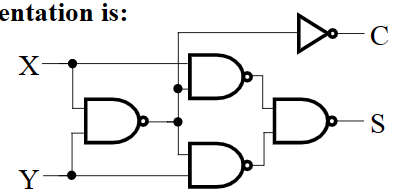
Full-Adder¶
定义:输入1bit X, Y, Z(上一位的进位),输出进位标志C,本位和S
真值表:
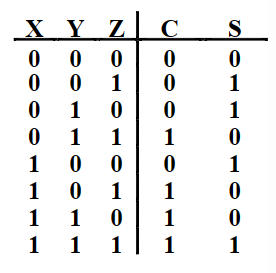
化简:由卡诺图得
奇函数:\(S=X\oplus Y\oplus Z\)
\(C=XY+Z(X+Y)=XY+Z(X\oplus Y)\)复用\(X\oplus Y\)
\(X\cdot Y\)称为进位生成器(当且仅当X=Y=1时产生进位) \(X\oplus Y\)称为进位传递(当X, Y有且仅有一个1时进位无法摆放,将被传递)
实现:
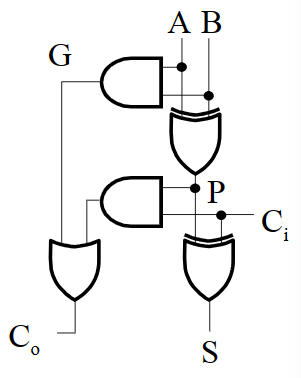
其中G为进位产生,P为进位传递,\(C_i\)为进位输入,\(C_o\)为进位输出
Binary Adders¶
实现:串连全加器(纹波加法器)
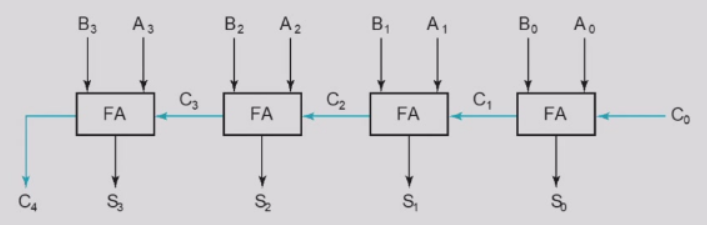
问题:进位传递存在延迟(\(C_n\)依赖\(C_{n-1}\))
思路:\(C_n\)依赖\(C_0\)
解决:Carry Lookahead
- 进位产生:\(C_{i+1}=G_i+P_iC_i\)
- 迭代:
- \(C_1=G_0+P_0C_0\)
- \(C_2=G_1+P_1C_1=G_1+P_1(G_0+P_0C_0)=G_1+P_1G_0+P_1P_0C_0\)
- \(C_3=G_2+P_2C_2=G_2+P_2(G_1+P_1G_0+P_1P_0C_0)=G_2+P_2G_1+P_2P_1G_0+P_2P_1P_0C_0\)
- 实现:
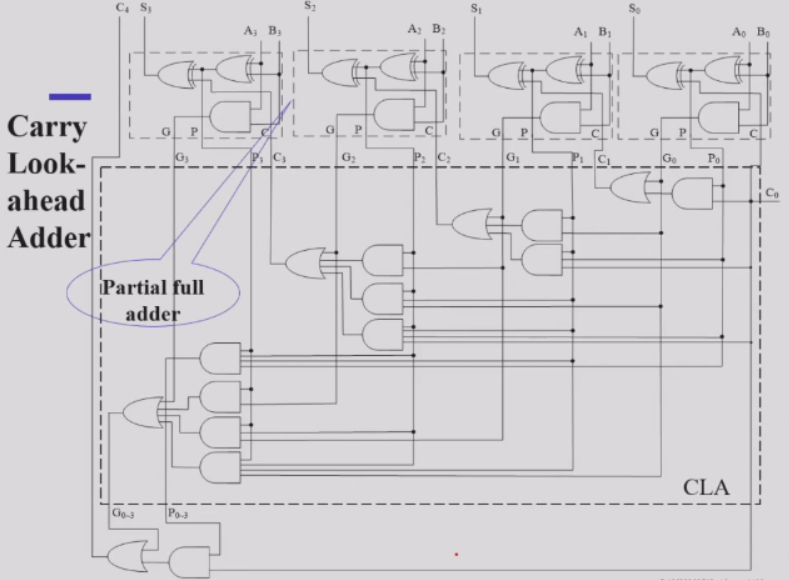
- 优势:进位传输延迟恒定2个门延迟
- 缺势:电路过于复杂,一个输入需给多个门提供信号
- 解决:串联CLA,形成纹波加法器
\(G_{0\sim3}=G_3+P_3G_2+P_3P_2G_1+P_3P_2P_1G_0\)
\(P_{0\sim3}=P_3P_2P_1P_0\)
\(C_4=G_{0\sim3}+P_{0\sim3}C_0\)
-
问题:存在进位传输延迟
-
解决:再套一层CLA

最长门路径:\(C_0\to C_4\to C_{12}\to C_{15}\),3次进入CLA:\(3\times2=6\),2次进入部分全加器:\(3+3=6\),共12个门
-
推广:64位加法器:4个16位加法器+CLA
-
-
- 解决:串联CLA,形成纹波加法器
\(G_{0\sim3}=G_3+P_3G_2+P_3P_2G_1+P_3P_2P_1G_0\)
\(P_{0\sim3}=P_3P_2P_1P_0\)
\(C_4=G_{0\sim3}+P_{0\sim3}C_0\)
Unsigned Subtraction¶
Complements:
- Diminished Radix Complement:\((r^n-1)-N\) (反码)
- Radix Complement:\(2^n-N\) (补码)
- 结论:补码 = 反码 + 1
- 求补码:
- 法一:反码 + 1
- 法二:保留lowbit, 其余求反
减法实现:被减数加上减数补码,若有进位,则说明结果为正;若无进位,则说明结果为负(补上的\(2^n\)被使用,说明是负数)
Signed Integers¶
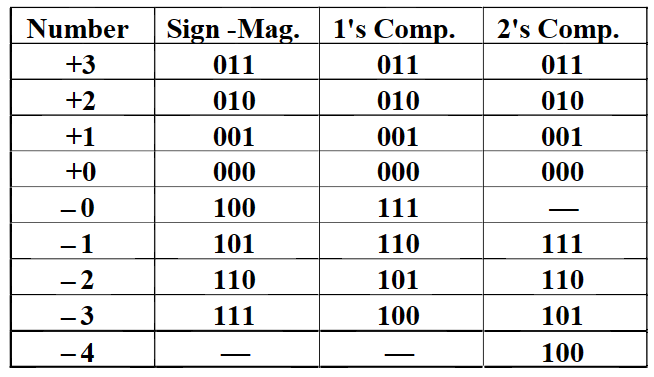
有符号真值 / 有符号反码存在\(\pm0\)
Signed-Magnitude Arithmetic¶
3 bit 表示:<第一位正负> <加/减> <第二位正负>
Signed-Complement Arithmetic¶
思路:减去一个数等于加上其补码
2’s Complement Adder/Subtractor¶
输入:\(A,B,S\),S=1表示做减法
思路:\(S=1\)时需求\(B\)反码,直接与\(B\)做异或,将1加到\(C_0\)处
实现:
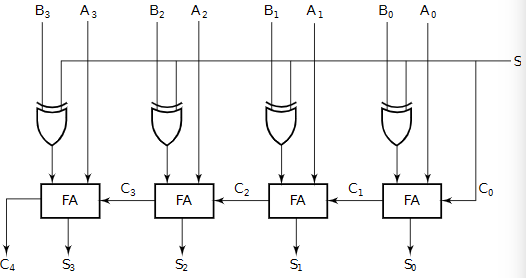
溢出处理:
- 同号相加:正 + 正 = 正 时不溢出
- 异号相减:正 - 负 = 正 时不溢出
- 问题:需要涉及四个位
- 解决:正数运算后仍为正数不溢出,负数运算后仍为负数不溢出,即原符号与得到的符号相同时不溢出,故仅需判断\(V=C_n\oplus C_{n-1}\)
Other Arithmetic Function¶
Incrementing / Decrementing¶
约简:当某一个运算数固定时,可简化电路
-
操作:从全加器出发,固定门输入,从而部分门的行为确定,从而实现门的简化
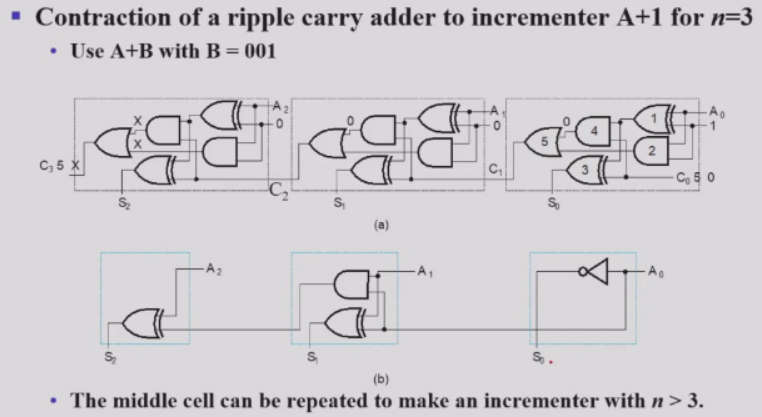
-
应用:实现计数器
Multiplication / Division by \(2^n\)¶
左移:填充0
右移:填充符号位
Arithmetic Logic Unit (ALU)¶
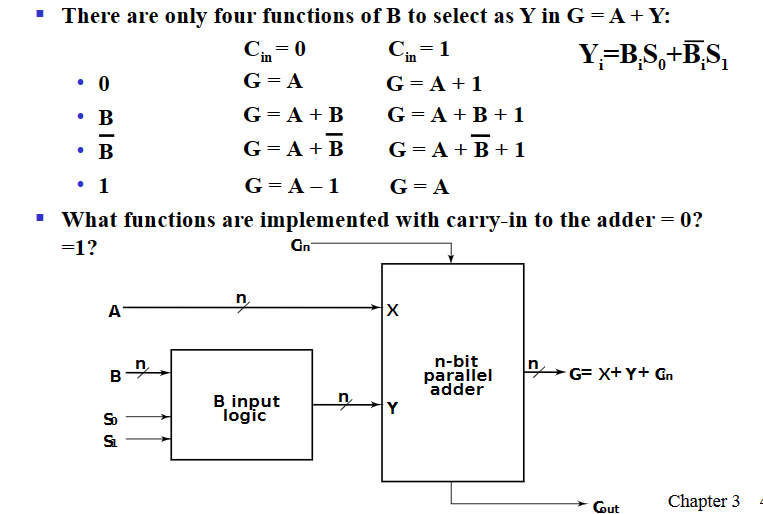
实现传输,自增自减,加减法操作