Gate Circuits and Boolean Equations

二进制变量：0 / 1

逻辑操作符：

  • 与(AND)：\(\cdot\)
  • 或(OR)：\(+\)
  • 非(NOT)：\(\bar{},\quad',\quad\sim\)

真值表：a tabular listing of the values of a function for all possible combinations of values on its arguments

X Y Z = X·Y
0 0 0
0 1 0
1 0 0
1 1 1

实现：

  1. 开关电路：

    • 输入：1 - 闭，0 - 开
    • 输出：1 - 亮，0 - 灭
    • 非门：1 - 开，0 - 闭
    • 与门：串联
    • 或门：并联

      一个电路的输出作为另一个电路的输入：继电器 问题：体积庞大；发热严重；易损坏

  2. CMOS管：

    • 栅极 -o
    • PMOS：常闭
    • NMOS：常开
      与非，或非，非门的电路实现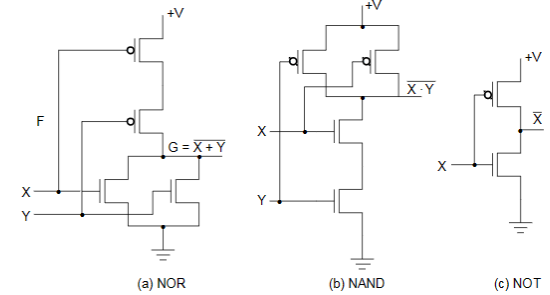： image.png|350

      输入可以短接，输出不可短接（导致短路） 在某些特殊条件下输出可以短接

权衡：性能与成本（晶体管个数）

制程：栅极的宽度 -> 晶体管大小 -> 晶圆大小

表示：

  • 逻辑符号： image.png|500
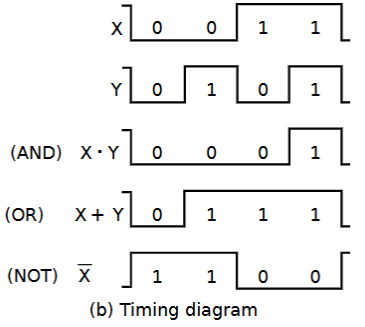
  • 波形图： image.png|300
    • 横坐标：时间
    • 纵坐标：输出的信号

门延迟（t_G）：In actual physical gates, if one or more input changes causes the output to change, the output change does not occur instantaneouly.

影响：电路最高工作频率上限

逻辑函数表示：

  • 真值表（唯一）
  • 函数（不唯一）
  • 电路图（不唯一）

布尔代数：

  • \(X+0=X,X+1=1,X\cdot0=0,X\cdot1=1\)
  • \(X+X=X,X\cdot X=X\)
  • \(X+\overline X=1,X\cdot\overline X=0\)
  • \(\overline{\overline X}=X\)
  • 交换律：\(X+Y=Y+X,XY=YX\)
  • 结合律：\((X+Y)+Z=X+(Y+Z),(XY)Z=X(YZ)\)
  • 分配率：\(X(Y+Z)=XY+XZ,X+YZ=(X+Y)(X+Z)\)

对偶：\(\cdot\leftrightarrow+,0\leftrightarrow1\)，并保证运算优先级不变

自对偶：对偶＝自身

定理：

  • 吸收律：\(A+A\cdot B=A\)
  • 一致律：\(AB+\overline AC+BC=AB+\overline AC\)
  • 最小律：\(A\cdot B+\overline A\cdot B=B\)
  • 简化律：\(A+\overline A\cdot B=A+B\)
  • 德摩根律：\(\overline{X+Y}=\overline X\cdot\overline Y,\overline{X\cdot Y}=\overline X+\overline Y\)
    • 证明：即要证\(X+Y,\overline X\cdot\overline Y\)互反，只要证\((X+Y)\cdot(\overline X\cdot\overline Y)=0,(X+Y)+(\overline X\cdot\overline Y)=1\)

反函数：\(\cdot\leftrightarrow+,0\leftrightarrow1,x\leftrightarrow\overline x\)，并保证运算优先级不变

标准型：SOM (sum of minterms), POM (product of maxterms)

  • 最小项和最大项：
    • 最小项：包含所有变量或反变量的积式
    • 最大项：包含所有变量或反变量的和式
    • 编号：使得最小项唯一为1 / 最大项唯一为0 的取值组合，如\(\overline xy\)取1时\(x=0,y=1\)，为第\((01)_2=1_{10}\)项
    • 性质：\(M_i=\overline{m_i},m_i=\overline{M_i}\)
  • 真值表：作为最小项的或（最大项的积）
  • 与或表达式转换：补项，如\(AB\to AB(C+\overline C)\)
  • 简写：\(F(A,B,C)=\sum_m(1,4,5,6,7)\)
  • SOM, POM互化：\(F(x,y,z)=\sum_m(1,3,5,7)=\prod_M(0,2,4,6)\)\(\Rightarrow\overline F(x,y,z)=\prod_M(1,3,5,7)=\sum_m(0,2,4,6)\)
  • SOP(Standard Sum-of-Products), POS(Standard Product-of-Sums)
    • 两极电路：先与门后或门 / 先或门后与门，效率最高
  • SOM \(\to\) SOP

问题：

  • How can we attain a “simplest” expression?
  • Is there only one minimum cost circuit?