Circuit Optimization

目标：获得给定函数的最简实现

衡量标准：

• Literal Cost (L)
  • 定义：出现过的所有变量的个数
  • 例：\(F=ABCD+\overline{ABCD}\)，L = 8
• Gate Input Cost (G), Gate input cost with NOTs (GN)
  • 定义：G：L + 出现的项个数（不含单变量，输出）GN：G + 非门个数（一个变量计算一次）
  • 例：\(F=BD+A\overline BC+A\overline{BD}+AB\overline C\)，G = 11 + 4 = 15 GN = 15 + 3 = 18
  • 非门一般无需计算（前部电路可提供），但内部电路的非门需计算
• 与电路对应：

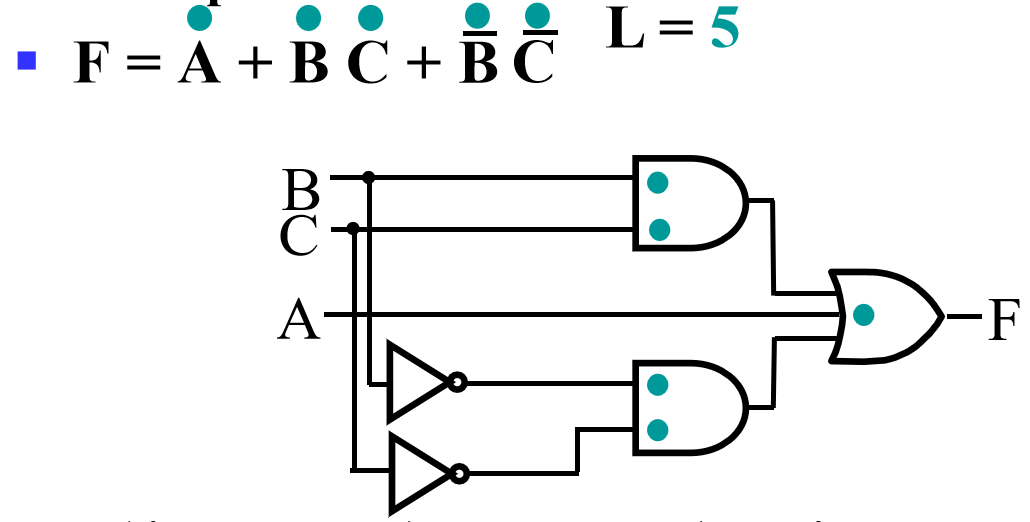
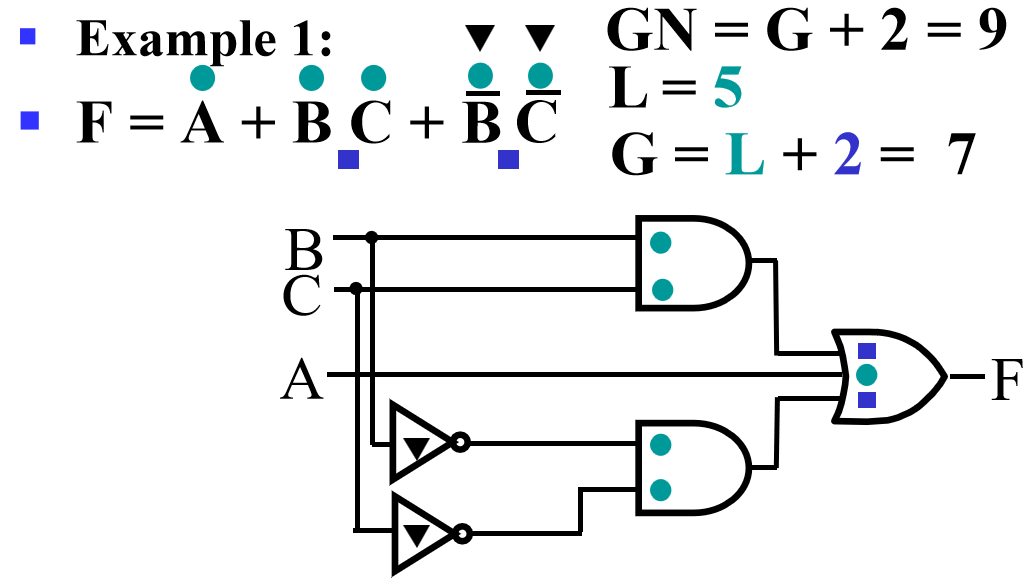
卡诺图 (K-map)

排布：相邻两个格子只有一处差异

双变量卡诺图：

	y=0	y=1
x=0	\(m_0=\bar x\bar y\)	\(m_1=\bar xy\)
x=1	\(m_2=x\bar y\)	\(m_3=xy\)

三变量卡诺图：列序为格雷码

	yz=00	yz=01	yz=11	yz=10
x=0	\(m_0=\bar x\bar y\bar z\)	\(m_1=\bar x\bar yz\)	\(m_3=\bar xyz\)	\(m_2=\bar xy\bar z\)
x=1	\(m_4=x\bar y\bar z\)	\(m_5=x\bar yz\)	\(m_7=xyz\)	\(m_6=xy\bar z\)

图示：

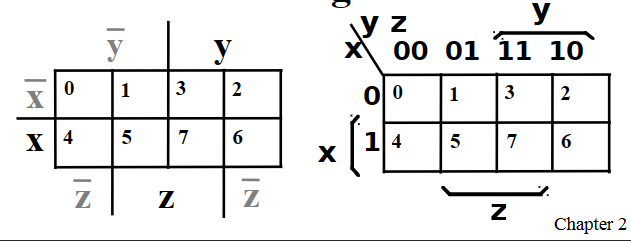
\(x\bar z,xz\)也相邻，理解为将卡诺图卷起为柱

四变量卡诺图：行序列序均为格雷码

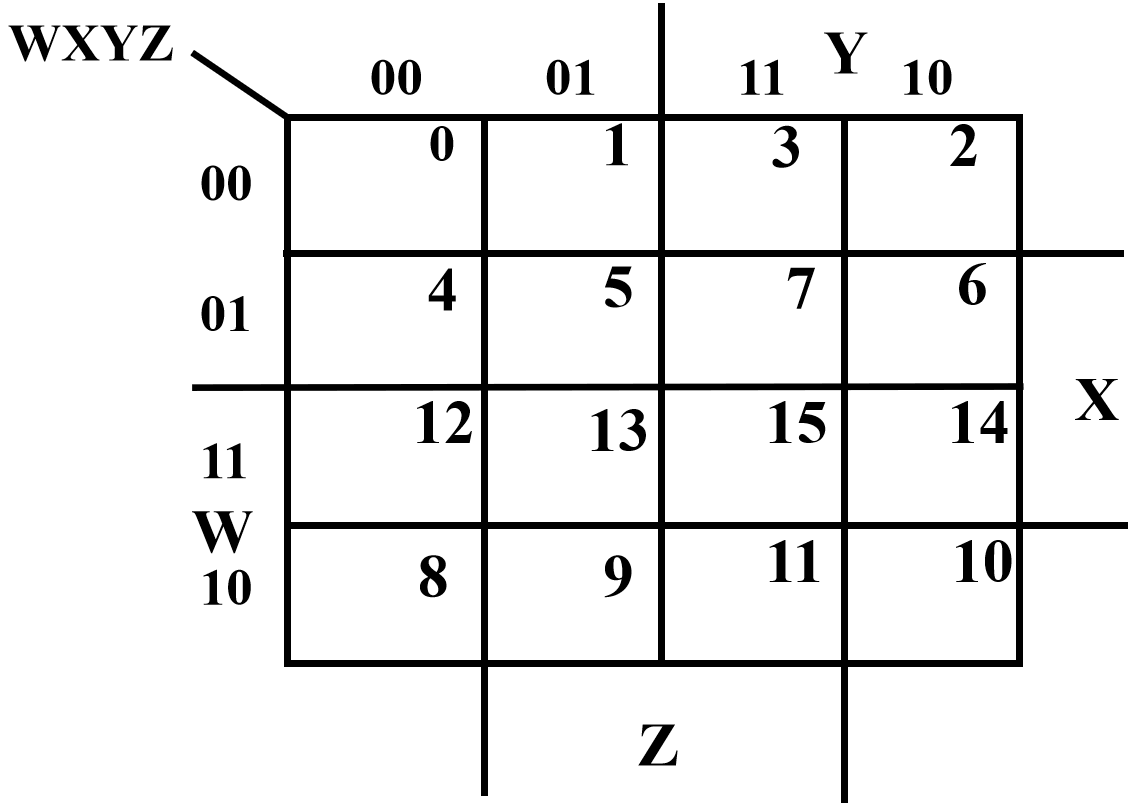
\(\bar x\bar z\)区域：卷起为球

五变量卡诺图：使用两个四变量卡诺图

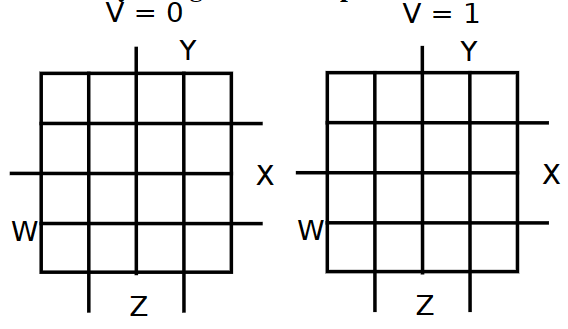
五变量及以上的卡诺图难以找圈，一般变量数不超过四个

化简：

• 将相邻的2，4或8个变量圈起，消去变化的变量
• 先圈最大的圈，用尽可能大的圈去圈（减少变量数，圈可重叠）

无关项：从不会出现的输入，从不会使用的输出

表示：d(i), 在卡诺图上用 x 表示；被圈起时x作1，不圈作0

寻找POS：先找SOP，再求反

系统化化简方法：

1. 寻找质蕴含项：从最大可圈开始，直到圈出所有最小项
2. 寻找必要质蕴含项：含有只被圈一次的最小项的圈

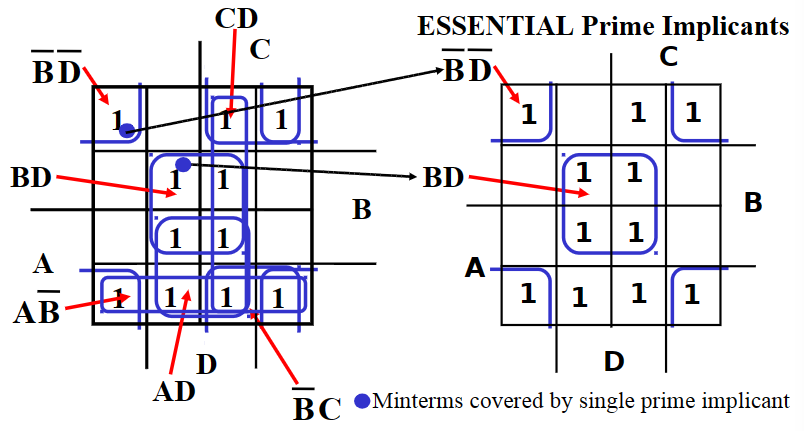
多级门电路优化：通过提取公因式，降低G

电路级数：输入到输出的最长路径长度