神经网络参数优化

目的：使得神经网络能够将给定输入数据映射到所期望的输出语义空间，完成分类识别等任务

本质：神经网络参数优化是一个监督学习的过程

操作：模型利用反向传播算法将损失函数计算所得误差从输出端出发，由后向前传递给神经网络中每个单元，然后通过梯度下降算法对神经网络中的参数进行更新；当迭代达到一定轮次或准确率达到一定水平时，则可认为模型参数已被优化完毕

损失函数：计算模型预测值与真实值之间的误差

• 均方误差损失函数：\(\text{MSE}=\dfrac{1}{n}\sum_{i=1}^n(y_i-\hat y_i)^2\)
• 交叉熵损失函数：\(H(y_i,\hat y_i)=-y_i\times\log_2\hat y_i\)

梯度下降：使损失函数最小化的方法

• 梯度：\(\dfrac{\text{d}f(x)}{\text{d}x}=\lim\limits_{h\to0}\dfrac{f(x+h)-f(x)}{h}\quad f(x+\Delta x)-f(x)\approx(\nabla f(x))^\mathsf T\Delta x\)
• 操作：\(x\leftarrow x-\eta\nabla f(x)\)
• 方法：
  • 批量梯度下降：在整个训练集上计算损失误差（数据集较大导致内存不足）
  • 随机梯度下降：使用每个数据计算损失误差（波动大难收敛；可跳出局部最优）
  • 小批量梯度下降

误差反向传播：利用损失函数来计算模型预测结果与真实结果之间的误差以优化调整模型参数

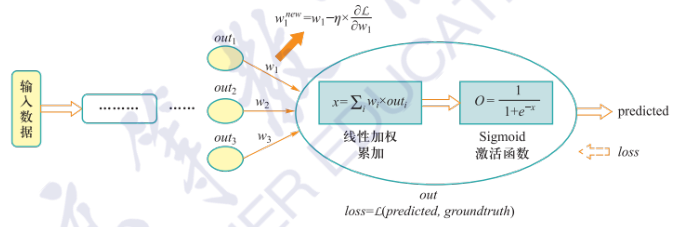$$ \dfrac{\partial\mathcal L}{\partial w_1}=\dfrac{\partial\mathcal L}{\partial o}\dfrac{\partial o}{\partial x}\dfrac{\partial x}{\partial w_1}\quad w_1^\text{new}=w_1-\eta\times\dfrac{\partial\mathcal L}{\partial w_1} $$