循环神经网络

应用：处理序列数据（文本句子、视频帧）时采用的网络结构

本质：希望模拟人所具有的记忆能力，在学习过程中记住部分已经出现的信息，并利用所记住的信息影响后续节点的输出

网络模型：在处理数据过程中构成循环体，在$t$时刻读取当前输入数据$x_i$和前一时刻输入数据$x_{i-1}$所对应的隐式编码结果$h_{i-1}$，一起生成$t$时刻的编隐式码结果$h_i$

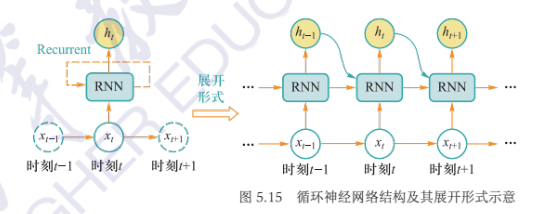
表示：$h_i=\Phi(U\times x_i+W\times h_{i-1})$
展开：按照时间展开得到与前馈神经网络相似的网络结构，沿时间反向传播算法 $$ h_i=\Phi(U\times x_i+W\times h_{i-1})=\Phi(U\times x_i+W\times\Phi(U\times x_{i-1}+W\times \Phi(U\times x_{i-1}+\cdots))) $$
问题：梯度消失（叠加激活函数导致梯度越来越小） $$ \dfrac{\partial E_t}{\partial W_x}=\sum_{i=1}^t\dfrac{\partial E_t}{\partial O_t}\dfrac{\partial O_t}{\partial h_t}\left(\prod_{j=i+1}^t\dfrac{\partial h_j}{\partial h_{j-1}}\right)\dfrac{\partial h_j}{\partial W_x} $$
解决：LSTM

长短时记忆网络：

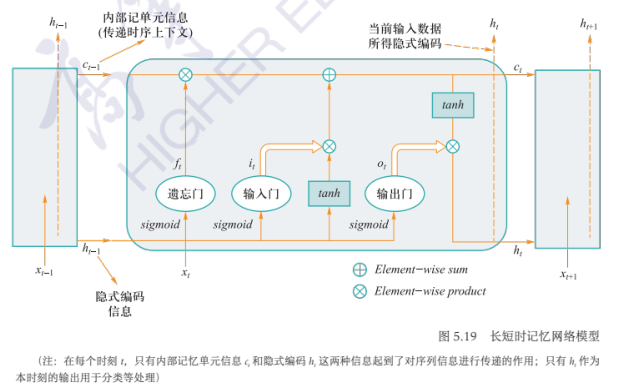
image.png|500

对$c_t=f_t\odot c_{t-1}+i_t\cdot \tanh(W_{xc}x_t+W_{hc}h_{t-1}+b_c)$求导，结果为 $\dfrac{\partial c_t}{\partial c_{t-1}}=f_t+\dfrac{\partial f_t}{\partial c_{t-1}}\times c_{t-1}+\cdots$ 即梯度不会消失