因果推理

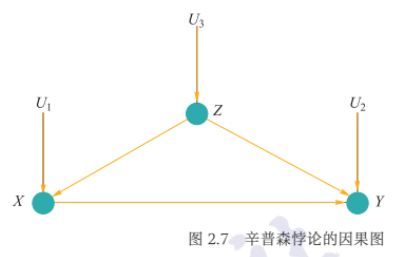
辛普森悖论：在某些情况下，忽略潜在的“第三个变量”可能会改变已有的结论

克服辛普森悖论：厘清真假关联

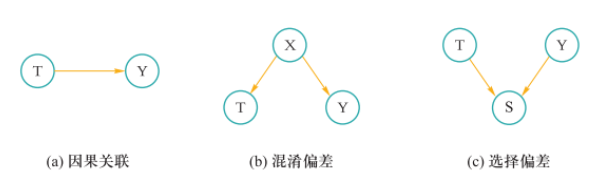
关联： image.png|400

  • 因果关联：一个变量是另一个变量的原因
  • 混淆关联：两个变量存在共同的原因变量
  • 选择关联：两个变量存在共同的结果变量

联合概率分布：\(P(x_1,x_2,\cdots,x_d)=\prod\limits_{j=1}^dP(x_j\vert\ x_{pa_{\set j}})\)

干预：改变明确存在关联关系的某变量取值，研究变量取值改变对结果变量的影响

"do"算子：计算当系统中一个变量取值发生变化、其它变量保持不变时，系统输出结果是否变化。\(P(Y=y\vert do(X=x))\)表示对\(X\)进行干预，固定其值为\(x\)时，\(Y=y\)的概率

因果效应差：为考虑用药(X)对恢复(Y)的效应查，对X进行操控有

image.png|300 \(P(Y=1|do(X=1))-P(Y=1|do(X=0))\)

计算\(P(Y=1|do(X=1))\)时，将指向X的边移除得到操纵图\(P_m\)

image.png|300 则\(P(Y=y|do(X=x))=P_m(Y=y|X=x)\).

性质：

  1. \(P(Z=z)=P_m(Z=z)\)
  2. \(P(Y=y|X=x,Z=z)=P_m(Y=y|X=x,Z=z)\)

化简：

\[ \begin{array}{l} P(Y=y|do(X=x))=P_m(Y=y|X=x)\\ =\sum\limits_zP_m(Y=y|X=x,Z=z)P_m(Z=z|X=x)\\ =\sum\limits_zP_m(Y=y|X=x,Z=z)P_m(Z=z)\\ =\sum\limits_zP(Y=y|X=x,Z=z)P(Z=z) \end{array} \]

结论：因果效应：给定因果图G，PA表示X的父节点集合，则X对Y的因果效应为\(P(Y=y|do(X=x))=\sum\limits_{z}P(Y=y|X=x,PA=z)P(PA=z)\)