alpha-beta搜索

剪枝方法：在最小最大搜索中可减少被搜索的结点数

例：

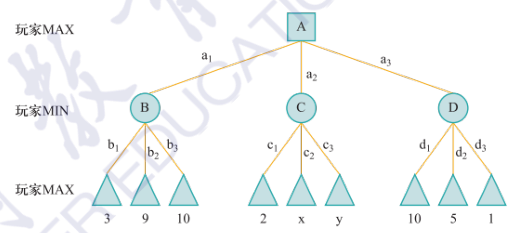
\(minimax(A)=\max(\min(3,9,10),\min(2,x,y),\min(10,5,1))=\max(3,\min(2,x,y),1)\)

而\(\min(2,x,y)\leqslant2\)，可直接剪枝。

• 基于MIN节点反馈收益进行剪枝

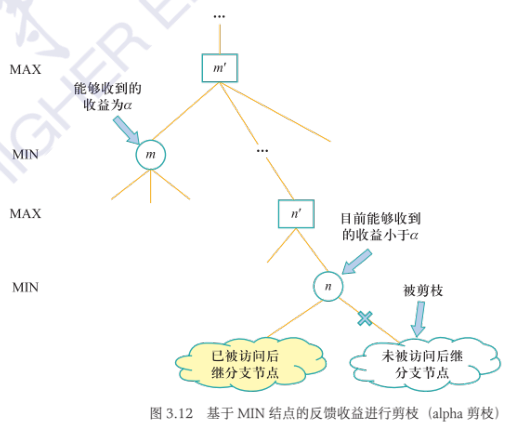
• 基于MAX节点反馈收益进行剪枝

AlphaBetaDecision: (MAX最优动作a*)
    v,a* ← MaxValue(s,-∞, +∞)

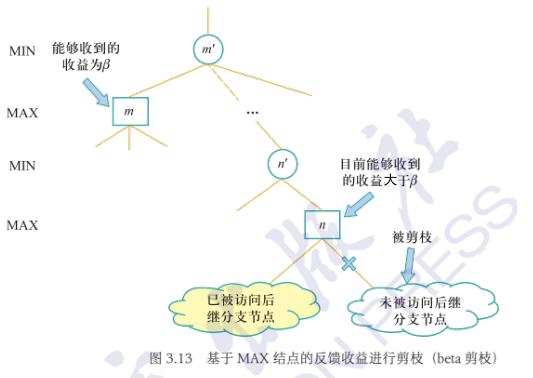
MaxValue:
    if terminal_test(s) then return utility(s), null
    v ← -∞
    a* ← null
    foreach a∈actions(s) do
        v', a' ← MinValue(result(s,a), α, β)
        if v' > v then
            v' ← v
            a* ← a
        end
    α ← max(α, v)
    if α ≥ β then return v, a*
end

MinValue:
    if terminal_test(s) then return utility(s), null
    v ← +∞
    a* ← null
    foreach a∈actions(s) do
        v', a' ← MaxValue(result(s,a), α, β)
        if v' < v then
            v' ← v
            a* ← a
        end
    β ← min(β, v)
    if α ≥ β then return v, a*
end

原理：

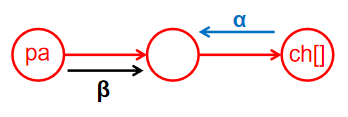
以当前节点为MAX层为例，则pa为MIN层，当前将选择小于\(\beta\)的节点，ch为MIN层。

每次根据新计算出的ch节点值更新该层的\(\alpha\)值（\(\alpha\)在更新过程中不减），更新完毕后立即检查是否符合\(\beta\)值的要求，即\(\alpha<\beta\)，即该节点仍具有为pa提供更小答案的潜力；否则，若\(\alpha\geqslant\beta\)，由于\(\alpha\)不减，将无法提供更小答案，将被父节点遗弃，此时未扩展完的子节点将被剪枝。

简而言之，每个节点从子节点进行答案的更新，又受到父节点的监督；当两种策略发生交叠时进行剪枝。