A-star搜索

A*搜索：在评价函数中考虑从起始节点到当前节点的路径代价 \(f(n)=g(n)+h(n)\)

其中\(g(n)\)为起始节点到节点\(n\)代价（当前最小代价）

例：

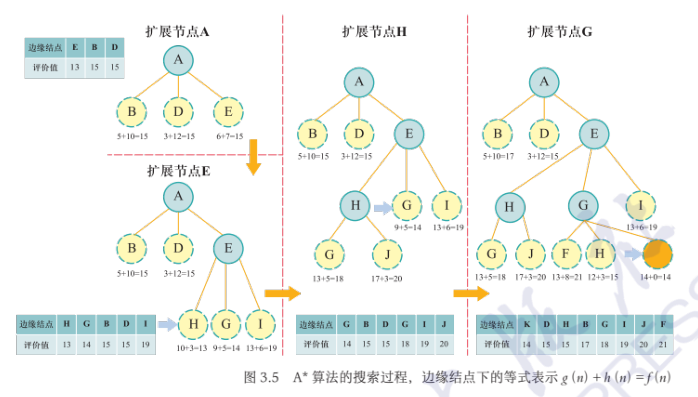
处处最优 \(\Rightarrow\) 全局最优

性能分析：A*算法的完备性和最优性取决于搜索问题和启发函数的性质

• 记号：
  • \(h(n)\)：结点n的启发函数取值（直线距离）
  • \(g(n)\)：从起始结点到结点n所对应路径的代价
  • \(f(n)\)：结点n的评价函数取值
  • \(c(n,a,n')\)：从结点n执行动作a到达结点n'的单步代价
  • \(h^*(n)\)：从结点n出发到达终止结点的最小代价（实际距离）
• 可容性：\(\forall n:h(n)\leqslant h^*(n)\)，即启发函数不会过高估计从节点\(n\)到终止节点所应该付出的代价（即估计代价小于等于实际代价）
• 一致性： \(h(n)\leqslant c(n,a,n')+h(n')\)三角不等式

graph LR;
A[n]--c---B["n'"]
B---C[E]
A---C

定理1：一致 \(\Rightarrow\) 可容

证：设最短路为\(n_1\to n_2\to\cdots\to K\) \(h(K)=0\)

\(\because\)一致

\(\therefore h(n_1)\leqslant h(n_2)+c(n_1,a_1,n_2)\leqslant h(n_3)+c(n_2,a_2,n_3)+c(n_1,a_1,n_2)\)\(\leqslant\cdots\leqslant c(n_1,a_1,n_2)+c(n_2,a_2,n_3)+\cdots+c(n_1,a_1,K)=h^*(n_1)\)

定理2：A*完备性

• 搜索树中的分支数量是有限的，即每个结点的后继结点数量是有限的
• 单步代价的下界是一个正数
• 启发函数有下界

定理3：可容 \(\Rightarrow\) 最优

证：假设A*找到的终点为\(n\)，\(\forall n'\in\)边缘节点，\(f(n)\leqslant f(n')\)

\(\therefore f(n)=g(n)+h(n)=g(n)\leqslant f(n')=g(n')+h(n')\leqslant g(n')+h^*(n')\)

\(\therefore\)为最短路