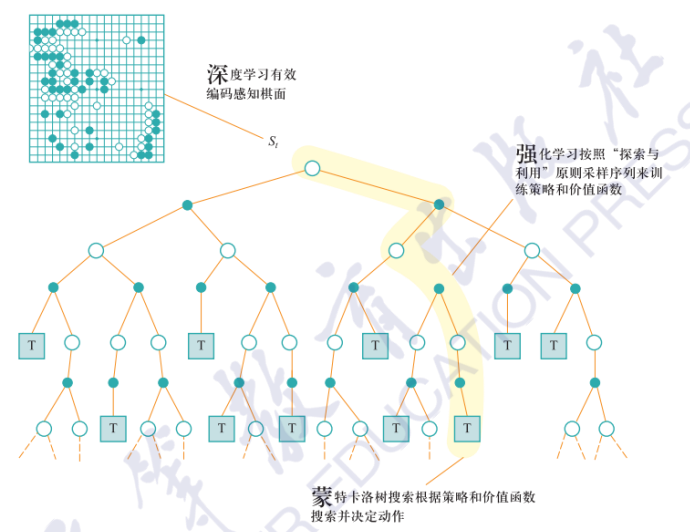
强化学习方法

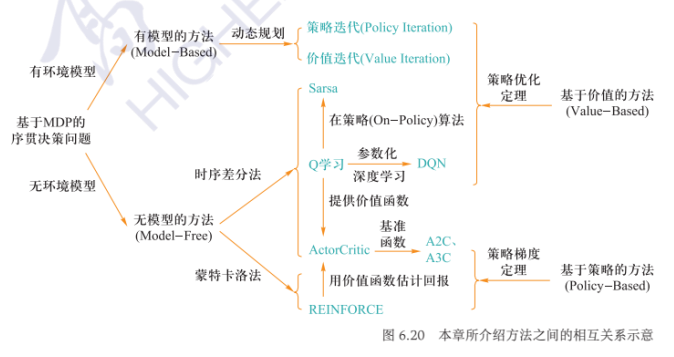
思路：从一个任意的策略开始，首先 计算该策略下的价值函数(或动作一价值函数)，然后根据价值函数调整、改进策略使其更优，不断迭代这个过程，直到策略收敛

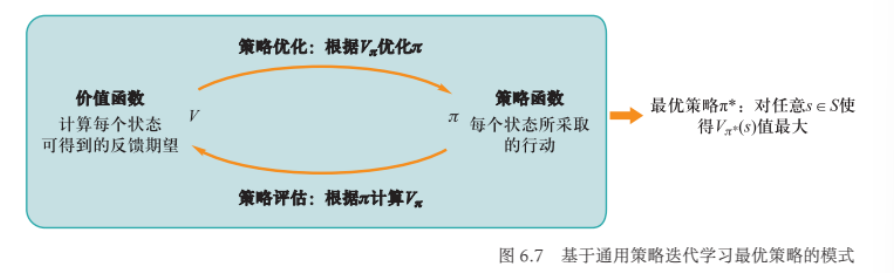
• 策略评估：通过策略计算价值函数
• 策略优化：通过价值函数优化策略
• 策略迭代：策略评估和策略优化交替进行的强化学习求解方法

策略优化定理：\(\forall s\in S,q_\pi(s,\pi'(s))\geqslant q_\pi(s,\pi(s))\Rightarrow\forall s\in S,V_\pi'(s)\geqslant V_\pi(s)\)

例：

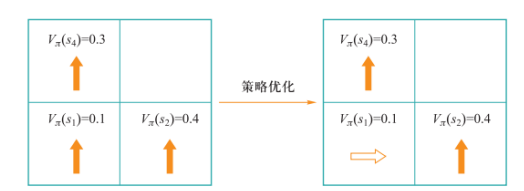$$ q_\pi(s_1,\uparrow)=\sum_{s'\in S}P(s'|s_1,\uparrow)[R(s_1,\uparrow,s')+\gamma V_\pi(s')]=1\times(0+0.99+0.3)\approx0.3 $$

\[ q_\pi(s_1,\rightarrow)=\sum_{s'\in S}P(s'|s_1,\rightarrow)[R(s_1,\rightarrow,s')+\gamma V_\pi(s')]=1\times(0+0.99+0.4)\approx0.4 \]

故将\(\pi=\uparrow\)优化为\(\pi^*=\rightarrow\).

策略评估方法：根据策略\(\pi\)来计算相应的价值函数\(V_\pi\)或动作-价值函数\(q_\pi\)

• 方法
  • DP
  • MC
  • 时序差分
• 本质：求解贝尔曼方程组
  • 高斯消元
  • Gauss-Seidel迭代

DP：

• 状态转移方程： $$ V_\pi(s)\leftarrow\sum_{a\in A}\pi(s,a)\sum_{s'\in S}P(s'|s,a)[R(s,a,s')+\gamma V_\pi(s')] $$
• 算法：

MC：大数定理指出，对于独立同分布的样本数据，当样本足够大时，样本平均值向期望值收敛

• 给定状态\(s\)，从该状态出发不断采样后续状态，得到不同的状态序列，通过这些采样序列来分别计算状态\(s\)的回报值，将这些回报值的均值作为对状态\(s\)的价值函数的估计
• 算法：

时序差分：蒙特卡洛方法和动态规划方法的有机结合

• 更新公式： $$ V_\pi(s)\leftarrow V_\pi(s)+a[R+\gamma V_\pi(s')-V_\pi(s)] $$
• 算法：

Q-Learning：直接记录和更新动作-价值函数\(q_n\)而不是价值函数\(V_\pi\)

• 更新公式： $$ q_\pi(s,a)\leftarrow q_\pi(s,a)+\alpha[R+\gamma\max a'q_\pi(s',a')-q_\pi(s,a)] $$
• 算法：

\(\epsilon\)-greedy：为智能体改变固有策略添加一个探索的动力

• 策略：

\[ \epsilon-\text{greedy}(s)=\left\{\begin{array}{ll}\mathop{\arg\!\max}_aq(s,a),&P=1-\epsilon,\\\text{random}\ a\in A,&P=\epsilon\end{array}\right. \]

• 算法：

参数化\(Q\)-learning：用一个回归模型拟合\(q_\pi\)函数

如果使用深度神经网络来拟合动作-价值函数则称为deep-Q learning

问题：

• 采样不足
• 难以收敛

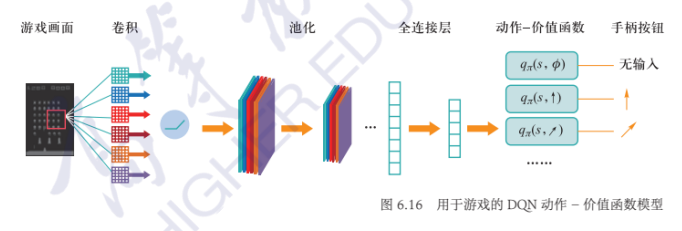
DQN：

• 损失函数： $$ L(\theta)=\dfrac{1}{2}[R+\gamma\max_aq_\pi(s',a';\theta^--q_\pi(s,a';\theta))]^2 $$
• 网络结构： 策略梯度定理：策略函数\(\pi_\theta(s,a)\)在状态s下选择动作a的概率，评估\(J(\theta):=V_{\pi_\theta}(s_0)\)
• 梯度： $$ \nabla_\theta J(\theta)=\nabla_\theta\sum_s\mu_{\pi_\theta}(s)\sum_aq_{\pi_\theta}(s,a)\pi_\theta(s,a)\propto\sum_s\mu_{\pi_\theta}(s)\sum_aq_{\pi_\theta}(s,a)\nabla_\theta\pi_\theta(s,a) $$

其中\(\mu_{\pi_\theta}(s)\)称为\(\pi_\theta\)的策略分布，持续问题中\(\mu_{\pi_\theta}(s)\)为算法在策略\(\pi_\theta\)安排下从\(s_0\)出发经过无限多步后位于状态\(s\)的概率；分段问题中\(\mu_{\pi_\theta}(s)\)为归一化后算法从\(s_0\)出发访问\(s\)次数的期望。

基于MC的策略梯度法：

• 公式： $$ \nabla_\theta J(\theta)\propto \mathbb E_{s,a\sim\pi}[q_{\pi_\theta}(s,a)\nabla_\theta\ln\pi_\theta(s,a)]=\mathbb E_{s,a,J(s,a)\sim\pi}[G_t\nabla_\theta\ln\pi_\theta(s,a)] $$

• REINFORCE算法

• Actor-Critic算法：从时序差分角度进行设计，时序差分与蒙特卡洛采样的核心差别在于使用下一时刻状态的价值函数来估计当前状态的价值函数，而不是使用整个片段的反馈值

  • 使用\(R+\gamma V_{\pi_\theta}(s')\)代替\(G\)

应用：AlphaGo